1.2.2 Износ Втулки
На рисунке 8 представлен график половинной функции Лапласа.
Рисунок 8 - Половинная
функция Лапласа
Рассчитаю интегральную функцию F(t) нормального распределения для Х7 (износ втулки), задавшись Тср=6000 час., =3,53, определю аргумент функции Лапласа и занесу данные в табл. 3.
Таблица 5 - Сводная таблица расчета интегральной функции нормального распределения
t103, час. |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
Х |
-0,43 |
-0,27 |
-0,12 |
0,04 |
0,19 |
0,35 |
0,5 |
Ф(х) |
-1 |
-0,44 |
-0,02 |
0,26 |
0,48 |
0,62 |
0,72 |
F(t) |
0 |
0,28 |
0,49 |
0,63 |
0,74 |
0,81 |
0,86 |
На основе расчетных данных таблицы 6 построю график нормального распределения (рисунок 9).
Процедура моделирования аналогична рассмотренной выше. Полученную выборку 86 занесу в таблицу 6.
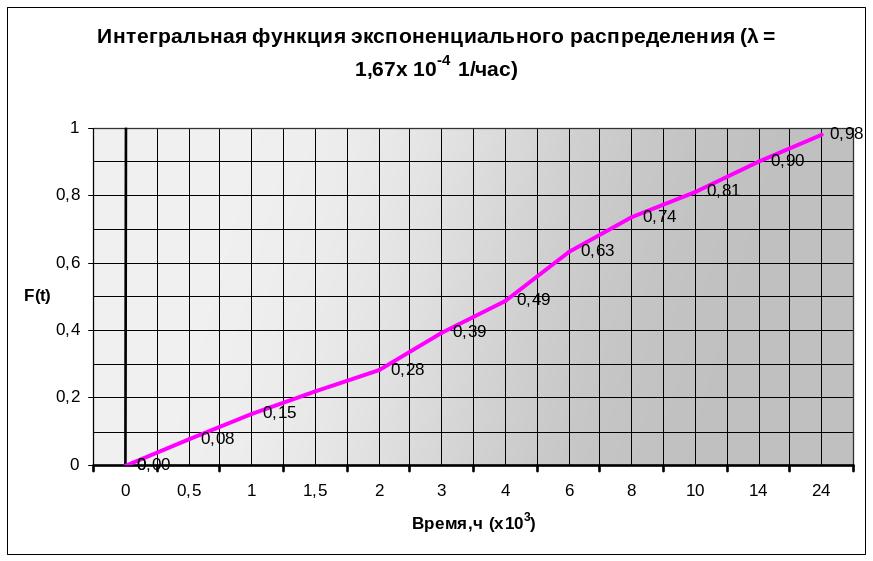
Рисунок 9 - Интегральная функция
нормального распределения
Полный коэффициент
отказа элемента системы
Таблица 6- Временная выборка из 86 элементов
m n |
Количество элементов |
t0 |
tобщ |
t0/tобщ |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||
Количество реализаций |
1 |
0,67 (2,33) |
1,5 (1,5) |
8,6 |
3,5 |
2,15 (0,85) |
7,6 |
13 |
4 |
4,68 |
41,02 |
0,114 |
2 |
2,2 (0,8) |
1,77 (1,33) |
5 |
8,9 |
5,4 |
4 |
21 |
8 |
2,13 |
56,27 |
0,038 |
|
3 |
15 |
5,3 |
1,8 (1,2) |
4,7 |
1,35 (1,65) |
3,5 |
5 |
7 |
2,85 |
43,65 |
0,065 |
|
4 |
4 |
6,5 |
4,3 |
5,4 |
2,5 (0,5) |
6 |
8 |
3 |
0,5 |
39,7 |
0,013 |
|
5 |
8,7 |
0,75 (2,25) |
10 |
1,88 (1,12) |
3,5 |
6,9 |
6 |
5 |
3,37 |
42,73 |
0,079 |
|
6 |
3 |
2 (1) |
11 |
9 |
6,9 |
8,3 |
3 |
9 |
1 |
52,2 |
0,019 |
|
Итого:0,328 |
||||||||||||
1.2.3. Износ набивки
На рисунке 10 представлен график половинной функции Лапласа.
Рисунок 10 -
Половинная функция Лапласа
Рассчитаю интегральную функцию F(t) нормального распределения для Х8 (износ набивки), задавшись Тср=5000 час., =2,58, определю аргумент функции Лапласа и занесу данные в табл. 7.
Таблица 7 - Сводная таблица расчета интегральной функции нормального распределения
t103, час. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Х |
-0,27 |
-0,19 |
-0,12 |
-0,04 |
0,0387 |
0,12 |
0,19 |
0,27 |
0,35 |
Ф(х) |
-0,64 |
-0,34 |
-0,1 |
0,1 |
0,26 |
0,4 |
0,5 |
0,6 |
0,66 |
F(t) |
0,18 |
0,33 |
0,45 |
0,55 |
0,63 |
0,7 |
0,75 |
0,8 |
0,83 |
На основе расчетных данных таблицы 7 построю график нормального распределения (рисунок 11).
Процедура моделирования аналогична рассмотренной выше. Полученную выборку 86 занесу в таблицу 8.
Рисунок 11 - Интегральная функция
нормального распределения
Полный коэффициент
отказа элемента системы
Таблица 8- Временная выборка из 86 элементов
m n |
Количество элементов |
t0 |
tобщ |
t0/tобщ |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||
Количество реализаций |
1 |
0,5 (2) |
1,75 (0,75) |
3 |
8 |
4 |
6,5 |
14,5 |
2 (0,5) |
3,25 |
40,25 |
0,081 |
2 |
4,5 |
6,5 |
1,7 (0,8) |
3 |
8,5 |
2 (0,5) |
5 |
3,6 |
1,3 |
34,8 |
0,037 |
|
3 |
8 |
12 |
2 (0,5) |
2,5 |
7,75 |
1 (1,5) |
2,5 |
15 |
2 |
50,75 |
0,039 |
|
4 |
11,5 |
8 |
3 |
1,25 (1,25) |
4,15 |
5,25 |
3,1 |
2,9 |
1,25 |
39,15 |
0,032 |
|
5 |
3,75 |
9 |
15 |
6 |
2,25 (0,25) |
7,75 |
1,78 (0,72) |
3,7 |
0,97 |
49,23 |
0,020 |
|
6 |
9,6 |
5 |
2,5 |
10 |
3 |
7 |
12 |
6,5 |
0 |
55,6 |
0 |
|
Итого:0,209 |
||||||||||||