2. Разработка отверстий

Приму среднюю наработку на отказ устройства при разработки отверстий Т_ср=250000 часов.

F(100000)=0,33	F(700000)=0,94
F(300000)=0,7	F(800000)=0,96
F(500000)=0,86	F(900000)=0,97
F(600000)=0,91	F(1000000)=0,98

По расчетным данным построю интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 34 раза больше Т_ср. На оси ординат — значение функции F(t).

Рисунок 5 - Интегральная функция экспоненциального распределения

Таблица 2 - Временная выборка из шести реализаций для восьми элементов t10³ час

m n		Количество элементов								t0	tобщ	t0/tобщ
		1	2	3	4	5	6	7	8
Количество реализаций	1	400	425	115 (10)	365	689	900	125	110 (15)	25	3129	0,0080
	2	230	315	50 (75)	528	426	513	675	108 (17)	92	2845	0,0323
	3	575	675	364	635	135	246	178	213	0	3021	0
	4	125	110 (15)	689	100 (25)	467	328	529	115 (10)	50	2463	0,0203
	5	300	305	755	125	545	289	635	500	0	3454	0
	6	35 (90)	514	213	458	135	400	518	120 (5)	95	2393	0,0397
Итого: 0,1003

Расчеты проведу аналогично п 1.1.1

Вероятность отказа элемента системы Х₁

1.2 Моделирование постепенных отказов

1.2.1 Износ Гаек

Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:

(1.6)

где  - среднеквадратичное отклонение; a — математическое ожидание.

Для того, чтобы не рассчитывать интеграл, воспользуюсь половинной функцией Лапласа и с ее помощью рассчитаю нормальный закон распределения по формуле:

(1.7)

где Ф(х) - половинная функция Лапласа; х=(t - T_ср)/, где

х - аргумент функции Лапласа;

t - время функционирования;

Т_ср - средняя наработка на отказ;

 - среднеквадратичное отклонение.

На рисунке 6 представлен график половинной функции Лапласа.

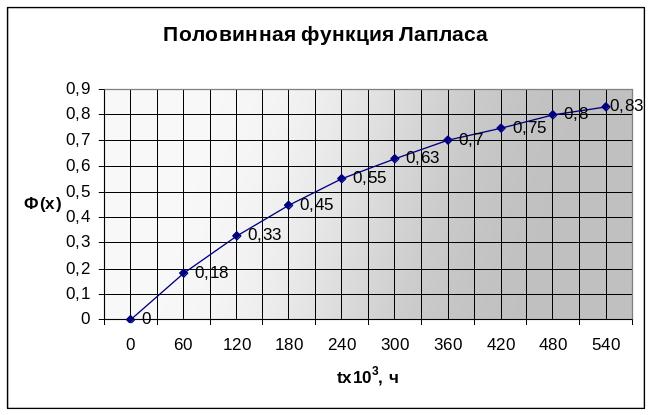
Рисунок 6 - Половинная функция Лапласа

Рассчитаю интегральную функцию F(t) нормального распределения для Х₃ (износ гаек), задавшись Т_ср=300000 час., =154,92, определю аргумент функции Лапласа и занесу данные в табл. 3.

Таблица 3 - Сводная таблица расчета интегральной функции нормального распределения

t103, час.	60	120	180	240	300	360	420	480	540
Х	-14,7	-10,1	-5,42	-0,77	3,873	8,52	13,2	17,8	22,5
Ф(х)	-0,64	-0,34	-0,1	0,1	0,26	0,4	0,5	0,6	0,66
F(t)	0,18	0,33	0,45	0,55	0,63	0,7	0,75	0,8	0,83

На основе расчетных данных таблицы 4 построю график нормального распределения (рисунок 7).

Процедура моделирования аналогична рассмотренной выше. Полученную выборку 86 занесу в таблицу 4.

Полученные в таблице 4 значения сравню с Т_ср, т. к. меня интересует характеристика системы в первый период эксплуатации. В тех случаях, если t₀<T_ср, найду нерабочее время t₀ элемента системы Х₃ по формуле . Полученное время указано в скобках в таблице 4. Затем, просуммировав время t₀ по реализации, беру отношение t₀ к суммарному времени функционирования элемента системы Х₃ в этой реализации . Вероятность отказа элемента системы Х₃ в данной реализации определю по формуле (1.4):

Рисунок 7 - Интегральная функция нормального распределения

Полный коэффициент отказа элемента системы рассчитывается как

Его численное значение

Аналогично промоделирую для остальных гаек Х₄, Х₅, Х₆. В данном примере получены такие значения:

Таблица 4- Временная выборка из 86 элементов

m n		Количество элементов								t0	tобщ	t0/tобщ
		1	2	3	4	5	6	7	8
Количество реализаций	1	800	115 (35)	158	108 (42)	445	220	615	30 (120)	197	2491	0,079
	2	650	740	450	520	160	280	568	90 (60)	60	3458	0,017
	3	340	870	240	145 (5)	130 (20)	50 (100)	1100	980	125	3855	0,032
	4	590	1000	630	235	106 (44)	580	360	270	44	3771	0,012
	5	150	139 (11)	890	30 (120)	650	430	670	490	131	3449	0,038
	6	460	200	350	870	190	540	708	150	0	3468	0
Итого: 0,179