3.1 Моделирование внезапных отказов

3.1.1. Заклинивание плунжера

Построю интегральную функцию экспоненциального распределения:

где  — интенсивность отказов.

Интенсивность отказов рассчитывается по формуле: 1/час

где Т_ср — среднее время наработки на отказ.

Приму среднюю наработку на отказ устройства при заклинивании клапана Т_ср=220000 часов.

F(55000)=0,22	F(550000)=0,92
F(110000)=0,39	F(660000)=0,95
F(330000)=0,78	F(770000)=0,97
F(440000)=0,86	F(880000)=0,98

По расчетным данным построю интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 34 раза больше Т_ср. На оси ординат — значение функции F(t).

Рисунок 4 - Интегральная функция экспоненциального распределения

Таблица 1 - Временная выборка из шести реализаций для семи элементов t10³ час

m n		Количество элементов							t0	tобщ	t0/tобщ
		1	2	3	4	5	6	7
Количество реализаций	1	224	115	175	325	76 (34)	109(1)	226	35	1250	0,028
	2	378	216	100 (10)	198	120	118	279	10	1409	0,007
	3	85 (25)	27,5 (82,5)	110	374	65 (45)	110	115	152,5	886,5	0,172
	4	50 (60)	294	53 (57)	275	467	50 (60)	345	177	1534	0,115
	5	415	57 (53)	523	67 (43)	147	628	220	96	2057	0,047
	6	83 (27)	165	353	110	206	75 (35)	30 (80)	142	1022	0,139
Итого: 0,508

Далее временные значения ti, приведенные в таблице 1, сравню с Тср/2 = 110000, поскольку меня интересует поведение системы в первый полупериод эксплуатации. Затем получу время t0 нерабочего состояния элемента системы Х1, выбирая лишь те случаи, когда ti<Тср/2. Расчет произведу по формуле

Полученное значение t0 занесу в таблицу 1, указав его в скобках, затем суммирую нерабочее время в единичной реализации t0 и беру отношение к сумме общего времени tобщ работы элемента в этой реализации. На основе полученных значений определю вероятность отказа элемента системы Х1 для данной реализации по формуле:

)

и так для каждой реализации.

Вероятность отказа элемента системы Х₁ является средним арифметическим этих значений:

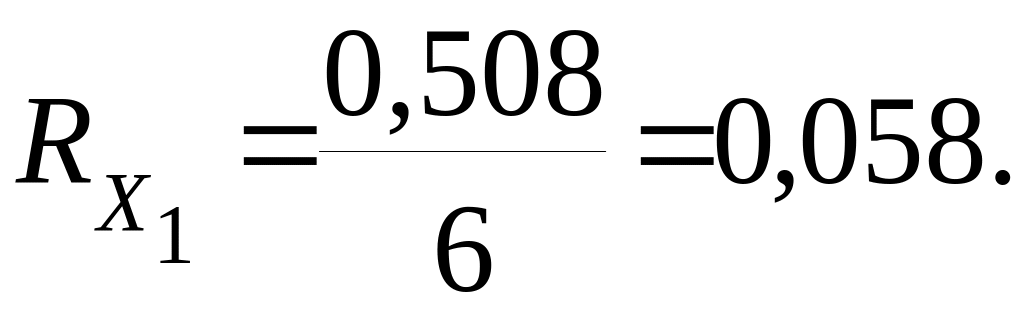
2. Поломка пружины.

Приму среднюю наработку на отказ устройства при разработки отверстий Т_ср=250000 часов.

F(100000)=0,33	F(700000)=0,94
F(300000)=0,7	F(800000)=0,96
F(500000)=0,86	F(900000)=0,97
F(600000)=0,91	F(1000000)=0,98

По расчетным данным построю интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 34 раза больше Т_ср. На оси ординат — значение функции F(t).

Рисунок 5 - Интегральная функция экспоненциального распределения

Таблица 2 - Временная выборка из шести реализаций для семи элементов t10³ час

m n		Количество элементов							t0	tобщ	t0/tобщ
		1	2	3	4	5	6	7
Количество реализаций	1	367	525	417	115 (10)	50(75)	100 (25)	125	35	1699	0,021
	2	319	429	60 (85)	615	456	326	715	85	2920	0,029
	3	120 (5)	475	989	755	927	386	178	5	3830	0,001
	4	125	110 (15)	596	100 (25)	703	383	819	40	2836	0,014
	5	100 (25)	205	629	125	45 (80)	289	784	105	2177	0,048
	6	35 (90)	514	213	358	135	400	518	90	2173	0,041
Итого: 0,155

Расчеты проведу аналогично п 3.1.1

Вероятность отказа элемента системы Х₂