3 Потенциальные кривые взаимодействия частиц

Потенциальная кривая это графическое представление зависимости потенциальной энергии взаимодействия двух частиц от расстояния между ними. Частицы считаются сферическими и одинаковыми по размеру. В расчет энергии входит кратчайшее расстояние между поверхностями этих частиц. В этой задаче фиксированными являются потенциал поверхности, размер и химическая природа частиц, которая, в свою очередь определяет константу их молекулярного притяжения. Последняя не может быть надежно вычислена и потому здесь она задается по некоторому правилу. Варьируемым параметром задачи является концентрация c индифферентного электролита, определяющая, согласно теории устойчивости коллоидов (ДЛФО), агрегативную устойчивость дисперсной системы и критерии этой устойчивости – значение максимума (потенциального барьера) и минимума (потенциальной ямы) потенциала взаимодействия в сравнении с кинетической энергией броуновских столкновений частиц kT (k=1,38^.10^-21 Дж/К, T – темпреартура). Ориентиром при выборе (назначении) концентрации электролита является его критическая концентрация c_c– минимальная концентрация, при которой происходит быстрая, необратимая коагуляция дисперсной системы – необратимое слипание частиц при каждом их столкновении. При этой концентрации потенциальный барьер равен нулю.

После вычисления необходимых констант в таблице 3.1 вычисляется зависимость энергии взаимодействия частиц U от расстояния h и по ней строится график 3.1.

Обозначения, наименования, размерности величин и формулы для их вычисления*

Приведенный размер (радиус) частиц - 1/, м. Приведенные константы, энергии и силы – это соответствующие величины, относящиеся к частицам приведенного размера.

A' - константа притяжения дисперсной фазы, Дж Задана как 10^-24

A - константа притяжения частиц, Дж/м …………………………. A= aA'

с - концентрации электролита

 - функция потенциала поверхности =[1- exp(-z /2)]/[1+exp(-z /2)]

B'' - универсальная константа отталкивания (частиц приведенного размера a=1/ при =1)

B''=32_o(RT/zF)²

B' - приведенная константа отталкивания , Дж/м ………………. B'=B'' ²

B - константа отталкивания частиц заданного размера, Дж ……..B=aB'

æ_c - критическая величина параметра Дебая , 1/м …………………æ_c=B'/eA'

b - константа Дебая раствора симметричного электролита b=zF(2/_o RT)^1/2

æ - параметр Дебая раствора симметричного электролита, 1/м æ=bc^1/2

c_c - критическая концентрация симметричного электролита, моль/л c_c=( æ_c/b)²

h - расстояние между поверхностями частиц, м

U_e - энергия электростатического отталкивания частиц, Дж U_e=Bexp(-æh)

U_m - энергия молекулярного притяжения частиц, Дж ………….. U_m= - A/h

U - энергия взаимодействия частиц U=U_e + U_m , Дж U=Bexp(-æh) - A/h

U'- приведенная энергия частиц, Дж/м …………………U '=B'exp(-æ h) - A'/h

F- сила взаимодействия частиц, Н ………………………F= æBexp(-æh) - A/h²

F'- приведенная сила взаимодействия частиц, Н/м F '= æB'exp(-æh) - A'/h²

* Смотри так же обозначения к предыдущим темам.

Задание: Рассчитать и построить потенциальные кривые взаимодействия частиц при двух концентрациях электролита: первая - критическая, вторая – в 4 раза меньше критической. Дать заключение об устойчивости или характере коагуляции.

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

5 Плотность дисперсной фазы кг/м³ 3140

8 Потенциал поверхности мВ -46

9 Размер частиц м 2,07^.10^-6

Константа притяжения дисперсной фазы Дж 3,14^.10^-21

Константы:

Число Фарадея, Кл/кэкв 9,65^.10⁷

Газовая постоянная Дж/К ^. кмоль 8310

Диэлектрическая постоянная Ф/м 8,85^.10^-12

Диэлектрическая проницаемость среды 81

Температура К 293

Расчет констант взаимодействия:

Универсальная константа Дебая для раствора 3,27^.10⁹

Безразмерный потенциал противоионов 1,84

Универсальная константа отталкивания Дж/м 1,46^.10^-11

Функция потенциала поверхности -0,43

Приведенная константа отталкивания Дж/м 2,7^.10^-12

Критическое значение параметра Дебая раствора 1/м 3,16^.10⁸

Критическая концентрация электролита моль/литр 9,36^.10^-3

Константа отталкивания частиц Дж 1,75^.10^-17

Константа притяжения частиц Дж.м 2,04^.10^-26

Таблица 3.1 - Расчет функций взаимодействия:

шаг капа, м^-1 B, Дж A, Дж.м порядок критическая концентрация, моль/л 0,00936

0,5 1,58.10⁸ 1,75.10^-17 2,04.10^-26 -17 1.10¹⁷ текущие концентрации электролита, м/л

0,00234 0,00234 0,00936

капа*h	h, м	Ue, Дж	Um, Дж	U, Дж	U*1017, Дж	h, нм	U*1017, Дж	U*1017, Дж
0,5	3,16.10-9	1,06.10-17	-6,46.10-18	4,19.10-18	0,419	1,58	0,0755	-0,227
1,0	6,33.10-9	6,46.10-18	-3,23.10-18	3,23.10-18	0,323	3,16	0,4188	0,000
1,5	9,49.10-9	3,92.10-18	-2,15.10-18	1,76.10-18	0,176	4,75	0,3986	-0,039
2,0	1,27.10-8	2,37.10-18	-1,61.10-18	7,61.10-19	0,076	6,33	0,3228	-0,085
2,5	1,58.10-8	1,44.10-18	-1,29.10-18	1,49.10-19	0,015	7,91	0,2445	-0,114
3,0	1,90.10-8	8,74.10-19	-1,08.10-18	-2,02.10-19	-0,020	9,49	0,1764	-0,128
3,5	2,21.10-8	5,30.10-19	-9,22.10-19	-3,92.10-19	-0,039	11,07	0,1205	-0,131
4,0	2,53.10-8	3,21.10-19	-8,07.10-19	-4,86.10-19	-0,049	12,66	0,0761	-0,129
4,5	2,85.10-8	1,95.10-19	-7,17.10-19	-5,22.10-19	-0,052	14,24	0,0415	-0,124
5,0	3,16.10-8	1,18.10-19	-6,46.10-19	-5,27.10-19	-0,053	15,82	0,0149	-0,117
5,5	3,48.10-8	7,17.10-20	-5,87.10-19	-5,15.10-19	-0,052	17,40	-0,005	-0,110
6,0	3,80.10-8	4,35.10-20	-5,38.10-19	-4,94.10-19	-0,049	18,98	-0,02	-0,103
6,5	4,11.10-8	2,64.10-20	-4,97.10-19	-4,70.10-19	-0,047	20,57	-0,031	-0,097
7,0	4,43.10-8	1,60.10-20	-4,61.10-19	-4,45.10-19	-0,045	22,15	-0,039	-0,091
7,5	4,75.10-8	9,71.10-21	-4,30.10-19	-4,21.10-19	-0,042	23,73	-0,045	-0,085
8,0	5,06.10-8	5,89.10-21	-4,03.10-19	-3,98.10-19	-0,040	25,31	-0,049	-0,080

Примечание: Для автоматического построения графиков на рисунке 3.1 использованы последние три столбца таблицы 3.1 (выделены курсивом). Здесь значения функций при разных концентрациях электролита приведены к одинаковой шкале расстояния между частицами и могут не совпадать со шкалой расстояний во втором столбце таблицы. Вручную графики стоятся по данным столбцов 2 (h, м) и 5 (U, Дж).

2

1

Рисунок 3.1 - Потенциальные кривые взаимодействия частиц при концентрации электролита: 1 –0,00936 моль/л (критическая), 2 –0,00234 моль/л.

Вывод: При концентрации электролита 0,0094 моль/л U_max=0, поэтому происходит быстрая необратимая коагуляция.

При концентрации 0,0023 моль/л U_max≈0,42.10^-17 Дж, U_min≈ -0,05.10^-17 Дж, что много больше kT, равного 4^.10^-21 Дж, поэтому происходит неконтактная обратимая коагуляция.

4 ЭКСТРЕМУМЫ ФУНКЦИЙ ВЗАИМОДЕЙСТВИЯ

В большинстве случаев для суждения о поведении дисперсной системы нет необходимости рассчитывать всю потенциальную или силовую функцию взаимодействия частиц и строить соответствующий график (кривую). Для этого достаточно знание экстремумов функции взаимодействия – максимума (потенциального или силового барьера) и минимума (потенциальной или силовой ямы) и их координат на оси расстояний.

Экстремумы потенциальной энергии определяют поведение дисперсной системы, если частицы взаимодействуют между собой путем их тепловых (броуновских) столкновений. Такой тип взаимодействия присущ частицам коллоидных размеров (порядка 10^-7 м и менее). Результат столкновения зависит в этом случае от соотношения экстремумов потенциальной функции и средней энергии тепловых соударений (kT).

В суспензия и эмульсиях (размер частиц порядка 10^-6 м и более) интенсивность их броуновского движения (среднеквадратичного смещения) мала, поэтому мала вероятность теплового преодоления потенциального барьера и ямы. Поведение частиц в этом случае определяется величиной внешней силы, действующей на частицы. Это может быть сила тяжести, сдавливающая частицы в осадке, гидродинамическая сила, разрушающая флокулы из слипшихся частиц в потоке и др. Результат воздействия внешней силы зависит от соотношения величины этой силы и экстремальных значений силовой функции взаимодействия частиц - максимума и минимума силовой кривой взаимодействия частиц. Очевидно, что силовой барьер (максимум силовой кривой) будет преодолен и частицы необратимо слипнутся, если внешняя сила будет больше силового барьера. При действии разрывающего усилия на слипшиеся частицы они будут разъединены, если разрывающее усилие превысит наибольшую силу притяжения частиц – минимум силовой кривой.

Обозначения, наименования, размерности величин и формулы для их вычисления

h_e - координата экстремума по оси расстояний, м

h_max - то же в случае максимума, м

h_min - то же в случае минимума, м

x - аргумент экспоненциально-степенного (ЭС) уравнения ……………….x= æh

Y - экспоненциально-степенная (ЭС) функция ………………………………Y=x^pe^-x

Y_p - ее частный вид при фиксированном показателе p

æ/æ_c - отношение текущего и критического значений параметра Дебая

ЭС уравнение (общий вид) ……………………………………………x^pe^-x=(p-1)(æ/æ_c)/e

ЭС уравнение для силовой функции взаимодействия (p=3) x³e^-x=(2/e)(æ/æ_c)

ЭС уравнение для энергетической функции взаимодействия (p=2) x²e^-x=(1/e)(æ/æ_c)

Так как уравнения такого вида аналитически не решаются, то ниже (табл. 4.1 и рисунок 4.1) приведены таблицы и графики функции Y при р=3 и p=2, предназначенные для табличного или графического нахождения корней x_e приведенных уравнений. Для этого по известным (заданным) значениям æ и æ_c вычисляется значение правой части нужного уравнения и по соответствующему графику (рисунок 4.1) или таблице (4.1) находятся корни x_e уравнения – значения аргументов x , при которых значение правой части уравнения равно значению функции x^pe^-x.

x_e - корни показательно-степенного уравнения

Корней два.

x₁ - первый корень ЭС уравнени …….…………………………………….x₁= æh₁

x₂ - второй корень ЭС уравнения (x₂>x₁) ……………………………………x₂= æh₂

Первый корень (меньший по величине) соответствует максимуму, а второй - минимуму исследуемой функции. По значениям корней вычисляются значение расстояний h₁=x₁/æ и h₂= x₂/æ, на которых исследуемая функция имеет максимум и минимум соответственно.

Значения максимума и минимума функции вычисляется по приведенным ниже уравнениям

U'_xtr - экстремум приведенной энергии, Дж/м ……………………....U '_xtr=B'(1-xe)e^{- xe}

U'_max - максимум приведенной энергии, Дж/м ………………………U '_max=B'(1-x₁)e^{- x1}

U'_min - минумум приведенной энергии, Дж/м ……………………….U ' _min=B'(1-x₂)e^{- x2}

F'_xtr - экстремум приведенной силы, Н/м …………………… F '_xtr=(1/2) æ B'(2-xe)e^{- xe}

F'_max - максимум приведенной силы, Дж ……………………. F '_max=(1/2) æ B'(2-x₁)e^{- x1}

F'_min - минимум приведенной силы, Дж ……………………... F '_min=(1/2) æ B'(2-x₂)e^{- x2}

U_xtr - экстремумы энергии взаимодействия частиц радиусом a, Дж U_xtr=aU '_xtr

F_xtr - экстремумы силы взаимодействия частиц радиусом a , Н F_xtr=aF '_xtr

Задание: Найти экстремальные значения энергии и силы взаимодействия частиц и их координаты на оси расстояний

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

9 Размер частиц м 2,07^.10E^-6

Приведенная константа отталкивания Дж 1,75^.10^-17

Константа притяжения дисперсн. фазы Дж*м 3,14^.10^-21

Концентрация электролита моль/л 9,36^.10^-3

Расчет констант:

Параметр Дебая раствора 1/м 3,16^.10⁸

Отношение (капа/капа критическое) 1

Расчет экстремумов энергии:

Значение правой части ЭС уравнения 0,368

Координата максимума в толщинах ДЭС 1

Потенциальный барьер Дж 1,15^.10^-24

Координата максимума м 3,16^.10^-9

Координата минимума в толщинах ДЭС 3,513

Потенциальная яма Дж -1,3^.10^-18

Координата минимума м 1,11^.10^-8

Расчет экстремумов силы:

Значение правой части ЭС уравнения 0,736

Координата максимума в толщинах ДЭС 1,477

Силовой барьер Н 3,31^.10^-10

Координата максимума м 4,67^.10^-9

Координата минимума в толщинах ДЭС 5,323

Силовая яма Н -4,5^.10^-11

Координата минимума м 1,68^.10^-8

Координаты экстремальных точек должны соответствовать потенциальным кривым (Рисунок 3.1)

Таблица 4.1 - Функции Y =x^p.e^-x для нахождения экстремумов

потенциала и силы взаимодействия частиц

x	x2 .e-x	x3 .e-x	x	x2 .e-x	x3 .e-x
0	0	0	3,6	0,354115	1,274816
0,2	0,032749	0,00655	3,8	0,323034	1,227529
0,4	0,107251	0,0429	4	0,29305	1,172201
0,6	0,197572	0,118543	4,2	0,264522	1,110992
0,8	0,287571	0,230056	4,4	0,237689	1,045833
1	0,367879	0,367879	4,6	0,212697	0,978405
1,2	0,43372	0,520464	4,8	0,189613	0,910144
1,4	0,48333	0,676662	5	0,168449	0,842243
1,6	0,516855	0,826968	5,2	0,149168	0,775673
1,8	0,535568	0,964023	5,4	0,131704	0,711199
2	0,541341	1,082682	5,6	0,115965	0,649404
2,2	0,536287	1,179832	5,8	0,101847	0,590712
2,4	0,522535	1,254085	6	0,089235	0,53541
2,6	0,502089	1,305432	6,2	0,078011	0,48367
2,8	0,476751	1,334902	6,4	0,068057	0,435567
3	0,448084	1,344251	6,6	0,059258	0,3911
3,2	0,417405	1,335696	6,8	0,051501	0,350207
3,4	0,385795	1,311703	7	0,044682	0,312776

1

2

Рисунок 4.1 - Графики функций Y =x^p.e^-x для нахождения экстремумов:

1 – потенциала (p=2) и 2 - силы взаимодействия частиц (p=3).

5 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ.

Молекулярно-кинетические свойства это свойства, обусловленные движением частиц. Основная особенность дисперсных систем в том, что в них сопоставимы по интенсивности два разных типа движения частиц – регулярное и хаотичное. Первое обусловлено действием на частицы определенной силы и потому полностью предсказуемо и характеризуется скоростью движения. Примером является оседание частиц дисперсной фазы под действием силы тяжести (седиментация). Хаотичное движение вызывается случайными импульсами, которые частица получает от столкновений с другими участниками этого движения. Универсально по своей природе тепловое (броуновское) движение. В деталях оно непредсказуемо, но его среднестатистические характеристики имеют вполне определенное значение. Таковыми являются средняя кинетическая энергия kT теплового движения (k – постоянная Больцмана и T – температура по шкале Кельвина) и среднеквадратичное смещение частиц за произвольный промежуток времени. Макроскопическим проявлением теплового движения является диффузия – перенос компонента системы в направлении выравнивания его концентрации (в общем случае - химического потенциала). Интенсивность диффузии компонентов системы определяется их коэффициентами диффузии D.

Одновременное участие частиц в седиментации и диффузии ведет к установлению в сосуде со взвесью частиц седиментационно-диффузионного равновесия, при котором зависимость концентрации дисперсной фазы от высоты описывается законом распределения Больцмана. Только в коллоидных растворах, благодаря сопоставимости интенсивностей обоих типов движения, пространственный масштаб неоднородности распределения вещества по высоте доступен непосредственному наблюдению – различие концентраций заметно при высоте сосуда с раствором порядка сантиметров. В более грубых взвесях оно не может быть замечено, так как характерная высота изменения концентрации меньше размера частиц, т.е. они образуют осадок. В системах с молекулярным уровнем дисперсности (истинных растворах, газах) характеристическая высота составляет сотни и тысячи метров и потому может наблюдаться только в геологических масштабах, например в виде различной величины атмосферного давления на разных высотах над уровнем моря.

В коллоидах диффузно распределенная взвешенная часть вещества может равновесно сосуществовать с осадком на дне сосуда. В осадке концентрация максимальна и постоянна по высоте осадка. Важная для технологии задача заключается в определении условий образования осадка и доли вещества в осадке и диффузной взвеси.

Обозначения, наименования, размерности величин и формулы для их вычисления*

H - высота сосуда (взвеси), м

h - текущая высота (расстояние от дна сосуда), м

 - рецептурная концентрация (объемная доля во взвеси) дисперсной фазы

k - константа Больцмана, Дж/К

₀ – вязкость дисперсионной среды, Па.с

 - плотность дисперсной фазы, кг/м³

₀ – плотность дисперсионной среды, кг/м³

 = -₀

g - ускорение свободного падения, м/с² ……………………………...9,81

в - коэффициент сопротивления Стокса, Н.с/м ……………………….в=6₀a

u - скорость оседания частицы в поле сил тяжести, м/с u=mg/в, u=2ga²/9_o

D - коэффициент диффузии, м²/с …………………………………….. D=kT/в

x – среднеквадратичное смещение частицы за время t, м …………x = (2Dt)^1/2

m – масса частицы с поправкой на силу Архимеда, кг ………………m=v

v – объем частицы, м³

w - константа распределения, 1/м ……………………………………..w=mg/kT

wH - фактор распределения Больцмана ………………………………wH=mgH/kT

_h - концентрация дисперсной фазы (объемная доля) на высоте h  =₀.e^-wh

₀ - концентрация дисперсной фазы (объемная доля) на дне сосуда. Она подлежит

определению путем нормирования распределения Больцмана: f=wH(1- e^-wH)^-1

f - нормирующий множитель

_m – максимально возможная концентрация дисперсной фазы …… _m=1/(1+/a)³

Если f<_m то это означает, что осадока на дне нет, ₀=f и

по всей высоте сосуда действует закон Больцмана: ………….. _h= ₀e^-wh

Если f>_m то это означает, что на дне сосуда образуется осадок, ₀=_m ,

Распределение Больцмана ……………………………………_h=_m.e^-w(h-Hs)

действует только над осадком, т.е. при h>H_s . В осадке, т.е. при h< H_s _h=_m

H_s - высота слоя осадка находится из уравнения H = _mH_s+_mw^-1 [1- e^-w(H-Hs)]

* Смотри так же обозначения на по теме 1

Это уравнение материального баланса по дисперсной фазе, где H - общее количество вещества дисперсной фазы в дисперсной системе, _mH_s - количество вещества в осадке и _mw^-1 [1- e^-w(H-Hs)] = V- количество вещества во взвеси. Толщина защитной оболочки  при вычислении _m задается как толщина адсорбционного слоя молекул ПАВ на поверхности частиц (см. тему 1).

Уравнение можно решить методом последовательных приближений, приняв, в качестве нулевого приближения, что V=0 и тогда H_s =H/_m . Используя это значение H_s следует в первом приближении вычислить V, H_s =(H-V )/_m и _mH_s и сумму _mH_s + V . Если она с приемлемой точностью (порядка 1%), совпадает с полным колическтвом вещества в системе, то полученные величины можно принять как окончательные. В обратном случае следует проделать теже вычисления в следующем приближении, используя величину H_s последнего приближения.

В табличном процессоре Excel уравнение решается автоматически. Для этого оно приведено к виду, в котором левая сторона уравнения содержит только известные величины: (/_m)wH -1 = wH_s- e^-wH e^wHs. Решение проводится во вспомогательной таблице (в пособии оно не приводится) при нажатии* клавиши "Итерация". Эта клавиша видна только в электронном варианте задания. Результат – величина H_s вносится в ячейку "Высота осадка".

Задание: Вычислить скорость оседания и средний сдвиг частиц за секунду, фактор распределения Больцмана в поле сил тяжести, определить наличие осадка, его высоту, количество вещества в осадке и во взвеси.

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

1 Объемная доля дисперсной фазы 0,124

11 Высота сосуда м 0,228

5 Плотность дисп. фазы кг/м³ 3240

6 Плотность среды кг/м³ 929

4 Размер частиц м 1,70.10^-8

7 Вязкость среды Па.с 0,001175

Толщина защитной оболочки м 1,00.10^-9

Константы:

Константа Больцмана Дж/К 1,38.10^-23

Температура К 293

Ускорение свободного падения м/с² 9,81

Расчет констант распределения: Доля в осадке 0,7776

Скорость оседания м/с 1,19E-09

Коэффициент диффузии м2/с 1,07E-11

Среднеквадратичный сдвиг за секунду м 4,63E-06

Объем частицы м3 2,06E-23

Архимедова масса частицы кг 4,55E-20

Константа распределения mgH/kT 25,17

Эффективная доля дисперсной фазы во взвеси 1,79E-01

Объемная доля дисперсной фазы внутри осадка 0,6943

Решение уравнения сохранения вещества (нормироавние) 3,12

Наличие осадка Да

Высота осадка при полном оседании частиц м 0,040723

Количество вещества по условию задачи м 0,028272

Количество вещества во взвеси м 0,006289

Количество вещества в осадке м 0,021983

Сумма осадка и взвеси м 0,028272

Высота осадка м 0,031665

Константы уравнения материального баланса верно*

Больцмановский фактор осадка (верхний предел переменной) 4,50

Левая сторона уравнения 3,50

Таблица 5 .1 - Распределение дисперсной фазы по высоте

h, м	
0,228	0
0,213	0
0,197	0
0,182	0
0,167	0
0,152	0
0,137	0
0,121	0
0,106	9,95.10-5
0,091	0,0005
0,076	0,0028
0,061	0,0152
0,046	0,0812
0,030	0,4342
0,015	0,8424
0,000	0,8424

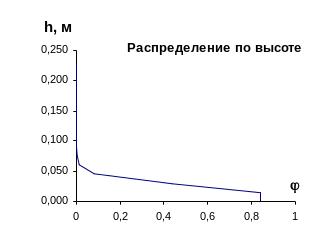
Рисунок 5.1 - Равновесное распределение дисперсной фазы по высоте в устойчивой дисперсной системе.

* Пометка "верно" вносится автоматически после решении уравнения материального баланса.

6 КИНЕТИКА КОАГУЛЯЦИИ И ФРАКТАЛЬНЫЕ СВОЙСТВА

Для технологии важен не только факт коагуляции дисперсной системы, но и скорость этого процесса, и его конечные результаты. Анализ потенциальных кривых дает ответ на вопрос о том будет ли происходить коагуляции и какова прочность сцепления частиц в коагуляте. Описание хода этого процесса во времени дает уравнение кинетики коагуляции Смолуховского – зависимость численной концентрации составных частиц от времени. Составные частицы это частицы, представляющие собой флокулу из нескольких слипшихся вместе индивидуальных частиц. Кинетической характеристикой процесса является в этом случае время половинной коагуляции – время, за которое численная концентрация частиц убывает в два раза. Для краткости его называют периодом полураспада.

Удобной величиной, характеризующей состояние коагулирующей системы в любой момент времени, является (в рамках кинетики Смолуховского) среднее число индивидуальных частиц в одной флокуле, равное отношению числа индивидуальных частиц до начала коагуляции к числу флокул в текущий момент времени. Эта величина имеет так же смысл безразмерного времени от начала процесса коагуляции, выраженного периодах полураспада коллоида. Его отсчет, однако, начинается не с 0 , а с 1.

Теория Смолуховского и соответствующие уравнения не предусматривают какого-либо окончания процесса коагуляции, хотя он, безусловно, должен чем-то завершиться. В теории отсутствует возможность нахождения основной геометрической характеристики флокул – их размера, что делает недоступным расчет любых свойств, зависящих от размера частиц (флокул). Уравнения кинетики коагуляции могут приобрести практическое значение после нахождения связи между средним числом частиц в одной флокуле и их размером. Такую возможность предоставляют фрактальные свойства флокул. Эти свойства вытекают из того факта, что закон коагуляции флокул остается неизменным при их укрупнении. Отсюда следует, что структура крупных флокул подобна структуре мелких флокул, т.е. последние строят крупную флокулу по тем же «чертежам», по которым они сами были построены из еще более мелких флокул, включая самые мелкие флокулы, образованные из индивидуальных частиц.

Фундаментальное свойство фрактальных объектов заключается в наличии однозначной связи между характерным размером объекта и числом элементарных структурных элементов в его составе. Для флокул это соотношение между размером l (диаметром) флокулы и числом  первичных частиц в ней: =(l/r)^ф . В качестве параметров выступает диаметр частиц r и фрактальная размерность ф. Последняя характеризует плотность заполнения внутреннего пространства флокулы частицами дисперсной фазы. В трехмерном пространстве фрактальная размерность может принимать значения от 1 до 3, в том числе, дробные. Единица соответствует наиболее рыхлым флокулам, а тройка – максимально плотной упаковке частиц внутри флокулы. Таким образом, размер флокул становится доступным вычислению в любой момент времени от начала коагуляции, а с ним и зависящие от размера флокул свойства.

Среди свойств, зависящих от размера флокул, т.е. от времени, прошедшего от начала процесса коагуляции, важнейшим является доля объема, занимаемого во взвеси флокулами. Она может во много раз превышать долю дисперсной фазы, так как внутреннее пространство флокулы частично заполнено дисперсионной средой. Ее доля во внутрифлокулярном пространстве непрерывно растет по мере укрупнения флокул. Отсюда следует первый механизм прерывания процесса коагуляции – исчезновение свободной дисперсионной среды или, иначе говоря, увеличение доли объема, занятого флокулами до единицы. Фактически это означает переход системы в структурированное состояние, при котором взаимное положение частиц фиксировано и они теряют возможность двигаться и участвовать в коагуляционном процессе. В таком состоянии флокулы характеризуются некоторым критическим размером (числом частиц _c в одной флокуле), которое легко вычисляется из условия равенства единице объемной доли флокул во взвеси.

Другое важное свойство, которое изменяется в процессе коагуляции это скорость оседания частиц (флокул). Она прогрессивно растет с увеличением размера флокул, что ускоряет накопление осадка на дне сосуда и вызывает появление в верхней его части слоя жидкости, очищенной от частиц дисперсной фазы. Этот процесс так же имеет естественное ограничение. Очевидно, что процесс коагуляции прекратится, когда суммарная высота слоя осадка и слоя очищенной от частиц жидкости станет равной общей первоначальной высоте столба взвеси. Фактически это означает полное расслоение системы на две фазы –осадок и дисперсионную среду, т.е. исчезновение взвешенной части дисперсной фазы. Соответствующее критическое значение размера флокул (число частиц _s в одной флокуле) так же легко вычисляется из упомянутого условия при наличии зависимости высоты осадка и слоя жидкости от числа частиц во флокуле.

Существует еще один механизм прерывания процесса коагуляции. Он связан с конечной величиной силы сцепления частиц во флокуле и, следовательно, с ограниченной прочностью флокул. При достаточно большом размере флокулы разрушаются под действием собственного веса, так что их размер ограничен гравитационно равновесны размером флокул _g=F_c/mg , равным отношению силы сцепления частиц F_c (глубине минимума силовой кривой взаимодействия с обратным знаком) к силе веса частицы mg.

Задача заключается в определении процесса, лимитирующего коагуляцию – структурирование, расслоение или достижение гравитационно равновесного размера флокул, расчет параметров состояния системы (объемная доля флокул во взвеси, высота осадка и его плотность, высота слоя жидкости в верхней части сосуда) в любой момент времени от начала процесса коагуляции до его завершения и получение данных о распределении дисперсной фазы по высоте по окончании процесса.

Обозначения, наименования, размерности величин и формулы для их вычисления

m – масса частицы с поправкой на силу Архимеда, кг ……………m=v

u - скорость оседания частицы в поле сил тяжести, м/с …………u=2ga²/9_o

D - коэффициент диффузии, м²/с …………………………………..D=kT/в

n₁ - концентрация первичных частиц, 1/м

t - время от начала процесса коагуляции и оседания частиц, с

t* - время половинной коагуляции, с ……………………………….t* = 3₀/8kTn₁

n - общая концентрация флокул коагулята (1/м³) всех размеров в произвольный

момент времени t ………………………………………………..n = n₁/(1+ t/t*)

 = n₁/n- среднее число частиц в одной флокуле в момент времени t от начала процесса коагуляции ………………………………………………….. = 1+ t/t*

r - расстояние между центрами соседних связанных частиц, м

L - размер флокулы (диаметр описанной вокруг нее сферы), м

Основное соотношение фрактальной геометрии флокул, определяющее смысл

понятия "фрактальная размерность флокул" : ………………. = (L/r)^ф

ф - фрактальная размерность флокул коагулята

_f - доля объема занятая во взвеси флокулами коагулята ………_f =  ^(3-ф)/ф

(3-ф)/ф - показатель структурирования

Условие завершения процесса коагуляции путем перехода взвеси в структурированное состояние _f = 1 или _c= (1/)^ф/(3-ф)

_c - размер флокул (число частиц в одной флокуле) в момент перехода дисперсной системы в структурированное состояние.

H_s - высота слоя осадка в произвольный момент времени t от начала коагуляции, м H_s= ut*[ф/(ф+2)][^(ф+2)/ф -1] *

(ф+2)/ф - показатель расслоения.

_s - доля дисперсной фазы в верхнем слое осадка (на высоте H_s) в тот же момент времени t _s=  ^(ф-3)/ф

Эти две формулы (для H_s и для _s) задают в параметрической форме зависимость концентрации дисперсной фазы _s внутри осадка от высоты h, равной H_s в соответствующий момент времени. При структурировании концентрация дисперсной фазы не меняется и остается равной исходной концентрации по всей высоте структурированной части дисперсной системы.

H_L - толщина слоя очищенной от частиц дисперсионной среды в верхней части сосуда, м.

H_=H_s+H_L - суммарная высота слоя осадка и чистой среды, м

H_=ut*[ф/(2ф -1)][ ^{(2ф -1)/ф} - 1]

Высота H_L слоя дисперсионной среды в верхней части сосуда, освобожденной от частиц, вычисляется как разница H_ и H_s : H_L = H_ - H_s **

Условие завершения процесса коагуляции путем расслоения взвеси на осадок и слой дисперсионной среды над ним: H_= H или _s = {[(2ф-1)/ф](H/ut*)+1}^{ф/(2ф -1)}

_s -размер флокул в момент полного расслоения взвеси.

Фактический способ окончания коагуляции определится тем процессом, из двух указанных выше, который завершится раньше:

Если _c< _s , то коагуляция завершится структурированием дисперсной системы

Если _c> _s , то коагуляция завершится расслоением дисперсной системы.

В любом случае к моменту завершения процесса коагуляции на дне сосуда образуется осадок, а в его верней части появляется слой освобожденной от частиц дисперсионной среды. Высота того и другого вычисляется по формулам * и ** при замене в них произвольной величины  на _c при структурировании и на _s при расслоении. При структурировании высота слоя осадка и слоя жидкости может быть исчезающе малой. Тогда как при расслоении в сумме они равны первоначальной высоте столба взвеси.

Чем крупнее флокулы, размер которых растет по мере течения процесса коагуляции, тем меньше их прочность, поэтому коагуляция может так же прекратиться из-за разрушения больших рыхлых флокул на более мелкие флокулы под действием силы их собственного веса. В итоге установится гравитационно равновесный размера флокул _g. В случае достаточно крупных частиц разрушение идет до единичных частиц (_g=1), т.е. в процессе оседания коагуляция становится невозможной, но она будет иметь место в осадке.

_g - гравитационно равновесный размер флокул во взвеси ………………. _g=F_c/F_g

F_c - сила сцепления двух частиц во флокуле, Н (cм. тему “Экстремумы ...”) F_c= -F_min

Задание: Определить лимитирующий этап процесса коагуляции дисперсной системы, вычислить параметры ее конечного состояния, представить его графиком распределения дисперсной фазы по высоте.

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

1 Объемная доля дисперсной фазы 0,124

11 Высота сосуда м 0,228

5 Плотность дисп. фазы кг/м3 3140

6 Плотность среды кг/м3 929

7 Вязкость среды Па.с 0,001175

9 Размер частиц м 2,07E-06

10 Фрактальность флокул коагулята 1,814252

Приведенная сила сцепления Н/м 6,91E-06

Константа притяжения Дж 3,14E-21

Толщина защитной оболочки м 1,00E-08

Константы:

Константа Больцмана Дж/К 1,38.10-23

Температура К 293

Ускорение свободного падения м/с² 9,81

Расчет параметров кинетики коагуляции: Лимитирующий процесс: структурирование

Объем частицы м3 3,72E-17

Масса частицы кг 8,22E-14

Вес частицы Н 8,07E-13

Сила сцепления частиц Н 4,50E-11

Концентрация частиц 1/м³ 3,32E+15

Время половинной коагуляции с 32,77184

Скорость оседания одной частицы м/с 1,76E-05

Показатель структурирования (3-ф)/ф 0,65

Показатель осадка (ф+2)/ф 2,10

Показатель суммарного расслоения 1,45

Гравитационно равновесный размер флокул частиц 55,74145

Размер флокул при структурировании частиц 24,49856

Размер флокул при расслоении частиц 80,14413

Минимальный размер из перечисленных выше частиц 24,49856

Время оседания индивидуальной частицы с 12944,26

Таблица 6.1 - Кинетика коагуляции дисперсной системы

	t, с	f	s	Hs, м	H, м	HL, м	hL, м
1	0	0,12	1	0	0	0	0,227
3,35	77	0,27	0,45	0,0004	0,002	0,0015	0,226
5,70	154	0,38	0,32	0,0012	0,004	0,003	0,224
8,05	231	0,48	0,25	0,002	0,008	0,005	0,222
10,4	308	0,57	0,22	0,004	0,011	0,007	0,221
12,7	385	0,65	0,19	0,007	0,015	0,0087	0,219
15,1	462	0,73	0,17	0,010	0,020	0,010	0,218
17,4	539	0,80	0,15	0,014	0,025	0,010	0,217
19,8	616	0,87	0,14	0,018	0,030	0,011	0,216
22,1	693	0,93	0,13	0,023	0,035	0,012	0,215
24,5	770	1	0,12	0,028	0,040	0,012	0,215
			0,12	0,215
			0	0,215

Примечание: Жирным курсивом выделены служебные величины, предназначенные для использования программой.

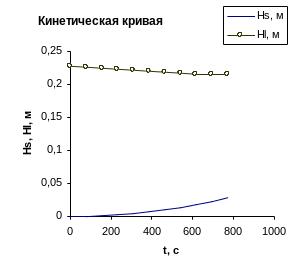
Рисунок 6.1 - Кинетика оседания суспензии в процессе коагуляции

Рисунок 6.2 - Распределение дисперсной фазы по высоте

после завершения процесса коагуляции.

7 РЕОЛОГИЯ ДИСПЕРСНЫХ СИСТЕМ

Реология изучает деформационные свойства материалов. Они описываются зависимостью деформации  от напряжения  или скорости деформации ’от напряжения. Простейшим видом деформации является деформация сдвига. По характеру зависимости деформации от напряжения материалы принято делить на твердые и жидкие материалы. Поведение твердых материалов под нагрузкой подчиняется закону Гука:  = G

Поведение жидкостей под действием сдвиговых напряжений подчиняется закону внутреннего трения Ньютона:  = ’

Течение жидкости это процесс увеличения ее деформации во времени

Деление материалов на твердые и жидкие условно, поскольку проявление тех или иных свойств зависит от режима деформирования. Широко распространены материалы, которые при малых напряжениях ведут себя как упругие, а при достаточно больших - как жидкие - текут под действием механических напряжений. Такие материалы называются пластическими. Они наиболее важны для технологии так как позволяют превращать материалы в изделия, поскольку пластическая деформация не сопровождается разрушением материала. Основной характеристикой пластичного материала является величина напряжения _s, при которой он приобретает способность течь, и называется предельным напряжением сдвига или пределом текучести или сдвиговой прочностью. Простейший в математическом смысле реологический закон, описывающий поведение пластичного материала, это закон Шведова-Бингама:

 = _s + * ’

Величина * , входящая в этот закон, называется пластической вязкостью.

Пластичность дисперсных систем обусловлена образованием коагуляционной структуры (см. тему 6). Фундаментальным свойством коагуляционных структур, а с ним и пластичных тел, является тиксотропность – способность структуры к обратимым изотермическим разрушениям и восстановлениям связей между частицами. Это и обеспечивает возможность течения материала без его разрушения, поскольку разрывы, возникающие в структурной сетке при течении, полностью восстанавливаются после прекращения течения и она полностью сохраняет свою прочность.

Реальные пластичные материалы имеют более сложную зависимость скорости сдвига от напряжения, чем это предусматривает закон Шведова-Бингама. Причина в том, что структурная сетка неоднородна по прочности фрагментов, из которых она образуется. Фрактальная модель коагуляционной структуры дает весь спектр прочностей ее фрагментов, что позволяет установить закон течения реальных пластичных материалов с коагуляционной структурой. Отличительная особенность их течения в том, что вместо постоянных реологических констант – вязкости или пластической вязкости*, поведение материала при деформировании описывается функцией =f(), определяющей величину вязкости в зависимости от величины действующего в материале напряжения. Жидкости, вязкость которых зависит от напряжения принято не вполне удачно принято называть неньютоновыми.

Вязкость  является универсальной характеристикой любых текучих материалов. Ее смысл и численное значение однозначно определяется законом внутреннего трения Ньютона: =/’ не зависимо от того является ли данный материал обычной (ньютоновой) жидкостью, линейно-пластичной (бингамовой) жидкостью или какой-либо иной. Задача данного упражнения заключается в нахождении реологического закона течения тиксотропной дисперсной системы, его представление в виде формулы для вязкости с конкретными значениями показателей степени, и иллюстрация в форме таблицы и в форме графиков зависимости скорости деформации и вязкости от напряжения – реологических кривых течения и вязкости соответственно.

Обозначения, наименования, размерности величин и формулы для их вычисления*

 - коэффициент формулы Эйнштейна, =2,5 для сферических частиц

 - вязкость взвеси невзаимодействующих между собой частиц, Па.с

формула Эйнштейна …………………………………………….=₀(1+)

модифицированное уравнение (Эйнштейна) для концентрированных взвесей

=₀/(1- )^

_m - прочность плотнейшей структуры при заданной силе сцепления двух частиц F_c, Н/м²

_m=3F_c/r²

 - показатель реологического уравнения ………………………..=2/(3-ф)

_s - прочность фрактальной структуры при заданной концентрации дисперсной фазы, Н/м²

_s=_m^

 - напряжение сдвига (независимая переменная в уравнениях реологии), Н/м²

_e - тиксотропно равновесная доля флокул в потоке

_e=1, =<_s

_e=(_s/)^1/, _s<<_m

_e=, >=_m

зависимость вязкости от напряжения ……………….=₀/(1-_e)^

 ’ - скорость сдвига, 1/с ……………………………………’=/

(Закон внутреннего трения Ньютона)

* Смотри так же обозначения на по теме Кинетика коагуляции

Задание: Найти зависимость вязкости и скорости сдвига от напряжения, представить ее таблично и графически (построить реологические кривые)

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

1 Объемная доля дисперсной фазы 0,124

9 Размер частиц м 2,07.10^-6

10 Фрактальность флокул коагулята 1,81

7 Вязкость среды Па.с 0,0012

Приведенная сила сцепления частиц Н/м 6,91.10^-6

Константы

Коэффициент формулы Эйнштейна 2,5

Расчет параметров реологического уравнения

Напряжение полного разрушения флокул Па 2,62

Показатель реологического уравнения 1,69

Предельное напряжение сдвига Па 0,077

Таблица 7.1 - Расчет реологических кривых

_s=0,077 Па , ₀=0,0012 Па.с

, Па	e	, Па.с	’, с-1
0			0
0,077	1		0
0,224	0,532	0,0078	28,5
0,370	0,395	0,0041	89,9
0,517	0,324	0,0031	165,4
0,663	0,279	0,0027	249,1
0,810	0,248	0,0024	338,0
0,956	0,225	0,0022	430,8
1,103	0,207	0,0021	526,6
1,249	0,192	0,0020	624,6
1,396	0,180	0,0019	724,5
1,543	0,169	0,0019	826,0
1,689	0,160	0,0018	928,8
1,836	0,153	0,0018	1032,7
1,982	0,146	0,0017	1137,7

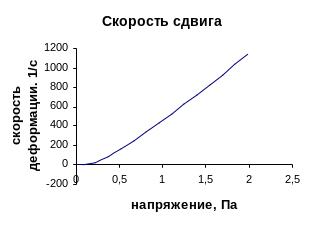
Рисунок 7.1 – Реологическая кривая течения

Рисунок 7.2 – Реологическая кривая вязкости

8 ПРЕДЕЛЬНО КОНЦЕНТРИРОВАННЫЕ СУСПЕНЗИИ (ПКС)

Важнейшая задача технологии дисперсных систем – обеспечение однородности распределения дисперсной фазы по всему объему системы. Существует несколько способов решения этой проблемы. В системах с коллоидным уровнем дисперсности (размером частиц порядка 10^-8 м и менее) достаточно эффективным может быть придание системе максимальной агрегативной устойчивости. В таком случае взвесь частиц может иметь достаточно большое время расслоения или приемлемую для практических целей величину перепада концентраций по высоте и отсутствие осадка в равновесном состоянии системы (см. тему 5). Для систем суспензионного типа (размер частиц 10^-7 – 10^-5 м) этот путь неприемлем, так как и без коагуляции происходит быстрое расслоение суспензии, причем осадок тем плотнее, чем больше агрегативная устойчивость суспензии.

Самый распространенный способ обеспечения однородности суспензионных составов это их структурирование (см. тему 6). В тех случаях, когда допустимо присутствие в системе различных вспомогательных компонентов, структурирование может быть вызвано их введением в суспензию. Они выполняют при этом роль загустителя (структурообразующего компонента). В качестве такового широко применяются органические полимеры (карбоксиметилцеллюлоза, нитроцеллюлоза, поливиниловый спирт и др.), крахмал, или высокодисперсные неорганические минералы и синтетические материалы (глина, каолин, аэросил, сажа). Прочность структурной сетки высокодисперсного компонента суспензии (см. тему 7) может быть достаточной для того, чтобы она могла выполнять функции несущей среды для крупных фракций суспензии. Этот принцип используется при подборе рецептуры красок, строительных растворов на основе цемента, растворов для бурения скважин и других.

В современной технологии широко используется получение прочных монолитных или умеренно пористых керамических материалов из высокодисперсных компонентов (огнеупорные элементы печей, радиокерамика и др.). Исходным продуктом для их производства служат предельно концентрированные суспензии. Содержание жидкой фазы в таких составах является важнейшим технологическим параметром суспензии. Чем оно меньше, тем меньше усадка отформованного из суспензии изделия при его сушке и обжиге, тем точнее выдерживается форма изделия и меньше внутренние напряжения, уровень которых определяет надежность и долговечность изделий. В то же время такие предельно концентрированные составы (ПКС) должны поддаваться формованию, т.е. сохранять способность течь. Этому благоприятствует минимизация сил сцепления частиц, т.е. придание суспензии максимальной агрегативной устойчивости.

По структурному типу ПКС относя к периодическим коллоидным структурам, что означает фиксацию частиц в узлах правильной (периодической), кристаллоподобной решетки. Количественное описание состояния и свойств таких суспензий подразумевает монодисперсность частиц. Только в этом случае структурную решетку можно характеризовать определенной величиной ее периода, который элементарно выражается через численную концентрацию частиц в суспензии.

Определения и формулы*

Существует предел n_m, до которого можно повышать концентрацию частиц n в дисперсной системе. Он наступает, когда объем 1/n приходящийся во взвеси на одну частицу уменьшается до объема самой частицы v , т.е n_m = 1/ v

Это значит, что во взвеси практически не остается свободной дисперсионной среды и дисперсная система состоит только из плотно упакованных частиц. Если частицы одинаковы по размеру и форме, то они при этом располагаются в узлах правильной решетки, образуя кристаллоподобную (периодическую) структуру. При плотнейшей упаковке одинаковые сферические частицы занимают 75% всего объема, а остальные 25% приходятся на межчастичные полости. По этой причине n_m = _m / v

где _m =0,75 при гексагональной упаковке и _m =0,53 при кубической упаковке частиц.

При наличии защитных оболочек эффективный объем V_е, занимаемый во взвеси одной частицей, больше чем ее собственный объем V см. задачи 1 и 5) и потому в приведенных выше формулах следует заменить V на V_е. Подробнее эти вопросы рассмотрены в зыдачах 1 и 5. Однако и после этого формула не будет отражать реальные условия стесненности частиц во взвеси вследствие нежесткости защитных оболочек. В частности, ионные оболочки (двойные электрические слои) формально имеют бесконечно толстые оболочки и, следовательно, при любой концентрации частиц они находятся в стесненных условиях (упираются друг в друга оболочками). Более адекватное описание состояния взвеси с точки зрения стесненности частиц дают потенциальные кривые взаимодействия трех частиц. В условиях стесненности на любую частицу вдоль любого направления действуют сразу две соседние частицы, что и отражается упомянутой трехчастичной функцией взаимодействия:

U=B(e^-æh1 + e^{- æh2}) - A(1/h₁ + 1/h₂) , где h₂=2h - h₁

h - рецептурное расстояние между поверхностями соседних частиц взвеси, которое определяется концентрацией частиц n: h = r - 2a, где r = (1/n)^1/3 рецептурное расстояние между центрами частиц, м.

Величины h₁ и h₂ представляют собой виртуальные расстояния центральной частицы от двух соседних частиц. Одна из них, например h₁, используется как независимая переменная для построения потенциальной кривой - графика зависимости энергии центральной частицы от ее положения относительно обеих соседних частиц. Он может иметь до трех максимумов и двух минимумов. Собственно стесненному состоянию соответствует кривая с одним минимумом в середине кривой (не обязательно в положительной области энергий) и двумя максимумами по бокам. Сильно размытый минимум с энергией близкой к нулю означает отсутствие стесненности. Если в середине так же находится максимум, а перед боковыми максимумами есть минимумы то будет возникать коагуляционная структура. Единственный максимум в середине ведет к стесненной коагуляции.

Конфигурация трехчастичной потенциальной кривой определяется концентрацией и размером частиц и концентрацией электролита. Ориентиром при подборе концентрации электролита с является его критическая концентрация с_к, поэтому ниже в задаче она задана относительной величиной с/с_к.

Задание: Определить структурное состояние суспензии и минимально необходимые изменения ее рецептуры (концентрации дисперсной фазы или концентрации электролита или размера частиц) для перехода в кристаллоподобное состояние.

Пример

Дано: вещество Ca₃(PO₄)₂

№ параметра

9 Размер частиц м 2,07^.10^-6

1 Концентрация дисп. фазы 0,124 (0,360)

Константа отталкивания дисп.фазы Дж 2,70^.10^-12

Константа притяжения дисп.фазы Дж 3,14^.10^-21

Относительная концентрация электролита доля от С_к 0,1

Расчет параметров взаимодействия частиц

Критическая величина параметра Дебая 3,16.10⁸

Объем частицы 3,72.10^-17

Число частиц 9,68.10¹⁵

Рецептурн. расстояние между центрами частиц 4,69.10^-6

Рецептурн. расстояние между частицами 5,51.10^-7

Глубина ямы Дж 6,49.10^-18

Энергия в точке симметрии U(h/2),Дж -1,43.10^-19

Заключение о состоянии взвеси периодическ. стр

Причина отсутствия кристаллоподобности

Таблица 8.1 - Расчет взаимодействия частицы с двумя соседними

шаг æh	æ, м-1	h, м	æh	строк	log U	Umax, Дж	Umin, Дж
0,867	3,16.107	5,51.10-7	17,4	20	-19	6,3510-18	-1,4310-19
æhi	h1, м	h2, м	U1, Дж	U2, Дж	U, Дж	h, нм	U, 10-19 Дж
0,0	1,21.10-9	5,50.10-7	7,47.10-23	-3,72.10-20	-3,71.10-20	1,21	-0,37
0,9	2,86.10-8	5,22.10-7	6,39.10-18	-3,91.10-20	6,35.10-18	28,6	63,47
1,8	5,60.10-8	4,95.10-7	2,62.10-18	-4,13.10-20	2,58.10-18	56,0	25,78
2,6	8,35.10-8	4,67.10-7	1,01.10-18	-4,37.10-20	9,66.10-19	83,5	9,66
3,5	1,11.10-7	4,40.10-7	3,43.10-19	-4,64.10-20	2,97.10-19	111	2,96
4,4	1,38.10-7	4,13.10-7	7,39.10-20	-4,95.10-20	2,45.10-20	138	0,24
5,2	1,66.10-7	3,85.10-7	-3,0.10-20	-5,30.10-20	-8,30.10-20	166	-0,83
6,1	1,93.10-7	3,58.10-7	-6,7.10-20	-5,69.10-20	-1,23.10-19	193	-1,23
7,0	2,21.10-7	3,30.10-7	-7,6.10-20	-6,13.10-20	-1,37.10-19	221	-1,37
7,8	2,48.10-7	3,03.10-7	-7,5.10-20	-6,62.10-20	-1,42.10-19	248	-1,41
8,7	2,75.10-7	2,75.10-7	-7,1.10-20	-7,13.10-20	-1,43.10-19	275	-1,42
9,6	3,03.10-7	2,48.10-7	-6,6.10-20	-7,54.10-20	-1,42.10-19	303	-1,41
10,4	3,30.10-7	2,21.10-7	-6,1.10-20	-7,61.10-20	-1,37.10-19	330	-1,37
11,3	3,58.10-7	1,93.10-7	-5,7.10-20	-6,66.10-20	-1,23.10-19	358	-1,23
12,2	3,85.10-7	1,66.10-7	-5,3.10-20	-3,01.10-20	-8,30.10-20	385	-0,83
13,0	4,13.10-7	1,38.10-7	-4,9.10-20	7,39.10-20	2,45.10-20	413	0,24
13,9	4,40.10-7	1,11.10-7	-4,6.10-20	3,43.10-19	2,97.10-19	440	2,96
14,8	4,67.10-7	8,35.10-8	-4,4.10-20	1,01.10-18	9,66.10-19	467	9,66
15,6	4,95.10-7	5,60.10-8	-4,1.10-20	2,62.10-18	2,58.10-18	495	25,78
16,5	5,22.10-7	2,86.10-8	-3,9.10-20	6,39.10-18	6,35.10-18	522	63,47
17,4	5,50.10-7	1,21.10-9	-3,7.10-20	7,47.10-23	-3,71.10-20	550	-0,37
8,7	2,75.10-7	2,75.10-7	-7,1.10-20	-7,13.10-20	-1,43.10-19	275	########

Примечание: в первых двух строках таблицы приведены параметры, используемые при электронном заполнении таблицы.

Рисунок 8.1 - Потенциальная кривая взаимодействия частицы с двумя ближайшими соседями в стесненных условиях.

Л И Т Е Р А Т У Р А

1. Д.А. Фридрихсберг. Курс коллоидной химии. - Л.: Химия, 1984. - 368 с.

2. Расчеты и задачи по коллоидной химии. Под ред. В.И. Барановой. М.: 1989. Высш. школа. 288 с.

3. Е.Е. Бибик, Е.А. Попова. Фрактальная модель коагулирующей суспензии. ЖПХ. 2000. Т. 73. Вып. 1. С. 19-23.

4. Е.Е. Бибик. Реология дисперсных ситем. - Л.: Изд-во Ленингр. ун-та, 1981. - 182 с.

5. Д.С. Фирсов, С.В. Фирсов. Microsoft Excel на работе и дома. - М.: ООО "Аквариум-Принт", ОАО "Дом печати-Вятка". 2004.- 192 с.

С О Д Е Р Ж А Н И Е

Введение ......................................................................................................... 3

1. Рецептурные и геометрические характеристики дисперсных систем 5

2. Двойной электрический слой .................................................................. 6

3. Потенциальные кривые взаимодействия частиц .................................. 9

4. Экстремумы функций взаимодйствия .................................................... 11

5. Молекулярно-кинетические свойства дисперсных систем .............. 14

6. Кинетика коагуляции и фрактальные свойства ..................................... 18

7. Реология дисперсных систем ................................................................. 23

8. Предельно концентрированные суспензии ................................... 26

Литература ........................................................................................................ 30

Кафедра коллоидной химии

Учебное пособие