- •1. Определители 2-го и 3-го порядков. Основные свойства.
- •2. Минор и алгебраическое дополнение. Понятие определителя n-го порядка и его вычисление.
- •3. Матрицы, действия над ними. Обратная матрица.
- •4. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.
- •5. Правило Крамера.
- •6. Решение систем линейных алгебраических уравнений матричным методом.
- •7. Векторы. Линейные операции над векторами и их свойства. Проекция вектора на ось.
- •8. Линейная зависимость векторов. Разложение вектора по базису.
- •9. Декартова система координат. Координаты вектора. Направляющие косинусы, длина вектора. Деление отрезка в данном соотношении.
- •10. Скалярное произведение векторов, его свойства, вычисление и применение.
- •11. Векторное произведение векторов, его свойства, вычисление и применение.
- •12. Смешанное произведение векторов, его свойства, вычисление и применение.
- •13. Прямая линия на плоскости. Различные способы задания. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой на плоскости.
- •14. Плоскость в пространстве. Различные способы задания. Взаимное расположение плоскостей. Расстояние от точки до плоскости.
- •15. Прямая в пространстве. Взаимное расположение прямых в пространстве.
- •16. Взаимное расположение прямой и плоскости в пространстве.
- •17. Полярная система координат.
- •18. Кривые 2-го порядка: эллипс, гипербола, парабола. Определение и канонические уравнения. Исследование формы кривых по их каноническим уравнениям.
- •19. Поверхности 2-го порядка. Цилиндрические поверхности и поверхности вращения. Исследование поверхностей методом сечений.
- •20. Функция, область ее определения и способы задания. Сложные и обратные функции.
- •21. Числовые последовательности. Предел числовой последовательности. Число е. Натуральные логарифмы.
- •22. Предел функции в точке, односторонние пределы.
- •23. Предел функции в бесконечности. Геометрическая иллюстрация.
- •24. Бесконечно малые функции и их свойства.
- •25. Бесконечно большие функции. Связь между бесконечно малыми и бесконечно большими.
- •26. Основные теоремы о пределах.
- •27. Первый и второй замечательный пределы.
- •28. Сравнение бесконечно малых функций.
- •29. Непрерывность функций в точке и на отрезке. Точки разрыва функций и их классификация.
- •30. Свойства функций, непрерывных в точке.
- •31. Свойства функций, непрерывных на отрезке и их геометрический смысл.
- •32. Задачи, приводящие к определению производной. Производная функции, ее геометрический и механический смыслы. Односторонние производные. Производная сложной и обратной функции.
- •33. Дифференциал функции и его геометрический смысл. Свойства дифференциала и инвариантность его формы. Применение дифференциала к приближенным вычислениям.
- •38. Правило Лопиталя.
- •39. Применение дифференциального исчисления к исследованию функций и построению их графиков.
- •40. Функции нескольких переменных. Область определения. Предел и непрерывность функций 2-х переменных. Частные приращения и частные производные.
- •41. Полный дифференциал функции нескольких переменных. Применение дифференциала функции 2-х переменных к приближенным вычислениям. Частные производные высших порядков.
- •42. Экстремум функции нескольких переменных. Необходимые и достаточные условия экстремума функции 2-х переменных. Исследование функции 2-х переменных на экстремум.
- •47. Основные методы интегрирования: непосредственное, замена переменной, по частям.
- •48. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его основные свойства.
- •53. Приложения определенных интегралов к решению задач геометрии и физики.
- •54. Основные понятия теории обыкновенных дифференциальных уравнений. Ду 1-го порядка. Формулировка теоремы существования и единственности решения задачи Коши.
- •56. Однородные ду 1-го порядка.
- •57. Линейные ду 1-го порядка.
- •59. Линейные однородные ду 2-го порядка, свойства их решений.
- •60. Линейные однородные ду 2-го порядка с постоянными коэффициентами.
- •61. Линейные неоднородные ду 2-го порядка. Теорема о структуре их общего решения.
- •62. Лнду 2-го порядку с постоянными коэффициентами и специальной правой частью.
10. Скалярное произведение векторов, его свойства, вычисление и применение.
Скалярным произведением называется
число = произведению длин этих векторов
на косинус угла между ними (a∙b
или (a; b)).
Имеем a∙b
= |a|*|b|*cosα.
Свойства: 1) a∙b
= b∙a. 2) a∙a
= a2 = |a|2.
3) Если a ┴
b, то a∙b
= 0. 4) Если a ≠ 0, b
≠ 0 и a∙b =
0, то a ┴ b.
5) Пусть λϵR, то λa∙b
= a∙λb =
λ(a∙b). 6)
(a+b)∙c
= a∙c + b∙c.
Если вектора имеют свои координаты, то
a∙b = x1x2
+ y1y2
+ z1z2.
Имеем
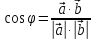 . Скалярное произведение используется
в математике, физике, для вычисления
работы А=F∙S
. Скалярное произведение используется
в математике, физике, для вычисления
работы А=F∙S
11. Векторное произведение векторов, его свойства, вычисление и применение.
Векторным произведением 2-х векторов а
и b называется вектор с
для которого: 1)
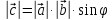 .
2) c перпендикулярно
плоскости в которой можно расположить
а и b – с ┴
b, c ┴
a. Свойства: 1) а х b
= -b х а. 2) а х b
= 0, когда a и b
коллинеарны или хотя бы 1 из векторов =
0. 3) λа х b = а х λb
= λ(а х b), где λϵR.
4) (a+b) x
c = a x
c + b x
c. Если 2 вектора заданы
своими координатами, то
.
2) c перпендикулярно
плоскости в которой можно расположить
а и b – с ┴
b, c ┴
a. Свойства: 1) а х b
= -b х а. 2) а х b
= 0, когда a и b
коллинеарны или хотя бы 1 из векторов =
0. 3) λа х b = а х λb
= λ(а х b), где λϵR.
4) (a+b) x
c = a x
c + b x
c. Если 2 вектора заданы
своими координатами, то
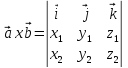 .
Используется в геометрии, можно так
находить площадь параллелограмма
.
Используется в геометрии, можно так
находить площадь параллелограмма
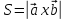 .
В физике можно использовать для вычисления
момента силы.
.
В физике можно использовать для вычисления
момента силы.
12. Смешанное произведение векторов, его свойства, вычисление и применение.
Смешанным произведение 3-х векторов
называется число, которое получается
при скалярном произведении векторов a
x b и c.
Свойства: 1)
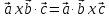 .
2) a x b∙c
= 0, когда векторы являются компланарными.
3) abc = cab =
bca = -bac = -acb
= -cba. Если векторы заданы
своими координатами, то
.
2) a x b∙c
= 0, когда векторы являются компланарными.
3) abc = cab =
bca = -bac = -acb
= -cba. Если векторы заданы
своими координатами, то
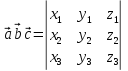 .
Используется в геометрии для расчета
объема:
.
Используется в геометрии для расчета
объема:
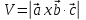
13. Прямая линия на плоскости. Различные способы задания. Взаимное расположение прямых на плоскости. Расстояние от точки до прямой на плоскости.
Вектор, перпендикулярный данной прямой
– нормальный. Уравнение прямой, проходящей
через данную точку перпедикулярной
заданному вектору –
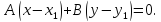 Уравнение прямой, лежащей в плоскости
Oxy (ОБЩЕЕ УРАВНЕНИЕ) – Ax
+ By + C = 0.
Уравнение прямой, проходящей через
точку (0;
Уравнение прямой, лежащей в плоскости
Oxy (ОБЩЕЕ УРАВНЕНИЕ) – Ax
+ By + C = 0.
Уравнение прямой, проходящей через
точку (0;
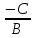 )
и перпендикулярно вектору n
(A; B) –
)
и перпендикулярно вектору n
(A; B) –
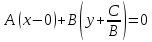 .
Если вектор || данной прямой – направляющий
вектор. Каноническое уравнение –
.
Если вектор || данной прямой – направляющий
вектор. Каноническое уравнение –
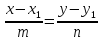 .
Уравнение прямой, проходящей через
данную точку в заданном направлении –
.
Уравнение прямой, проходящей через
данную точку в заданном направлении –
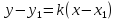 ,
где k = tgα.
Уравнение прямой с угловым коэффициентом
– y = kx + b
(если b=0, то прямая через
начало координат, если k=0,
то прямая || Ox). Уравнение
прямой, проходящей через 2 данные точки
–
,
где k = tgα.
Уравнение прямой с угловым коэффициентом
– y = kx + b
(если b=0, то прямая через
начало координат, если k=0,
то прямая || Ox). Уравнение
прямой, проходящей через 2 данные точки
–
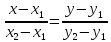 .
2 пересекающиеся прямые не ┴
друг другу –
.
2 пересекающиеся прямые не ┴
друг другу –
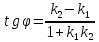 .
Если прямые || или совпадают, то α1
= α2 и k1 = k2.
Расстояние от точки до прямой –
.
Если прямые || или совпадают, то α1
= α2 и k1 = k2.
Расстояние от точки до прямой –
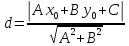
14. Плоскость в пространстве. Различные способы задания. Взаимное расположение плоскостей. Расстояние от точки до плоскости.
Уравнение плоскости, проходящей через
данную точку – A(x-x1)
+ B(y-y1)
+ C(z-z1)
= 0. Общее уравнение 1-ой степени с 3-мя
переменными – Ax + By
+ Cz + D = 0.
Уравнение плоскости в отрезках на осях
координат –
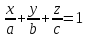 .
Уравнение плоскости, проходящей через
3 данные точки –
.
Уравнение плоскости, проходящей через
3 данные точки –
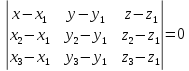 .
1 из смежных двугранных углов между
плоскостями –
.
1 из смежных двугранных углов между
плоскостями –
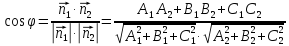 .
Свойства – 1) 2 плоскости перпендикулярны
тогда, когда их нормальные векторы
перпендикулярны, тогда A1A2
+ B1B2
+ C1C2
= 0. 2) 2 плоскости || тогда, когда их
нормальные векторы коллинеарны, т.е.
.
Свойства – 1) 2 плоскости перпендикулярны
тогда, когда их нормальные векторы
перпендикулярны, тогда A1A2
+ B1B2
+ C1C2
= 0. 2) 2 плоскости || тогда, когда их
нормальные векторы коллинеарны, т.е.
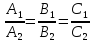 .
Расстояние от точки до плоскости –
.
Расстояние от точки до плоскости –