5. Правило Крамера.

Теорема (правило Крамера для системы nxn) – Если главный определитель ∆ системы линейных уравнений ≠ 0, то система совместна и имеет 1 решение, которое находится по формулам .

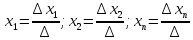6. Решение систем линейных алгебраических уравнений матричным методом.

Имеем 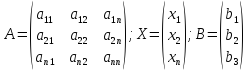. На основании правила умножения матриц заменим систему уравнений матричным уравнением с неизвестной матрицей Х: AX=B. Пусть А имеет обратную матрицу А^-1, умножив матричное уравнение на А^-1 слева, получим: А^-1∙А∙Х = А^-1∙В.

Т.к. А∙А^-1 = Е, а Е∙Х = Х, то имеем Х = В∙А^-1 – матричная запись решения системы линейных уравнений.

7. Векторы. Линейные операции над векторами и их свойства. Проекция вектора на ось.

Геометрическим вектором называется направленный отрезок АВ. Вектор ВА (или -АВ) – противоположный вектору АВ. Длиной вектора АВ или его модулем называется длина соответствующего отрезка АВ. Перемещение вектора в пространстве – параллельный перенос. 2 вектора называются равными, если параллельным переносом их можно совместить (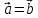). Если начало и конец вектора совпадают, то такой вектор называется нулевым (). 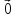Если 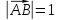, то вектор называется единичным. Векторы называются коллинеарными, если их можно совместить (нулевой вектор коллинеарен любому векторы). Векторы называются компланарными, если их можно разместить в одной плоскости. 1) Сложение 2-х векторов

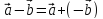
2) Умножение вектора на число

Углом между 2-мя векторами называется меньший из 2-х угол между ними (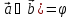. Если угол = 90^о, то векторы называются перпендикулярными (ОРТО). Имеем вектор АВ

Число х_В – х_А – проекция вектора на ось (может быть +, -, 0). Ох =.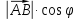

8. Линейная зависимость векторов. Разложение вектора по базису.

Векторы а₁, а₂, … , а_n называются линейно-зависимыми, если существуют такие числа с₁, с₂, … , с_n, не все = 0, для которых имеет место равенство с₁а₁ + с₂а₂ + … + с_na_n = 0. Векторы а₁, а₂, … , а_n линейно-независимы если равенство с₁а₁ + с₂а₂ + … + с_na_n = 0 выполняется только при условии с₁ = с₂ = … = с_n = 0. Базис на прямой – любой ненулевой вектор этой прямой, на плоскости – любые 2 неколлинеарных вектора этой плоскости, взятые в определенном порядке, в пространстве – любые 3 некомпланарных вектора, выбранные в определенном порядке (на плоскости и в пространстве сколько угодно базисов). Если вектор а – базис на прямой и b – вектор этой прямой, то b = λa (а и b линейно-зависимы). Если (a, b) – базис на плоскости и c – вектор этой плоскости, то c = αa + βb (a, b, c, линейно-зависимы). Если (a, b, c) – базис в пространстве и d – вектор в этом пространстве, то d = αa + βb + γc (a, b, c, d линейно зависимы). Все числа единственны (α, β, γ, λ). Число λ – координата вектора b на прямой в базисе а и т.д.

9. Декартова система координат. Координаты вектора. Направляющие косинусы, длина вектора. Деление отрезка в данном соотношении.

Пусть i, j, k единичные с общим началом 0 взаимно перпендикулярные 3 вектора пространства и пусть (i, j, k) – базис этого пространства (ортонормированный). Через эти вектора проведем Х, Y, Z соответственно базисным векторам (прямые – оси координат, точка О – начало). Совокупность точки О и осей – Декартовая система координат пространства. Также и с прямоугольной Декартовой системы на плоскости (базис (i, j), оси X, Y). Имеем систему координат в пространстве, тогда вектор АВ имеет координаты (х₂-х₁, у₂-у₁, z₂-z₁). Длина вектора |AB|=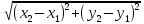.