1. Определители 2-го и 3-го порядков. Основные свойства.

Определителем 2-го порядка называется число, обозначаемое символом и вычисляемое по формуле 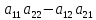. Матрица – таблица, а определитель – число. Определителем 3-го порядка называется число, обозначаемое символом и вычисляемое по формуле .

2. Минор и алгебраическое дополнение. Понятие определителя n-го порядка и его вычисление.

Определителем n-го порядка называется число, обозначаемое символом и вычисляемое по формуле 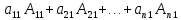, где A_ij (i=1,2,…,n) – определитель (n-1)-го порядка, полученный из исходного, вычеркиванием 1-го столбца и i-той строки и умножением полученного определителя на (-1)ⁱ⁺¹ .

Если в матрице вычеркнуть i-тую строку и j-ый столбец, а расположение остальных элементов оставить прежним, то получится квадратная матрица (n-1)-го порядка. Ее определитель обозначается M_ij и называется минором (M₃₃=). Алгебраическим дополнением матрицы называется число A_ij=(-1)^i+j∙M_ij. Теорема (о разложении определителя по столбцу (строке)) – Определитель матрицы А = сумме произведений всех элементов некоторого столбца (строки) на их алгебраическое дополнение.

3. Матрицы, действия над ними. Обратная матрица.

1) Сложение матриц (одинаковое кол-во строк и столбцов) – A(a_ij)_mxn + B(b_ij)_mxn= C(c_ij)_mxn, где С_ij = a_ij + b_ij. 2) Произведение матрицы на число – A(a_ij)_mxn * число α = αА = (α*a_ij)_mxn. 3) Произведение матриц (кол-во элементов в строках матрицы А = кол-ву элементов в столбцах матрицы В), А(а_ij)_mxn, B(b_ij)_nxl – соответственные. А(а_ij)_mxn * B(b_ij)_nxl = С(с_ij)_mxl, где c_ij = a_i1*b_1j + a_i2*b_2j +…+ a_in*b_nj (i=1,…,m; j=1,…,l). Элемент матрицы С, стоящей в i-той строке и j-том столбце = сумме произведений соответствующих элементов i-той строки матрицы А и j-того столбца матрицы В. Свойства умножения матриц – 1) Произведение матрицы может быть нуль матрицы, хотя оба сомножителя не являются нуль-матрицами 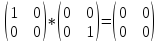. 2) Произведение матриц АВ ≠ ВА, но, если АВ=ВА, то матрицы А и В перестановочны (коммутируют). 3) Произведение матриц (АВ)*С=А*(ВС). 4) (А+В)*С=АС+ВС. 5) α(АВ)=А(αВ).

Если А (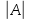) ≠ 0, то матрица называется невырожденной. Если А () = 0, то вырожденной (особой). Матрица А^-1 называется обратной по отношению к квадратной матрице А, если

АА^-1 = А^-1А = Е, где Е – единичная матрица. Теорема – Для существования обратной матрицы необходимо и достаточно, чтобы ее определитель был ≠ 0, то есть, чтобы матрица была невырожденной. (Док-во).

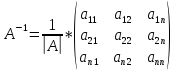
4. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.

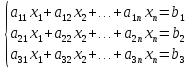Числа а_ij называются коэффициентами системы уравнений. Числа b₁, b₂, b_m называются свободными членами. Если b_i=0 и i=1,…,m, то система однородная. Х₁, х₂, х₃ – решения системы, если система обращается в тождество. Если имеет решение – совместная, наоборот – несовместная. Если только 1 решение – определенная, если >1 решений – неопределенная. Ранг матрицы – порядок самого старшего минора этой матрицы ≠ 0. Теорема – Для того, чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг ее матрицы А = рангу расширенной матрицы В. Если r(A)=r(B)= числу неизвестных, то система имеет только 1 решение. Если r(A)=r(B), но < числа неизвестных, то система имеет ∞ число решений.