7 Моменты инерции твердого тела. Момент инерции относительно полюса. Момент инерции относительно оси. Момент инерции тела относительно плоскости. Момент инерции

мОМЕНТОМ ИНЕРЦИИ I тела относительно точки, оси или плоскости называется сумма произведений массы точек тела m_i, на квадраты их расстояний r_i до точки, оси или плоскости:

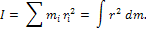
Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояний от этой точки до плоскости.

Момент инерции тела относительно оси является мерой инерции тела во вращательном движении вокруг этой оси.

Момент инерции тела может быть также выражен через массу М тела и его радиус инерции r:

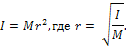
Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

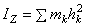
Центробежный момент инерции

        произведение инерции, одна из величин, характеризующих распределение масс в теле (механической системе). Ц. м. и. вычисляются как суммы произведений масс m_к точек тела (системы) на две из координат x_k, у_к, z_k этих точек:

         

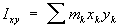
8 Теорема о моментах инерции относительно параллельных осей (теорема Штейнера). Осевые моменты инерции некоторых однородных простейших симметричных тел.

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_C относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

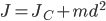
где:

J_C — известный момент инерции относительно оси, проходящей через центр масс тела;

J — искомый момент инерции относительно параллельной оси;

m — масса тела;

d — расстояние между указанными осями.

9 Теорема о движении центра масс механической системы. Следствия из теоремы.

Следствие 1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Так как ускорение центра масс равно нулю,   .

            Следствие 2.  Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.

получим окончательно:

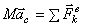                       (4)

Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.Сравнивая с уравнением дви­жения материальной точки, получаем другое вы­ражение теоремы: центр масс системы движется как мате­риальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Проектируя обе части равенства  на координатные оси, получим:

     

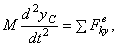
Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.

Значение доказанной теоремы состоит в следующем.

1) Теорема дает обоснование методам динамики точки. Из урав­нений видно, что решения, которые мы получаем, рассмат­ривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т.е. имеют вполне конкрет­ный смысл.