1 Основные определения динамики. Основные законы динамики(закон инерции, основной закон динамики, третьи закон ньютона, закон независимости действия сил)

Динамикой- называется раздел механики, в котором изучаются законы движения материальных тел под действием сил.

Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь

Законы динамики :

Первый закон (закон инерции), изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямо­линейного движения до тех пор, пока приложенные силы не за­ставят ее изменить это состояние. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета 

Второй закон (основной закон динамики)   произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы ma = F .

Третий закон (закон равенства действия и противодействия)  две ма­териальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны

Четвертый закон (закон независимого действия сил): При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия  других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.

2 Динамика точки. Дифференциальные уравнения движения материальной точки. Две основные задачи динамики.

Динамика – это раздел теоретической механики изучающий движения материальных точек и твёрдых тел под действием приложенных к ним. В динамике решают две задачи.

Основные задачи динамики : 1.(Прямой) Зная массу точки и зная закон ее движения определяют действующие на точку силы. 2. (Обратный) Зная массу точки и зная действующие на ее силы определяют закон ее движения.

Дифференциальное уравнение движения.

1)

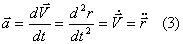
2)х=х(t)

Y=y(t)

Z=z(t)

3 Колебания материальной точки. Свободные колебания материальной точки на пружине. Свободные колебания математического маятника.

Колебания возникают при наличии так называемой восстанавливающей силы (это обязательное условие).

Общим признаком всех калебания являеться их многократное повторение через определенный промежуток времени.

Необходимым условием наличия колебат. Процесс явл. Восстанавливающие силы.

Кроме восстонав. Силы при колебании на точку может действовать так же возмущающая сила зависищая от времени.

Еще одна сила которая рассматриваеться при колебаниях явл. Сила сопротивления(силой вязкого трения).

Колебательный процесс класифицируеться:

1. Свободные колебания( присуствие только восстанавливающей силы)

2 ) Свободное колебание при вязком сопротивлении ( затухающие колебания)(присуствует восстанавл. И сила вязкого трения)

3 ) Вынужденное колебание ( присуств. Своостанавл. И возмущающая силы)

Свободные колебания ; обозначив c/m=k², с –жесткость пружины

Т=2π/k, периуд колебания

Математический маятник – колеблющаяся материальная точка, подвешенная

 на невесомой и нерастяжимой нити. К этой модели ближе всего массивное

тело (шар), размер (диаметр) которого много меньше длины нити.