4°. Признаки сходимости произвольных рядов

Здесь мы рассматриваем ряды, члены которых могут быть любыми вещественными или мнимыми числами. Начнем с частного, но весьма важного для приложений случая – с рядов, которые принято называть знакочередующимися.

Пусть {a_k} – последовательность положительных чисел. Рассмотрим. ряд . Ряды такой структуры и называют знакочередующимися.

Теорема 7. ( Признак Лейбница ) Пусть последовательность {a_k} строго убывает и стремится к нулю. Тогда ряд сходится; а его сумма S удовлетворяет неравенствам 0 < S ≤ a₁.

► Пусть n – некоторое четное число: n = 2l , l N. В сумме S_2l сгруппируем слагаемые :

S_2l = = (а₁ –a₂) + ( a₃ – a₄) + … +(a_2l-3 –a_2l-2 ) + (a_2l-1 –a_2l )

Так как {a_k} строго убывает,то разность в каждой из скобок положительна; значит, S_2l > 0 и S_2(l+1) > S_2l , т.е. последовательность {S_2l } - это строго возрастающая последовательность положительных чисел. Сгруппируем теперь слагаемые в сумме S_2l иначе :

S_2l = a₁ – ( a₂ –a₃ ) – ( a₄ –a₅ ) - … - ( a_2l-2 –a _2l-1 ) – a_2l .

Отсюда ясно, что S_2l < a₁. Таким образом, строго возрастающая последова- тельность { S_2l} ограничена сверху числом a₁; значит, она сходится. Обозна- чим ее предел через S. Из свойств { S_2l } следует: 0 < S ≤ a₁

Покажем, что S есть сумма ряда , т.е., что S = lim S_n , где S_n = = . Пусть n – некоторое нечетное число: n = 2l –1 , l N. Заметим : S_2l-1 = = S_2l - a_2l → S, так как S_2l → S, а a_2l → 0. Таким образом, обе подпосле- довательности {S_2l} частичных сумм с четными номерами и {S_2l-1} частичных сумм с нечетными номерами сходятся к S; значит, вся последовательность {S_n} имеет тот же предел

Итак, ряд сходится, а его сумма S удовлетворяет неравенствам 0< S ≤ a₁. ◄

Пример 10. Рассмотрим ряд , где λ – некоторое вещественное число. Это знакочередующийся ряд; здесь a_k = . Если λ ≤0 , последователь- ность {a_k}, очевидно, не стремится к нулю, и поэтому при таких λ ряд расхо- дится. При λ > 0 последовательность {a_k} строго убывает и стремится к ну- лю; значит, по признаку Лейбница ряд сходится.

В следующей теореме члены ряда - любые числа, быть может, мнимые. Из их модулей составим новый ряд ; члены этого ряда неотрицательны.

Теорема 8. Если сходится ряд , то сходится и ряд .

► Зададим некоторое ε > 0. Так как сходится, в силу критерия Коши (свойство 1, 2˚ ) существует натуральное n_ε такое, что при всех n > n_ε и любых натуральных р справедливо . Ho при этих n и p , т.е., для ряда выполнены требования критерия Коши:

N N N ( n > n_ε ) ,

поэтому ряд сходится . ◄

Пример 11. Рассмотрим ряд , где φ и λ – вещественные числа. Так как │exp(ikφ)│= 1, то . Отсюда ясно, что при λ ≤ 0 общий член рассматриваемого ряда не стремится к нулю, поэтому ряд расходится, а при λ > 1 ряд сходится ( см. пример 6), значит, сходится и рассматриваемый ряд. Его поведение при будет выяснено ниже с помощью признака Дирихле.

Лемма Абеля. Пусть и - наборы комплексных чисел Обозначим: V_q= ; V = max { |V₁| , |V₂| , … , |V_p| } . Тогда :

1. 

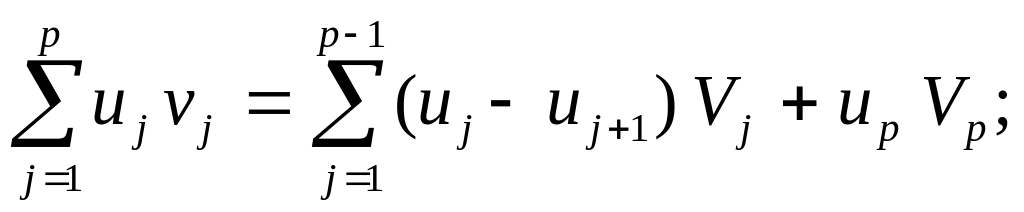
2. 2) если u₁ ≥ u₂ ≥ … ≥ u_p > 0 , то .

► Заметим : V₁ = v₁, а при j = 2,3, …, p v_j = V_j – V_j-1. Значит,

Раскрыв здесь скобки и приведя затем подобные, получим равенство 1).

◄

Теорема 9. ( Признак Дирихле ) Пусть - монотонная невозрастающая последовательность положительных чисел, а - последовательность комплексных чисел. Обозначим: В_р = . Если 1) и 2) существует М > 0 такое, что М при всех р N, то ряд сходится.

► Покажем, что ряд удовлетворяет требованиям критерия Коши N N N ( n > n_ε )

Зададим ε > 0. По условию 1) , значит, найдется натуральное n _ε такое, что из k > n _ε следует . Пусть n и р – натуральные числа, причем n > n _ε. Имеем: , где u _j = a_n+j , v _j = b _n+j . Заметим: u₁ ≥ u₂ ≥ … ≥ u_p > 0 . Обозначим: V_q = , V = max { |V₁| , |V₂| , … , |V_p| }. Так как V_q = = B_n+q – B_q, то при любом натуральном q имеем : | V_q | ≤ ≤ | B_n+q| + |B_q| ≤ 2M . Значит, V ≤ 2M . В силу утверждения 2) леммы Абеля , т.е. | | ≤ 2М a_n+1. Отсюда и из неравенствa следует : | | < ε . Таким образом, для произвольно заданного ε>0 существует натуральное n _ε , удовлетворяющее требованию критерия Коши ; поэтому ряд сходится. ◄

Пример 12. Вернемся к рассмотрению ряда . Пусть 0 < λ ≤ 1. Ввиду 2π – периодичности exp(ikφ), достаточно рассматривать . Если φ = 0, ряд превращается в , который при 0 < λ ≤ 1 расходится ( пример 6). Пусть φ . При всяком k N положим где q . Заметим: при 0 < λ ≤ 1 последовательность убывает и стремится к нулю; далее, при φ q отлично от единицы, поэтому B_p = , и, значит, |B_p| , где М от р не зависит. Таким образом, последовательности и удовлетворяют требованиям признака Дирихле, значит, ряд , т.е. при 0 < λ ≤ 1 и φ сходится.

Теорема 10. ( Признак Абеля) Пусть - невозрастающая последова- тельность положительных чисел, а - последовательность комплексных чисел. Если сходится ряд , то сходится и ряд .

► Обозначим: . Заметим: {c_k} – невозрастающая бесконечно малая последовательность положительных чисел; {B_p} – последовательность частичных сумм сходящегося ряда, значит, это сходя- щаяся и потому ограниченная последовательность. По признаку Дирихле ряд , т.е. сходится. Но , а это означает, что ряд является суммой двух сходящихся рядов и . Следовательно ( свойство 5, 2˚ ), ряд сходится. ◄