Тема 4.6Приложение кратных интегралов.
4.6.1 Приложение двойных интегралов.
4.6.2 Приложение тройных интегралов.
4.6.3 Приложение криволинейных интегралов.
4.6.1 Приложение двойных интегралов.
1) Вычисление площадей в декартовых координатах.
(4.6.1)
Типовой пример.
Вычислить площадь фигуры, ограниченной линиями y2 = 4x + 4; x + y – 2 = 0.
Решение.
Линии
пересекаются в двух точках: (0, 2) и (8, -6).
Таким образом, область интегрирования
ограничена по оси ОХ
графиками кривых от
до х = 2 – у,
а по оси ОУ
– от –6 до 2. Тогда искомая площадь равна:
S
=
2) Вычисление площадей в полярных координатах.
(4.6.2)
3) Вычисление объемов тел.
Объём Vцилиндроида, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z=0 и с боков прямой цилиндрической поверхностью, вырезывающей на плоскости ХОУ область S, равен:
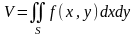(4.6.3)
Типовой пример.
Вычислить объём, ограниченный поверхностями: x2 + y2 = 1, x + y + z =3 и плоскостью ХОY.
Решение.
Пределы
интегрирования: по оси ОХ:
по оси ОY: x1 = -1; x2 = 1;
.
4)Вычисление моментов инерции плоских фигур.
Пусть площадь плоской фигуры (область S) ограничена линией, уравнение которой f(x,y) = 0. Тогда моменты инерции этой фигуры находятся по формулам:
-
относительно оси ОХ:
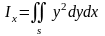(4.6.4)
-
относительно оси ОУ:
(4.6.5)
-
относительно начала координат:
.
(4.6.6)
5) Вычисление центров масс (тяжести) плоских фигур.
Координаты центра тяжести находятся по формулам:
(4.6.7)
где w – поверхностная плотность (dm = wdydx –масса элемента площади).
4.6.2 Приложение тройных интегралов.
1) Объемы тел.
Если поверхность тела описывается уравнением f(x, y, z) = 0, то объем тела может быть найден по формуле:
(4.6.8)
где х1 и х2– постоянные величины, у1=у1(х) и у2=у2(х), z1=z1(х,у) и z2 = z2(х,у).
2) Координаты центра тяжести тела.
(4.6.9)
3) Моменты инерции тела относительно осей координат.
(4.6.10)
4) Моменты инерции тела относительно координатных плоскостей.
(4.6.11)
5) Момент инерции тела относительно начала координат.
(4.6.12)
В приведенных выше формулах V – область вычисления интеграла по объему, w – плотность тела в точке (х, у, z), dv – элемент объема
в декартовых координатах: dv = dxdydz;
в цилиндрических координатах: dv = rdzdjdq;
в сферических координатах: dv = r2sinjdrdjdq.
4.6.3 Приложение криволинейных интегралов.
1) Длина дуги кривой.
Если
f(x,
y,
z)
= 1, то
=
(4.6.13)
где S – длина дуги кривой, - наибольшая из всех частичных дуг, на которые разбивается дуга АВ.
2) Теорема о среднем.
Если функция f(x, y, z) непрерывна на кривой АВ, то на этой кривой существует точка (x1, y1, z1) такая, что
. (4.6.14)
Лекция 7
Модуль 5. Дифференциальные уравнения.
Тема 5.1. Обыкновенные дифференциальные уравнения
1-го порядка.
5.1.1.Дифференциальные уравнения с разделяющимися переменными иоднородные дифференциальные уравнения 1-го порядка.
5.1.2. Линейные дифференциальные уравнения (ЛДУ)1-го порядка и уравнения Бернулли.
5.1.3.Уравнения в полных дифференциалах.