
- •Модуль 4. Функции нескольких переменных
- •Тема 4.1. Функции нескольких переменных.
- •4.1.1. Область определенияфункции нескольких переменных.
- •П римеры.
- •4.1.2. Предел функции нескольких переменных.
- •4.1.3. Непрерывность функции 2-х переменных.
- •Пример.
- •Тема 4.2.Частные производные и полный дифференциал.
- •Частные производные.
- •Пример 1
- •Пример 2
- •Типовой пример.
- •Дифференцирование сложных и неявных функций.
- •Типовые примеры. Пример 1.
- •Полный дифференциал.
- •Тема 4.3 Производная по направлению.
- •4.3.1 Производная по направлению.
- •Замечание
- •2) Линии и поверхности уровня.
- •4.3.2 Градиент.
- •4.3.3 Экстремум функции 2-х переменных.
- •Тема 4.4 Двойной интеграл
- •4.4.1 Двойной интеграл в декартовой системе координат (дск)
- •4.4.2. Двукратный интеграл.
- •4.4.3 Двойной интеграл в полярной системе координат (пск)
- •Тема 4.5 Тройной интеграл
- •4.5.1 Тройной интеграл в дск.
- •4.5.2.Тройной интеграл в цск и сск.
- •4.5.3 Криволинейный интеграл.
- •Тема 4.6Приложение кратных интегралов.
- •4.6.1 Приложение двойных интегралов.
- •4.6.2 Приложение тройных интегралов.
- •4.6.3 Приложение криволинейных интегралов.
- •Модуль 5. Дифференциальные уравнения.
- •Тема 5.1. Обыкновенные дифференциальные уравнения
- •5.1.1. Дифференциальные уравнения с разделяющимися переменными и однородные дифференциальные уравнения
- •5.1.2. Линейные дифференциальные уравнения (лду)
- •1) Понятие лду 1-го порядка. Определение 5.1.13.
- •2) Решение лду 1-го порядка.
- •5.1.3. Уравнения в полных дифференциалах.
- •Определение 5.1.15.
- •2) Решение уравнения в полных дифференциалах.
- •Тема 5.2. Линейные дифференциальные уравнения
- •5.2.1. Однородные линейные дифференциальные уравнения (лду)
- •5.2.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Общее решение.
- •5.2.3. Решение линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами методом вариации произвольных постоянных и методом решения в зависимости от вида правой части.
- •Тема 5.3. Системы обыкновенных дифференциальных уравнений1-го порядка
- •5.3.1. Основные понятия.
- •5.3.2. Метод характеристического уравнения.
- •5.6.3. Метод исключения.
- •Модуль 6. Ряды.
- •Тема 6.1. Числовые ряды.
- •6.1.1Необходимый признак сходимости ряда.
- •Найти сумму n первых членов ряда ( Sn ), и сумму ряда (s).
- •6.1.2. Достаточные признаки сходимости.
- •6.1.3. Знакочередующиеся и знакопеременные ряды.
- •Тема 6.2. Функциональные ряды.
- •6.2.1.Основные понятия.
- •6.2.2. Действия с функциональными рядами.
- •6.2.3.Степенные ряды.
- •Тема 6.3. Ряды Тейлора и Маклорена.
- •6.3.1. Ряд Тейлора.
- •6.3.2. Ряд Маклорена.
- •6.3.3. Биномиальный и логарифмический ряды.
4.5.2.Тройной интеграл в цск и сск.
Понятие тройного интеграла в цилиндрической системе координат (ЦСК).
Определение 4.5.3.
Тройным интегралом в ЦСКназывается интеграл, выраженный через цилиндрические координаты.
2)Замена переменных в тройном интеграле.
Операция замены переменных в тройном интеграле аналогична соответствующей операции для двойного интеграла.
Если x=x(u,v,w), y=y(u,v,w), z=z(u,v,w), (4.5.2)
то
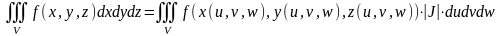 ,
(4.5.3)
,
(4.5.3)
где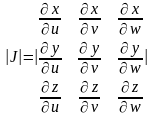 (4.5.4) - Якобиан.
(4.5.4) - Якобиан.
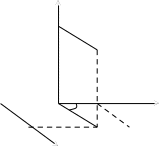
3) Цилиндрическая система координат.
 z
z
P
z
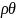 z
z
r
 х
х
Связь цилиндрической системы координат с декартовой системой осуществляется по формулам:
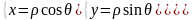

Для представления тройного интеграла в цилиндрических координатах используется Якобиан:

Итого:
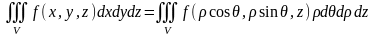
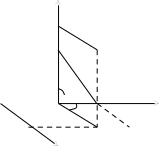
4)Сферическая система координат.
 z
z
r P
j
х
Связь сферической системы с декартовой осуществляется по формулам:
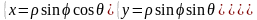

Для представления тройного интеграла в сферических координатах вычисляем Якобиан:
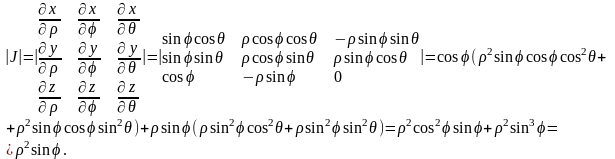 Окончательно
получаем:
Окончательно
получаем:

4.5.3 Криволинейный интеграл.
1) Криволинейный интеграл 1-го рода.
Определение 4.5.4.
Криволинейным интегралом первого рода по длине дуги АВ называется предел интегральной суммы при стремлении к нулю шага разбиения кривой:
 (4.5.5)
(4.5.5)
2) Вычисление криволинейного интеграла 1-го рода.
Кривая
АВ
задана уравнением
 .Криволинейный
интеграл по длине дуги АВ
находится по формуле:
.Криволинейный
интеграл по длине дуги АВ
находится по формуле:
 (4.5.6)
(4.5.6)
3) Криволинейный интеграл 2-го рода.
Определение 4.5.6.
Криволинейным
интегралом второго рода (или интегралом
по координатам) от функций
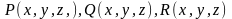 по кривой АВ
называется интеграл вида:
по кривой АВ
называется интеграл вида:
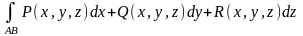 (4.5.7)
(4.5.7)
Замечание.
Криволинейный
интеграл по замкнутой кривой L
обозначается
 (4.5.8) и не зависит от выбора начальной
точки, а зависит только от направления
обхода кривой, которое задается
дополнительно. Если L
– замкнутая кривая без точек
самопересечения, то направление обхода
контура против часовой стрелки называется
положительным.
(4.5.8) и не зависит от выбора начальной
точки, а зависит только от направления
обхода кривой, которое задается
дополнительно. Если L
– замкнутая кривая без точек
самопересечения, то направление обхода
контура против часовой стрелки называется
положительным.
4) Вычисление криволинейного интеграла 2-го рода.
Контур
интегрирования АВ (плоская кривая)
задан уравнением y
= f(x),
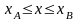 .
.
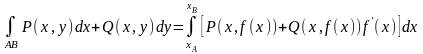 (4.5.9)
(4.5.9)
Типовой пример.
Вычислить
криволинейный интеграл
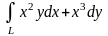 .
L–
контур, ограниченный параболами
.
L–
контур, ограниченный параболами
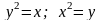 .
Направление обхода контура положительное.
.
Направление обхода контура положительное.
Решение.
Представим
замкнутый контур L
как сумму двух дуг L1
= x2
и
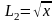
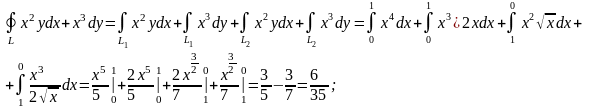
5) Вычисление криволинейного интеграла 1-го рода заданного параметрически.
Кривая АВ задана параметрическими уравнениями x = x(t), y = y(t), z = z(t), t, где функции х, у, z – непрерывно дифференцируемые функции параметра t, причем точкеА соответствует t = , а точке В соответствует t = . Функция f(x, y, z) – непрерывна на всей кривой АВ.
Криволинейный интеграл по длине дуги АВ находится по формуле:
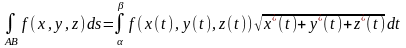 (4.5.10)
(4.5.10)
Типовой пример.
Вычислить
интеграл
 по одному витку винтовой линии
по одному витку винтовой линии
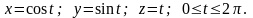
Решение.
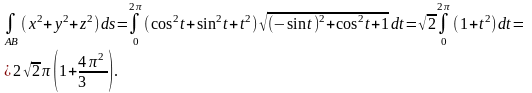
6) Вычисление криволинейного интеграла 2-го рода заданного параметрически.
Контур
интегрирования задан параметрически:
x=x(t),
y=y(t),
z=z(t),

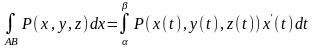 (4.5.11)
(4.5.11)
 (4.5.12)
(4.5.12)
 (4.5.13)
(4.5.13)
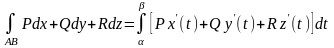 (4.5.14)
(4.5.14)
Лекция 6
