4.4.2. Двукратный интеграл.

1) Понятиедвукратного интеграла в ДСК.

Определение 4.4.2.

Двукратным или повторным интегралом от функции f(x, y), непрерывной в замкнутой области D, ограниченной линиями х = a, x = b, (a<b), y = j(x), y=y(x), где j и y - непрерывные функции и j£yназывается интеграл вида

(4.4.2.)

Определение 4.4.3.

Область, границу которой любая прямая параллельная оси ох пересекает только в двух точках, называется правильной в направлении оси ох. Область правильная во всех направлениях называется правильной областью.

Замечание.

1. Двукратные интегралы вычисляются по правильным областям.

2. Если область неправильная, она разбивается на несколько правильных областей.

2) Правило вычисления двукратного интеграла.

Сначала вычисляется внутренний интеграл при условии, что х принимается за константу. Затем полученный результат ставится внутрь внешнего интеграла. Полученный внешний интеграл зависит только от х и он вычисляется как обычный определенный интеграл.

Типовые примеры.

Пример 1.

Вычислить интеграл по области D, ограниченной линиями y = x, x = 0, y=1, y = 2.

Решение.

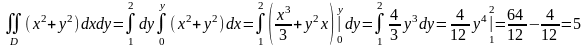
Пример 2.

Вычислить интеграл по области, ограниченной линиями ху=1,

у = , х = 2.

Решение.

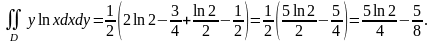
3) Замена переменных в двойном интеграле.

Рассмотрим двойной интеграл вида , где переменная х изменяется в пределах от a до b, а переменная у – от у₁(x) до у₂(х).Положим х= х(u,v),y = у(u,v). Тогда dx = ,dy= и интеграл примет вид ,

где называется определителем Якоби или Якобианом.

4.4.3 Двойной интеграл в полярной системе координат (пск)

1) Понятиедвойного интеграла в ПСК.

Определение 4.4.4.

Двойным интегралом в ПСК называется двойной интеграл вида 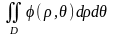(4.4.3.), где координаты ПСК, причём переменная изменяется в пределах от до .

2) Замена переменных в двойном интеграле.

Рассмотрим двойной интеграл вида , где переменная х изменяется в пределах от aдо b, а переменная у – от у₁(x) до у₂(х).

Положим х = х(u, v); y = у(u, v)

Тогда dx = ; dy = ; (4.4.4.)

, (4.4.5.)

где (4.4.6.) называется определителем Якоби или Якобианом.

3) Двойной интеграл в полярной системе координат (ПСК).

Координаты в декартовой системе связаны с координатами в полярной системе следующими соотношениями:

Переход от декартовой к полярной системе координат осуществляется по формуле замены переменных:

(4.4.7.)

В этом случае Якобиан имеет вид:

(4.4.8.)

Тогда (4.4.9.)

Здесь (4.4.10.)

4) Вычисление двойного интеграла с помощью преобразования из ДСК в ПСК.

Типовой пример.

Вычислить двойной интеграл c помощью перехода к полярным координатам, если D – первая четверть круга .

Решение.

Лекция 5

Тема 4.5 Тройной интеграл

4.5.1 Тройной интеграл в ДСК.

4.5.2 Тройной интеграл в ЦСК И ССК.

4.5.3 Криволинейный интеграл.

4.5.1 Тройной интеграл в дск.

1) Понятиетройного интеграла в ДСК.

Определение 4.5.1.

Тройным интегралом в ДСК называется предел интегральной суммы , (4.5.1.)

где v- область, которая ограничена некоторой поверхностью j(x, y, z) = 0.

2) Понятие повторного трёхкратного интеграла в ДСК.

Определение 4.5.2.

Повторным трёхкратным интегралом в ДСК называется интеграл вида

гдех₁ и х₂ – постоянные величины, у₁=у₁(х) и у₂=у₂(х), z₁=z₁(х,у) и z₂ = z₂(х,у).

3)Расстановка пределов интегрирования.

Если область v определена неравенствами х₁ х х₂, гдех₁ и х₂постоянные величины, у₁(х) у у₂(х), z₁(х,у) z z₂(х,у) – функции от одной и двух переменных, то пределы интегрирования расставляются соответственно.

4) Вычисление повторного интеграла в ДСК.

Интеграл, берущийся по z, называется внутренним, по у – промежуточным, по х – внешним. Вычисляется вначале внутренний интеграл, затем промежуточный, затем внешний.

5) Расчёт тройного интеграла в ДСК.

Вначале тройной интеграл преобразуется в трёхкратный. Затем вычисляется трёхкратный интеграл. Результат считается результатом тройного интеграла.

Типовой пример.

Вычислить интеграл

Решение.