Тема 4.3 Производная по направлению.
Градиент. Экстремум.
4.3.1 Производная по направлению.
4.3.2.Градиент.
4.3.3 Экстремум.
4.3.1 Производная по направлению.
1) Скалярное поле.
Определение 4.3.1.
Если в области D задана скалярная функция в точке Р, т.е.U =U(P), то говорят что в этой области задано скалярное поле.
Замечание
Точка
Р
будет определяться скалярными аргументами
если в системе X0Y
,
а если в системе X0YZP=P(x,y,z).
И
(4.3.1.) будет определяться как скалярная
функция скалярного аргумента, а множество
значений таких функций будет называться
скалярным полем.
Примеры скалярных полей: 1) поле температур, 2) поле давлений, 3) поле солёности моря.
2) Линии и поверхности уровня.
Определение 4.3.2.
Линией уровня
скалярного поля называется геометрическое
место точек, в которых функция
принимает постоянное значение, а
поверхностью уровня скалярного поля
называется геометрическое место точек,
в которых функция
принимает постоянное значение.
Примеры.
1.
(окружность) - линия уравнения.
2.
(эллипсоид) – поверхность уровня.
3)Направление косинусы.
Рассмотрим
функцию u(x,
y,
z)
в точке М( x,
y,
z)
и точке М1(
x
+ Dx,
y
+ Dy,
z
+ Dz).
Проведем через точки М и М1
вектор
.
Углы наклона этого вектора к направлению
координатных осей х, у, z
обозначим соответственно a,
b,
g.
Косинусы этих углов называются
направляющими косинусами вектора
. Расстояние
между точками М и М1
на векторе
обозначим DS:
(4.3.4). Тогданаправляющие
косинусы равны
(4.3.5.)
4)Производная по направлению.
Пусть
функция u(x,
y,
z)
непрерывна и имеет непрерывные частные
производные по переменным х, у и z.
Тогда ее полное приращение представимо
в виде:
,где
величины e1,
e2,
e3
– бесконечно малые при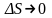
.
Так
как
то 
;
(4.3.6)
Определение 4.3.3.
Предел
называется производной функции u(x,
y,
z)
по направлению вектора
в точке с координатами (x,y,z).
Замечание.
В
случае z
= z(x,y)
(4.3.7)
Типовой пример.
Вычислить
производную функции z
= x2
+ y2x
в точке А(1,
2) по направлению
вектора
,
гдеВ (3, 0).
Решение.
Координаты
вектора
:
=(3-1;
0-2) = (2; -2) = 2
.Длина
(модуль) этого вектора:
=
,
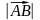значения
частных производных в точке А
:
=
Отсюда получаем значения направляющих косинусов вектора :
cosa
=
;
cosb
= -
Окончательно
получаем:
- значение производной заданной функции
по направлению вектора
.
4.3.2 Градиент.
1) Градиент
Определение 4.3.4.
Градиентом функции
u
называется вектор вида
(4.3.8)
При этом говорят, что в области D задано поле градиентов.
Теорема 4.3.1.
равняется проекции
вектора gradu
на вектор
:
(4.3.9)
Следствие.
.
(4.3.9а)
Типовой пример.
Найти производную функции z=ln(x2+y2) в точке M(3;4) в направлении градиента функции z.
Решение:
Вектор s совпадает с градиентом функции z=ln(x2+y2) в точке M(3;4) и равен
grad
z=
=
Следовательно,
2) Частные производные высших порядков.
Определение 4.3.5.
Частными производными n-ого порядка называются частные производная первого порядка от частных производных (п-1)-го порядка.
Примеры.
3) Дифференциалы высших порядков
Определение 4.3.6.
Дифференциаламиn-ого порядка называются дифференциалы первого порядка от дифференциалов (п-1)-го порядка.
Примеры.
(4.3.10)
…………………
(4.3.11)