Найти сумму n первых членов ряда ( Sn ), и сумму ряда (s).

Решение.

Ответ: S_n= , S= 1.

2. Основные теоремы.

Теорема 6.1.1.

На сходимость ряда не влияет отбрасывание конечного числа его членов.

Теорема 6.1.2.

Если ряд а₁ + а₂ + ……………… + а_п + ……сходится и его суммой является S, то сходится и ряд са₁ +с а₂ + ………… +с а_п +…и его суммой является сS.

Теорема 6.1.3.

Если сходится ряд а₁ + а₂ + ……………… + а_п + …… и его суммой является S,

и сходится ряд b₁ +b₂ + ……………… + b_п + …… и его суммой является , то

сходится и ряд (а₁ + b₁)+ (а₂ + b₂)+ ……………… +( а_п + b_п)+ …… и его суммой является S+

2. Необходимый признак сходимости ряда.

Теорема 6.1.4.(Необходимый признак сходимости ряда)

Если ряд (6.1.1.) сходится, то

6.1.2. Достаточные признаки сходимости.

1) Достаточные признаки сходимости знакоположительных рядов

Признак, гарантирующий достоверный ответ на вопрос о сходимости или расходимости числового знакоположительного ряда, называется достаточным признаком сходимости ряда.

2. Признак сравнения.

Теорема 6.1.5.

Если члены рядаа₁ + а₂ + ……………… + а_п + …… (6.1.1) не превосходят члены ряда b₁ +b₂ + ……………… + b_п + ……(6.1.3)т.е. а_п≤ b_п, (6.1.4) тоиз сходимости (6.1.3) следует сходимость (6.1.1), и из расходимости (6.1.1) следует расходимость (6.1.3).

Теорема 6.1.6.

Если существует конечный и отличный от нуля предел (в частности, если a_n ~ b_n), то ряды сходятся или расходятся одновременно.

Типовые примеры.

Пример 1.

Определить сходимость ряда

Решение.

Данный ряд сходится, так как a_n= , причем геометрическая прогрессия , знаменатель которой q= , сходится.

Пример 2.

Определить сходимость ряда .

Решение.

Этот ряд расходится, так как его общий член больше соответствующего члена гармонического ряда (который расходится).

Пример 3.

Определить сходимость ряда .

Решение.

Ряд расходится, так как ( : )= ≠0, а гармонический ряд (то есть ряд с общим членом ) расходится.

Пример 4.

Определить сходимость ряда .

Решение.

Ряд сходится, так как ( : )= 1, т.е. ~ , а ряд с общим членом сходится.

3) Признак Даламбера.

Теорема 6.1.7.

Если для ряда (6.1.1) существует конечный предел , то

если l< 1 ряд (6.1.1) сходится,

если l> 1 ряд (6.1.1) расходится,

если l= 1, то заключение о сходимости или расходимости ряда (6.1.1) сделать нельзя, требуются дополнительные исследования.

2. Радикальный признак Коши.

Теорема 6.1.8.

Если для ряда (6.1.1) существует конечный предел 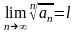, то

если l< 1 ряд (6.1.1) сходится,

если l> 1 ряд (6.1.1) расходится,

если l= 1, то заключение о сходимости или расходимости ряда (6.1.1) сделать нельзя, требуются дополнительные исследования.

2. Интегральный признак Коши.

Теорема 6.1.9.

Если члены ряда (6.1.1) положительны и не возрастают, т.е.

а₁≥ а₂≥ ……………… ≥ а_п ≥ …и формула общего члена а_п= f(n) представляет собой непрерывную, невозрастающую функцию, то

если - сходится, то сходится и ряд (6.1.1),

если - расходится, то расходится и ряд (6.1.1).