Лекция 1.

Модуль 4. Функции нескольких переменных

Тема 4.1. Функции нескольких переменных.

4.1.1. Область определенияфункции нескольких переменных.

4.1.2. Пределфункции нескольких переменных.

4.1.3. Непрерывность функции 2-х переменных.

4.1.1. Область определенияфункции нескольких переменных.

1. Понятие функции нескольких переменных.

Определение 4.1.1.

Определение 4.1.1.

Величина y называется функцией независимых переменных величин x₁; x₂;… x_n, называется аргументированной, если каждой конкретной совокупности этих аргументов соответствуют определенные значения y.

2. Способы задания.

а) аналитический (в виде формул), например, Z = x² + y²;

б) графический; в) табличный.

2. Область определения функции нескольких переменных.

Определение 4.1.2.

Совокупность всех значений аргументов, при которых функция определена, называется областью определения или областью существующей функции.

П римеры.

Такая область существования называется замкнутой.

Такая область существования называется незамкнутой или открытой.

4) Геометрическая интерпретация функции двух переменных.

z

Примеры.

Z = x² + y²

α

0

y

x

Параболоид вращения (однополосный)

5) Линии и поверхности уровня.

Определение 4.1.3.

Линией уровня функции Z = Z(x;y) называется линия Z(x;y)=C на плоскости x0y.

П ример.

Z = x² + y²

x²+ y² = C – окружность радиуса .

Определение 4.1.4.

Поверхностью уровня функции u=u(x,y,z) называется поверхность u(x,y.z)=c в системе координат .

Типовой пример.

u = x² + y²+z². Требуется определить для неё поверхность уровня.

Решение.

Для неё поверхностью уровня x² + y² +z²=c будет сфера радиуса .

4.1.2. Предел функции нескольких переменных.

1) Частное и полное приращение функции двух переменных.

Определение 4.1.5.

Частным приращением функции Z = Z(x;y) называют приращение которое получает эта функция при частном приращении одного из его аргументов.

Определение 4.1.6.

Полным приращением функции Z = Z(x;y) называют приращение, которое получает эта функция при приращении всех его аргументов

2) Понятие δ - окрестности функции.

Определение 4.1.7.

δ - окрестностью точки называется совокупность всех точек 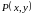лежащих внутри кривой радиуса δ, удовлетворяющих неравенству

3) Понятие предела функции 2-х переменных.

Определение 4.1.8

Число А называется пределом функции при , если для любого существует такое , что как только . . (4.1.5)

Типовой пример.

4.1.3. Непрерывность функции 2-х переменных.

1) Понятие непрерывности функции 2-х переменных.

Определение 4.1.9.

Функция Z = Z(x;y) называется непрерывной в точке принадлежащей области определения функции, если

Определение 4.1.10.

Функция Z = Z(x;y) называется непрерывной в точке , если

lim (4.1.7.), где (4.1.8.)

(4.1.9)

Определение 4.1.11.

Функция непрерывная в каждой точке области D называется непрерывной в области D.

2) Понятие разрывности функции 2-х переменных.

Определение 4.1.12.

Если функция Z = Z(x;y) не является непрерывной в точке , то она в этой точке является разрывной, а сама точка называется точкой разрыва.

3) Типы точек разрыва.

1)) Функция Z = Z(x;y) определена во всех точках некоторой окрестности точки за исключением самой этой точки.

Пример.

2)) Z = Z(x;y) определена во всех точках некоторой окрестности , но - не существует.

Пример.

Покажем, что предел этой функции не существует

При k=1 этот предел равен нулю, при k=0 – единице и т. д., то есть конкретного предела не существует.

2. Z = Z(x;y) определяется во всех точках некоторой окрестности и предел существует, но ≠