1.5 Пример вычислений

Исходные данные: P₁=15 %, P₂=30 %, P₃=0.80 %,

Для оценки качества пшеничной муки необходимо определить следующие показатели: влажность, клейковину и зольность. Эти показатели определяют, исходя из технологической цели процесса, например, для муки высшего сорта из твёрдой пшеницы: влажность Р1min ÷ Р1max = 5 ÷ 15,5 %; клейковина Р2min ÷ Р2max = 10 ÷ 30 %; зольность Р3min ÷ Р3max = 0,25 ÷ 0,75 %.

Коэффициенты весомости относительных показателей качества: M1=0.2; M2=0.3; M3=0.5, .

Зависимость между абсолютной величиной единичного показателя качества и относительным значением определяется:

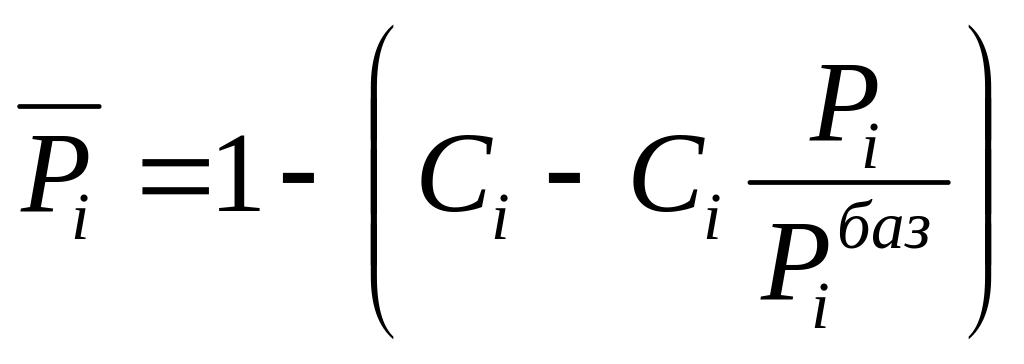
Находим относительное значение показателя влажности:

= = =

=

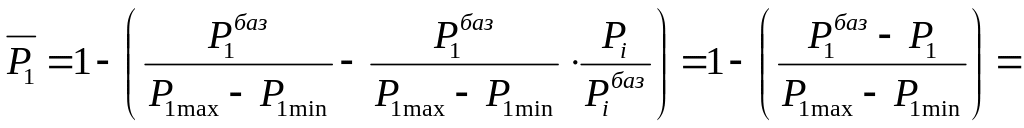
Находим относительное значение показателя клейковины:

=

Находим относительное значение показателя зольности:

=

=

Находим взвешенное среднеарифметическое значение:

= =

Находим взвешенное среднегеометрическое значение:

= =

= 1.05

Определяем взвешенную среднегармоническую оценку:

=

=

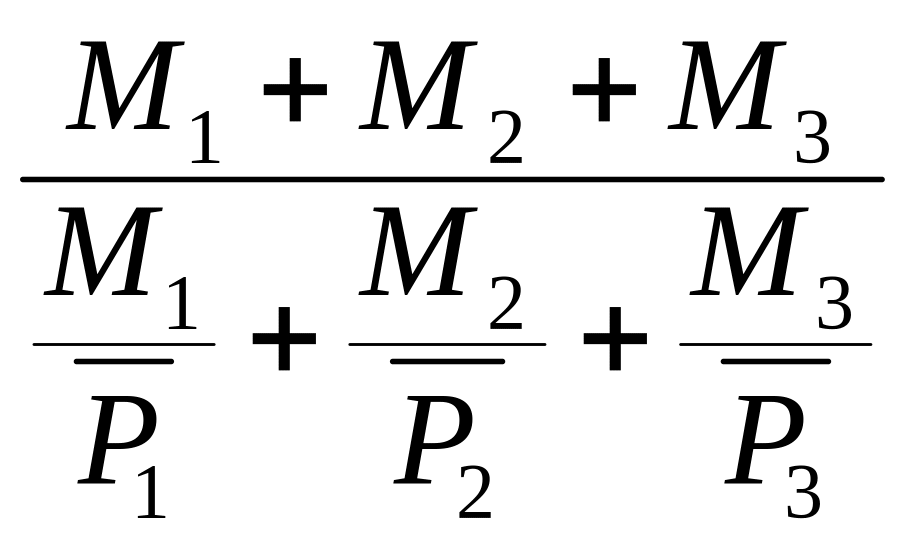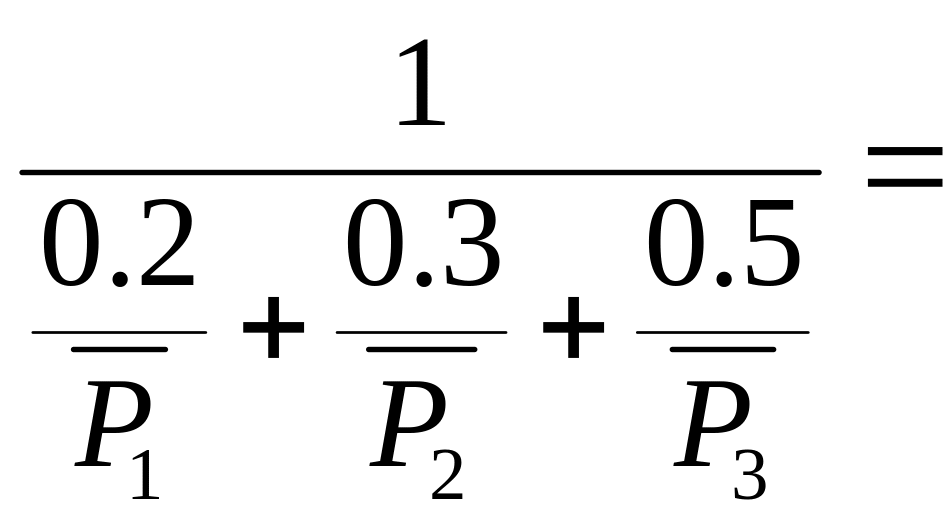
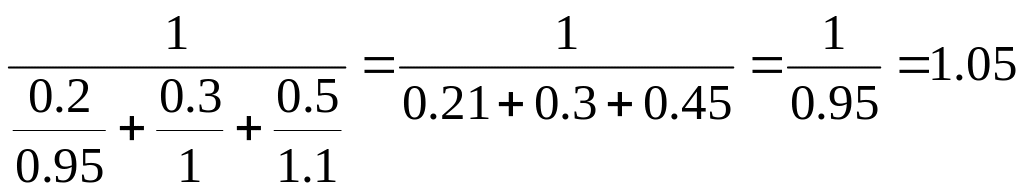
Таким образом,

, , , Р_са = 1.04, Р_сг=1.05, Р_сгарм=1.05

1.6 Контрольные вопросы

1.6.1 Что понимается под качеством продукции.

1.6.2 Дать понятие об абсолютном и относительном единичном показателе качества продукции.

1.6.3 Назовите и дайте характеристику основным методам, которые используются для измерения и оценки уровня качества продукции.

1.6.4 Формы комплексного показателя качества продукции и соотношения для их вычисления.

1.6.5 Расскажите об обобщённом показателе качества. Приведите примеры.

1.6.6 Роль коэффициентов весомости при определении качества продукции.

2 Изучение и оценка точности функционирования технологического потока

2.1 Цель работы

Изучить показатели, которыми оценивается точность функционирования тех­нологических потоков, а также научиться вычислять и оценивать основные пока­затели точности.

2.2 Краткие теоретические сведения

Точность функционирования технологического потока представляет собой степень соответствия поля рассеяния показателя качества продукции заданному полю допуска и его расположению. Точность оценивается рядом количественных показателей: коэффициентом соответствия, коэффициентом смещения и вероятно­стью или процентом выхода годных изделий. Под годными изделиями понимают изделия, показатели качества которых находятся в пределах установленного поля допуска. Выход годных изделий определяется величиной систематической и слу­чайной составляющих производственной погрешности.

К систематическим погрешностям относятся те, которые вызываются постоянно действующими факторами. Например, при проведении замеса теста систематические погрешности будут вноситься: температурой и влажностью окружающей среды, изменением частотой вращения рабочих органов, продолжительностью замеса и т.д. Эти погрешности относительно просто учитываются, так как они постоянны.

К случайным погрешностям относятся те, которые вызваны действием не постоянных факторов. Например, при проведении замеса теста возможно колебание качества муки, поступающей в производство, несоблюдение условий проведения замеса и т.д. Попытка сниже­ния этой погрешности, как правило, не достигает цели. Однако для повышения эффективности производства необходи­мо уменьшать и неизбежное рассеяние показателей качества продук­ции.

Рост количества дефектной продукции иногда происходит по при­чине грубых ошибок обслуживающего персонала или аварий оборудо­вания. Такие погрешности в функционировании технологической системы при оценке её точности не учитываются. Отклонение величин показателей качества продук­ции от стандарта, как правило, есть результат наложения всех перечисленных выше погрешностей.

Производственную погрешность по экспериментальным данным, в общем виде, можно представить в виде кривой плотности вероятности распределения (рисунок 2.1). Здесь е – отклонение центра группирования погрешностей и, в частности, среднего зна­чения Х_ср от номинала Х₀, характеризующее систематическую составляющую производственной погрешности; (Х_max – Х_min) – поле рассеяния, характеризующее случайную составляющую производственной погрешности.

Рисунок 2.1 – График плотности вероятности показателя качества изделий

Систематическую составляющую производственной погрешности можно оценить коэффициентом смещения Е:

, (2.1)

где е = |Х_ср-Х₀| - величина смещения, зависящая от положения центра группирования производственной погрешности Х_ср;

Х₀ - номинальное значение показателя качества продукции, расположенное в идеале в середина поля допуска;

d - абсолютная величина половины поля допуска на показатель качества продук­ции.

На рисунке 2.2 показано распределение погрешностей показателя качества продукции, подчиняющихся нормальному закону распределения случайных вели­чин при одинаковой величине случайной погрешности, но при разных значениях коэффициента смещения. Чем ближе к нулю величина коэффициента смещения Е, тем меньше влияние систематической погрешности и выше точность функциони­рования технологического потока.

Действие случайной составляющей производственной погрешности оценива­ется коэффициентом соответствия Т:

, (2.2)

где d - абсолютная величина половины поля допуска на показатель качества из­делия;

s - среднее квадратичное отклонение показателя качества продукции в вы­борке;

К_р - коэффициент, зависящий от закона распределения погрешностей показателя качества изделий (таблица 2.1).

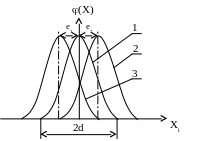
Рисунок 2.2 – Графики плотности вероятности показателя качества изделий при различных коэффициентах смещения: 1 – Е=0; 2 – Е0; 3 - Е0

Таблица 2.1 - Коэффициент К_р для основных законов распределения

Наименования закона распределения производственной погрешности	Коэффициент Кр
Нормальный закон	6
Закон Максвелла	5.25
Равномерный закон	3.46

Закон нормального распределе­ния случайных величин является наиболее распространённым для оценки производственных пог­решностей. При совершенствовании технологических процессов и раз­работке автоматизированных систем управления технологическим по­током (АСУТП) стремятся получить закон нормаль­ного распределения погрешностей параметров качества изделий, так как при хорошей технологической дисциплине, налаженном и устой­чивом потоке этот закон является объективным показателем высоко­го качества данной системы.

На рисунке 2.3 приведено распределение производственной погрешности по­казателя качества продукции, подчиняющегося нормальному закону при различных полях рассеяния погрешностей 6s, величинах коэффициента соответствия Т, заданных поле допуска 2d и центре группирования погрешностей х, совпадающем с серединой поля допуска, одинаковом коэффициенте смещения (Е=0). При Т>1 поток функционирует с высокой точностью, поскольку имеется за­пас точности. При Т=1 поле допуска совпадает с границами кривой плотности вероятности распределения показателя качества изделий и в любой момент могут появиться дефектные изделия. И, наконец, при Т<1 дефектные изделия имеются в результате функционирования технологического потока.

Все три параметра точности технологического потока: процент выхода год­ных изделий Р_г, коэффициент смещения Е и коэффициент соответствия Т между собой взаимосвязаны. На практике для расчёта точности функционирования ис­пользуют таблицы, из которых по известным двум показателям находят третий. В приложении приведена таблица Р_г(Е,Т) для нормального закона

Рисунок 2.3 – Графики плотности вероятности показателя качества изделия при различных коэффициентах соответствия: 1 – Т>1; 2 – T=1; 3 – T<1

распределения с изменением Т в диапазоне от 0.10 до 1.50 и Е в диапазоне от 0.00 до 0.50.

Параметры точности учитывают не просто соотношение между полем допус­ка показателя качества продукции и полем рассеяния производственной погреш­ности, но и закон их распределения, что очень важно, поскольку знание закона распределения производственной погрешности, а не только границ поля её рассея­ния, способствует выявлению физической сущности погрешности технологического процесса, приводящей к тому или иному распределению.