5.3 Порядок выполнения работы
Имеются данные об отказах по пяти объектам, взятые из журнала эксплуатации, которые функционировали в течении недели (таблица 5.1).
Таблица 5.1 – Исходные данные для расчёта надёжности функционирования
Номер объекта |
Время отказа, мин |
Объект № 1 |
32,52,142,262,322,502,542,822,832,891,1007,1086,1326,1356, 1367,1389,1416,1480,1605,1615. |
Объект № 2 |
43,48,67,76,142,203,285,420,508,566,783,809,1052,1052,1098, 1101,1155,1180,1319,1331,1417. |
Объект № 3 |
30,108,179,248,281,358,409,511,592,663,895,937,957,980, 1144,1168,1301,1450,1501,1531. |
Объект № 4 |
135,170,253,271,325,406,507,595,689,713,750,907,1016,1081, 1229,1350,1371,1387,1430,1460. |
Объект № 5 |
83,121,231,359,411,489,507,565,701,790,905,936,1033,1091, 1206,1289,1291,1341,1433,1517. |
5.3.1 Определяем значения случайных величин и размах. В данном случае случайной величиной является наработка на отказ, т.е. чистое время работы системы от отказа до отказа. Для этого необходимо вычесть из каждого предыдущего значения момента времени отказа каждое последующее. Первые значения моментов времени отказов для каждого из пяти объектов остаются без изменений, поскольку предыдущих значений нет (таблица 5.2).
Таблица 5.2 – Наработки на отказ по всем объектам
Номер объекта |
Наработка, мин |
Объект № 1 |
32,20,90,120,60,170,40,280,10,59,116,79,240,30,11,22,27 64,125,10. |
Объект № 2 |
43,5,19,9,66,61,82,135,88,58,217,26,243,46,3,54,25,139,12, 86. |
Объект № 3 |
30,79,69,33,77,51,102,81,71,232,42,20,22,23,164,24,133, 149,51,30. |
Объект № 4 |
135,35,83,18,54,84,98,88,94,24,37,157,109,65,148,121,21, 16,43,30. |
Объект № 5 |
83,38,110,128,52,78,18,58,136,89,115,31,97,58,115,83,2, 50,92,84. |
Для определения размаха строим вариационный ряд случайной величины (таблица 5.3).
Таблица 5.3 – Вариационный ряд наработки на отказ
-
2
3
5
9
10
10
11
12
16
18
18
19
20
20
21
22
22
23
24
24
25
26
27
30
30
30
30
31
32
33
35
37
38
40
42
43
43
46
50
51
51
52
54
54
58
58
58
59
60
61
64
65
66
69
71
77
78
79
79
81
82
83
83
83
84
84
86
88
88
89
90
92
94
97
98
102
109
110
115
115
116
120
121
125
128
133
135
135
136
139
148
149
157
164
180
217
232
240
243
280
Максимальное значение случайной величины равно 280 мин, а минимальное значение 2 мин. Следовательно, размах вариационного ряда R= 280-2 = 278 минут.
5.3.2 Для построения гистограммы и полигона частостей случайной величины необходимо разделить размах варьирования случайной величины на равные интервалы и определить частоту попадания значений случайной величины в каждый интервал. Количество интервалов определяем по выражению:
, (5.1)
где r – число равных интервалов разбиения вариационного ряда;
n – число значений случайной величины, составляющих вариационный ряд.
.
Эта выражение даёт 8 интервалов, следовательно, размах каждого интервала
.
Округляем полученную величину до целого числа, получаем 35.
5.3.3 Составляем таблицу распределения частоты и частостей по интервалам (таблица 5.4).
Если значения случайных величин попали на границу интервала, то необходимо разделить их между двумя соседними интервалами пополам.
По данным таблицы 5.4 (первая и пятая графы) строим гистограмму и полигон частостей, т.е. график вероятности появления случайной величины (рисунок 5.1). Затем строим эмпирическую функцию вероятности отказов (первая и третья) (рисунок 5.2).
Таблица 5.4 – Распределение наработки на отказ
-
Границы интервалов
Частота ni
Частость ni/n
Накопленная частота, ni
Накопленная частость, ni/n
2-37
31,5
0,315
31,5
0,315
37-72
223,5
0,235
55
0,550
72-107
21
0,210
76
0,760
107-142
14
0,140
90
0,900
142-177
4
0,040
94
0,940
177-212
1
0,010
95
0,950
212-247
4
0,040
99
0,990
247-280
1
0,010
100
1,000
Рисунок 5.1 – Гистограмма и полигон частостей наработки на отказ
Рисунок 5.2 – Эмпирическая функция вероятности отказов
5.3.4 Используя данные таблицы 5.3, определяем среднее значение случайной величины:
,
(5.2)
где Тi – наработка на отказ (таблицы 5.3);
n – число учитываемых наработок на отказ (число величин составляющих вариационный ряд таблицы 5.3).
Если в формулу 5.2 подставить числовые значения для данного примера, то получим Тср= 74,88 мин.
5.3.5 Определяем значение дисперсии распределения случайной величины:
.
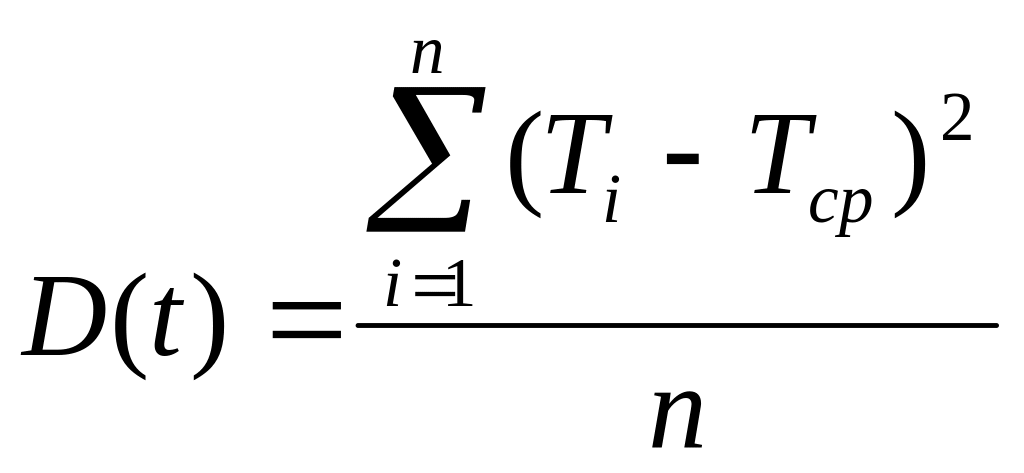(5.3)
В данном случае она равна D(t) = 3132,5 мин2.
5.3.6 Рассчитаем значение стандартного отклонения распределения случайной величины:
мин.
5.3.7 Рассчитаем значение коэффициента вариации случайной величины:
мин.
5.3.8 Находим ошибку в определение стандартного отклонения распределения случайной величины:
мин.
Тогда Тср = 74,88 5.6 мин, или округляя 69 Тср 81.
5.3.9 Поскольку ломанная кривая на рисунке 5.1 близка к экспоненте, а коэффициент вариации близок к единице, можно сделать предположение, что эмпирическое распределение является экспоненциальным.
5.3.10 Проверяем предположение о виде эмпирического распределения случайной величины на основе его линеаризации.
Проверка состоит в том, что по результатам испытаний, гипотеза относительно вида распределения должна быть принята как истинная или отброшена как должная. Таким образом, здесь говорится о согласованности теоретического распределения и экспериментальными данными.
На координатной плоскости соответствующей предполагаемому экспоненциальному распределению, наносим по данным таблицы 5.4 экспериментальные точки функции надёжности.
Затем убеждаемся в возможности линейного аппроксимирования. Проводим прямую линию так, чтобы отклонения экспериментальных точек от этой линии были минимальными (рисунок 5.3).
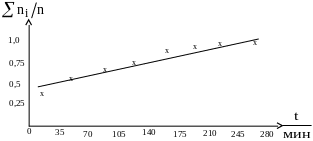
Рисунок 5.3 - Эмпирическая функция вероятности отказов соответствующая экспоненциальному распределению
Соответствие
теоретического распределения
экспериментальным данным можно проверить
с помощью критерия согласия Колмогорова.
Теоретическое распределение не
противоречит экспериментальным данным,
если
,
где Д
– максимальное значение модуля отклонения
теоретической функции распределения
от экспериментальной, n
– число испытаний (т.е. число величин,
составляющих вариационный ряд), которое
должно быть
.
Величина Д
измеряется в долях ординаты как расстояние
между наиболее удалёнными точкой и
прямой.
В
нашем случае Д = 0,01. Вычисляем значение
.
Это значение меньше 1. Поэтому можно
считать, что экспоненциальное распределение
наработки на отказ не противоречит
экспериментальным данным.
Параметр потока отказов определяется из выражения:
.
(5.4)
Подставляя
в формулу (5.4) значение Тср=
74.88 мин, получаем
=
мин
–1.
5.3.11 Аппроксимирующие математические выражения для плотности распределения по экспоненциальному закону
;
(5.5)
для функции вероятность отказов
;
(5.6)
для функции вероятности безотказной работы
.
(5.7)
Подставляя параметр потока отказов и различное значение времени в эти выражения, получим вероятности отказа и безотказной работы технологической системы (таблица 5.5).
Таблица 5.5 – Вероятности отказа и безотказной работы технологической системы
Время, t, ч |
F(t) |
P(t) |
0 |
0 |
1 |
25 |
0,28 |
0,72 |
50 |
0,50 |
0,50 |
75 |
0,60 |
0,40 |
100 |
0,70 |
0,30 |
150 |
0,80 |
0,14 |
200 |
0,93 |
0,07 |
250 |
0,96 |
0,04 |
300 |
0,98 |
0,02 |
5.3.12 Строим графики F(t) и P(t) (рисунок 5.4). Из графиков следует, что технологическая подсистема имеет весьма низкую надёжность, поскольку вероятность безотказной работы P(t) = 0,72 при t = 25 ч., а P(t) = 0,5 при t = 50 ч.
5.3.13 Основные показатели надёжности оцениваемой подсистемы приведены в таблице 5.6.
Составить отчёт по проделанной работе, в которую должны войти следующие разделы:
название и цель работы;
краткие теоретические сведения с основными соотношениями;
вычисление вероятности отказов F(t) и вероятности безотказной работы P(t) технологической системы;
выводы по проделанной работе.
Таблица 5.6 – Сводная таблица результатов расчёта надёжности
Показатели надёжности |
Значения показателей |
P(t=50) |
0,50 |
P(t=100) |
0,30 |
P(t=150) |
0,14 |
|
1310-3 мин-1 |
Tcp |
74,88 5,6 мин |
Рисунок 5.4 – График функции вероятности отказов F(t) и вероятности безотказной работы P(t) технологической системы