Тема 3.8. Модифицированный фильтр Калмана
Модифицированный (или квазилинейный [ ]) фильтр Калмана (МФК) является вариантом фильтра Калмана (ФК), предназначенным для оценки состояния нелинейных динамических систем с гладкими нелинейностями.
Этот фильтр широко используется в системах навигации ЛА, в том числе в системах навигации динамических объектов с помощью спутниковых навигационных систем.
Постановка задачи. Рассматривается нелинейная динамическая система, движение которой описывается векторным нелинейным уравнением состояния:
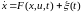. (3.45)
Движение
этой системы можно описать с помощью
математической модели с дискретным
временем, изменяющимся с шагом
:
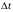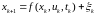, (3.46)
где
.
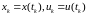При малом шаге от уравнения (3.45) с непрерывным временем можно перейти к уравнению (3.46) с дискретным временем, используя, например, метод численного интегрирования по формуле Эйлера:
,
а
непрерывный процесс
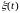заменив его приближенным аналогом с
дискретным временем: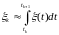 
.
В дискретные моменты времени проводятся измерения
. (3.47)
В соотношениях (3.46) и (3.47) и – векторные дискретные белые шумы с нулевыми математическими ожиданиями и заданными диагональными ковариационными матрицами и соответственно.
Требуется, зная априорную оценку состояния системы , ковариационную матрицу этой оценки , ковариационные матрицы и и располагая измерениями , , получить оценки состояния системы в моменты поступления этих измерений.
Решение.
В МФК нелинейная функция
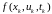в правой части уравнения состояния с
дискретным временем (3.46) используется
для прогнозирования
состояний системы между измерениями,
а нелинейная функция
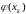- для расчета прогнозируемых
значений измерений.
Но эти нелинейные
функции не могут
быть использованы
непосредственно для прогнозирования
ковариационной
матрицы ошибок оценки состояния, так
как они должны быть линейными. Для этого
в МФК используются матрицы частных
производных от функций
и
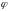по переменным вектора состояния
,
вычисляемые в окрестности текущего
прогнозируемого
состояния системы
,
т.е. происходит линеаризация
нелинейных функций в окрестности текущей
прогнозируемой оценки.
В результате МФК объединяет следующие соотношения прогноза и пересчета оценок, как обычно, применяемые поочередно:
а) Соотношения прогноза
- прогноз состояния:
; (3.48)
- прогноз ковариационной матрицы:
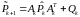, (3.49)
где
-
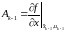матрица частных производных от
вектор-функции
по компонентам вектора
размерности
.
б) Соотношения пересчета
- расчет поправки к измерению, т.е. разности между проведенным измерением и его прогнозируемым значением:
;
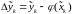- расчет поправки к ковариационной матрице
;
где
-
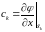матрица размерности
частных производных от нелинейной
вектор-функции
по компонентам вектора
;
- расчет матрицы Калмана:
;
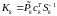- пересчет оценки вектора состояния:
;
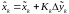(3.50)
- пересчет ковариационной матрицы ошибок в оценках компонент вектора состояния:
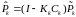. (3.51)
Достоинства и недостатки МФК. Основным достоинством МФК является возможность приближенного учета гладких нелинейностей в уравнениях состояния и измерений в системе.
Недостатком МФК является то, что, в отличие от стандартного ФК, модифицированный ФК в общем случае не является оптимальным фильтром. Кроме того, при плохой оценке начального состояния (сильно отличающейся от истинного, заранее не известного начального состояния) МФК может быстро расходиться из-за ошибок, обусловленных линеаризацией нелинейных функций и .
Еще одной проблемой, возникающей при использовании МФК, является то, что ковариационная матрица ошибок оценки , вычисляемая с помощью соотношения (3.51), оказывается переоцененной, т. е. дисперсии ошибок оценки оказываются слишком малыми по сравнению с их истинными, но не известными, значениями. Для исправления этого недостатка при решении практических задач вводят так называемый стабилизирующий шум, т.е. искусственно увеличивают ковариационную матрицу случайного воздействия .
Чтобы уменьшить влияние указанных недостатков в последние годы появился новый вариант ФК, который получил название нецентрированный фильтр Калмана (НФК), который является более точным и более робастным по сравнению с МФК. Тем не менее, МФК применяется достаточно широко.