
- •Московский авиационный институт (национальный исследовательский университет)
- •Кафедра № 604 тексты лекций
- •Содержание аздел 3. Методы апостериорного статистического анализа систем
- •Тема 3.1. Состав су ла. Задачи навигации и наведения. Принцип разделения
- •Тема 3.2. Общая постановка задачи оценивания состояния динамической системы
- •Тема 3.3. Оценивание состояния линейной динамической системы по полной выборке
- •Тема 3.4. Оценивание состояния нелинейной динамической системы по полной выборке
- •Тема 3.5. Оценивание состояния линейной динамической системы по полной выборке методом взвешенных наименьших квадратов
- •Тема 3.6. Рекуррентное оценивание состояния линейной динамической системы (фильтр Калмана)
- •Тема 3.7. Особенности процесса рекуррентного оценивания состояния линейной динамической системы с помощью фильтра Калмана
- •Тема 3.8. Модифицированный фильтр Калмана
- •Тема 3.9. Состав и структура имитационной модели процесса оценивания состояния динамической системы с помощью фильтра Калмана и его модификаций
Тема 3.7. Особенности процесса рекуррентного оценивания состояния линейной динамической системы с помощью фильтра Калмана
Анализируя соотношения прогноза и пересчета оценок и их ковариационных матриц с помощью фильтра Калмана, можно выделить следующие особенности этих соотношений.
1.
Ковариационные матрицы
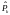 и
и
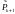 можно рассчитывать заранее
до поступления измерений
,
т.к. в формулы (3.42) и (3.44) для прогноза и
пересчета ковариационных матриц сами
измерения не
входят.
можно рассчитывать заранее
до поступления измерений
,
т.к. в формулы (3.42) и (3.44) для прогноза и
пересчета ковариационных матриц сами
измерения не
входят.
Рассчитав
изменение ковариационных матриц
и
на шагах по времени, можно вычислить
среднеквадратические отклонения
априорных и апостериорных оценок
отдельных переменных вектора состояния
 и
и
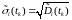 ,
,
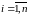 .
Используя эти данные, можно построить
трубки
.
Используя эти данные, можно построить
трубки
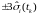 и
и
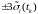 ,
характеризующие диапазоны возможных
значений ошибок оценки соответствующей
координаты
,
характеризующие диапазоны возможных
значений ошибок оценки соответствующей
координаты
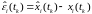 ,
и
,
и
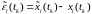 в которые могут попасть эти ошибки с
вероятностью 0.997 перед (
)
и после (
обработки очередного измерения.
в которые могут попасть эти ошибки с
вероятностью 0.997 перед (
)
и после (
обработки очередного измерения.
Типовой
график изменения трубок
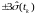 и
и
 для одной из координат вектора состояния
приведен на рис. 3.4. При пересчете оценки
в моменты поступления измерений с.к.о.
ошибок оценки, как правило, уменьшаются,
т.е.
для одной из координат вектора состояния
приведен на рис. 3.4. При пересчете оценки
в моменты поступления измерений с.к.о.
ошибок оценки, как правило, уменьшаются,
т.е.
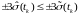 ,
так как измерения несут в себе информацию,
позволяющую уточнить
состояние системы. Наоборот, при прогнозе
оценки на интервалах между моментами
и
с.к.о. ошибок оценки, как правило,
возрастают, т.е.
,
так как измерения несут в себе информацию,
позволяющую уточнить
состояние системы. Наоборот, при прогнозе
оценки на интервалах между моментами
и
с.к.о. ошибок оценки, как правило,
возрастают, т.е.
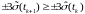 ,
так как на систему действуют случайные
возмущения
,
так как на систему действуют случайные
возмущения
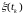 ,
увеличивающие
неопределенность
знания состояния системы.
,
увеличивающие
неопределенность
знания состояния системы.

Рис. 3.4. Трубки ошибок оценки состояния системы с помощью фильтра Калмана
2. Если система, состояние которой оценивается с помощью фильтра Калмана, является стационарной и устойчивой, то в типовых графиках трубок ошибок оценки можно выделить два режима: переходный и стационарный (установившийся). В переходном режиме величины с.к.о. ошибок оценки уменьшаются, начиная с их начальных априорных значений. Это уменьшение происходит благодаря увеличению общего числа измерений, несущих в себе информацию о состоянии системы, которые используются для получения оценки состояния к текущему моменту времени.
Проведя заранее расчет изменений ковариационной матрицы и определив длительность переходного режима, можно установить интервал времени, в течение которого необходимо проводить и обрабатывать измерения в реальной системе, чтобы гарантировать требуемую точность получаемых оценок.
В
стационарном
режиме возникает своеобразный баланс
между уточнением
оценки (уменьшением ее с.к.о.) благодаря
обработке очередного поступившего
измерения
 и снижением точности оценки из-за
случайного воздействия
,
действующего на систему на шаге,
предшествовавшем моменту
.
и снижением точности оценки из-за
случайного воздействия
,
действующего на систему на шаге,
предшествовавшем моменту
.
3. Не следует думать, что процесс оценивания состояния динамической системы всегда сходится, т. е. с.к.о. и трубки ошибок оценки переменных состояния системы всегда уменьшаются. Существует ряд причин, из-за которых процесс оценивания состояния оказывается расходящимся, а если и сходится, то недопустимо медленно.
Рассмотрим основные из этих причин.
а)
Первым условием, которое должно
выполняться при разработке фильтра
Калмана, является, так называемое,
условие наблюдаемости
системы. На качественном
уровне это условие означает, что в состав
вектора измерений
должны входить такие компоненты, которые
не только должны быть доступны
измерениям
с помощью используемых приборов
(измерительных устройств), но также быть
чувствительны
к изменениям
переменных состояния системы. Если
переменные состояния системы, входящие
в вектор
 ,
изменяются во времени, но эти изменения
не
отражаются
в изменениях компонент вектора измерений
,
то система с таким набором измеряемых
параметров – ненаблюдаемая,
и некоторые переменные состояния системы
по таким измерениям оценить невозможно.
Ситуацию можно исправить, только изменив
состав
вектора измерений.
,
изменяются во времени, но эти изменения
не
отражаются
в изменениях компонент вектора измерений
,
то система с таким набором измеряемых
параметров – ненаблюдаемая,
и некоторые переменные состояния системы
по таким измерениям оценить невозможно.
Ситуацию можно исправить, только изменив
состав
вектора измерений.
В теории линейных динамических систем сформулированы определенные правила, которые позволяют проверить заранее наблюдаемость системы, располагая уравнениями динамики системы и уравнениями измерений.
Попутно отметим, что помимо свойства наблюдаемости, существуют еще два свойства линейных динамических систем: управляемость и идентифицируемость.
Свойство управляемости означает, что органы управления в системе должны быть такими, при которых обеспечивалась бы возможность изменения всех регулируемых переменных состояния системы. Например, имея возможность управлять тягой ЛА, направленной вдоль продольной оси ЛА, можно менять величину скорости движения ЛА, но невозможно управлять направлением движения ЛА. Для этого необходимо иметь дополнительные устройства, позволяющие изменять угловое положение ЛА в пространстве (например, аэродинамические рули), или использовать дополнительно двигатели поперечного управления.
Свойство
идентифицируемости
похоже на свойство наблюдаемости.
Наличие или отсутствие этого свойства
указывает на возможность или невозможность
оценки параметров (матриц
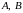 )
в уравнении состояния динамической
системы с помощью вектора измерений
.
)
в уравнении состояния динамической
системы с помощью вектора измерений
.
б) Второй причиной, из-за которой сформированный фильтр Калмана может оказаться расходящимся, может быть существенное расхождение между моделью движения системы, представленной ее переходной матрицей и используемой в соотношениях прогноза, и движением (динамикой) реальной системы, в которой проводятся измерения.
Математическая модель системы всегда приближенный аналог реальной системы. Допустимую степень их близости определяет исследователь. Чтобы вычисления в фильтре Калмана в реальном масштабе времени выполнялись быстро, желательно заложить в фильтр модель движения наблюдаемой системы как можно проще. В ряде случаев такое упрощение может стать причиной расходимости фильтра.
Более того, реальные системы, как правило, нелинейные, а фильтр Калмана – это алгоритм оценивания состояния линейной системы. Поэтому при создании фильтра приходится проводить линеаризацию уравнений движения рассматриваемой системы и уравнений измерений. Ошибки линеаризации также часто становятся причиной расходимости фильтра.
4. Даже если сходимость процесса оценивания с помощью фильтра Калмана обеспечивается, скорость сходимости и конечная точность оценок может быть различной. На эти характеристики, помимо указанных выше ошибок модели, влияют:
а) Величина шага между измерениями, т.е. частота проводимых измерений. Эта частота зависит от технических характеристик используемых измерительных приборов.
б) Точность проводимых измерений, также зависящая от технических характеристик используемых приборов и характеризуемая ковариационной матрицей .
в) Характеристики случайных возмущений , действующих на систему в полете, определяемые ковариационной матрицей .
г)
Величина и точность знания априорных
оценок состояния системы, характеризуемых
вектором
и матрицей
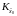 .
.
С учетом всего изложенного выше можно сделать вывод о том, что создание эффективно работающего фильтра Калмана - это не тривиальная процедура, результат которой зависит от квалификации и опыта разработчика, доступных измерительных и вычислительных средств, а также, в какой-то степени, и от удачи.
