
- •Московский авиационный институт (национальный исследовательский университет)
- •Кафедра № 604 тексты лекций
- •Содержание аздел 3. Методы апостериорного статистического анализа систем
- •Тема 3.1. Состав су ла. Задачи навигации и наведения. Принцип разделения
- •Тема 3.2. Общая постановка задачи оценивания состояния динамической системы
- •Тема 3.3. Оценивание состояния линейной динамической системы по полной выборке
- •Тема 3.4. Оценивание состояния нелинейной динамической системы по полной выборке
- •Тема 3.5. Оценивание состояния линейной динамической системы по полной выборке методом взвешенных наименьших квадратов
- •Тема 3.6. Рекуррентное оценивание состояния линейной динамической системы (фильтр Калмана)
- •Тема 3.7. Особенности процесса рекуррентного оценивания состояния линейной динамической системы с помощью фильтра Калмана
- •Тема 3.8. Модифицированный фильтр Калмана
- •Тема 3.9. Состав и структура имитационной модели процесса оценивания состояния динамической системы с помощью фильтра Калмана и его модификаций
Тема 3.6. Рекуррентное оценивание состояния линейной динамической системы (фильтр Калмана)
Рассмотренный в предыдущей теме алгоритм оценивания состояния линейной динамической системы по полной выборке методом взвешенных наименьших квадратов обладает рядом недостатков:
Алгоритм громоздок, так как при проведении расчетов с помощью соотношений (3.34) – (3.35) или (3.36) требуется выполнять матричные операции с векторами и матрицами большой размерности.
Алгоритм позволяет оценивать начальное состояние системы без учета детерминированных и случайных возмущений, действующих на систему в ходе ее движения.
Алгоритм позволяет получить оценку состояния системы только после получения результатов всех измерений, а не по мере их получения (хотя этот недостаток может быть устранен путем применения алгоритма к выборке нарастающего объема).
Поэтому на практике в настоящее время широкое распространение получил рекуррентный вариант этого алгоритма, впервые предложенный американским ученым Рудольфом Е. Калманом в 1960 году и получивший название фильтр Калмана.
Целью данной темы является вывод соотношений фильтра Калмана. В настоящее время существует несколько подходов к выводу этих соотношений. Здесь будут использован подход, основанный на использовании соотношений (3.34) – (3.35), образующих алгоритм оценивания по полной выборке измерений.
Постановка задачи. Рассматривается линейная динамическая система, изменение состояния которой описывается рекуррентным соотношением:
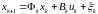 . (3.37)
. (3.37)
В этом соотношении:
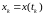 - вектор состояния системы
размерности
в дискретный момент времени
- вектор состояния системы
размерности
в дискретный момент времени
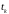 ;
;
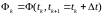 -
переходная матрица системы размерности
,
связывающая состояния системы в моменты
-
переходная матрица системы размерности
,
связывающая состояния системы в моменты
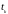 и
и
 ;
;
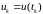 - вектор регулярных
(неслучайных) воздействий на систему
размерности
- вектор регулярных
(неслучайных) воздействий на систему
размерности
 в момент
;
в момент
;
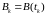 - матрица размерности
- матрица размерности
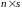 ,
описывающая влияние компонент вектора
,
описывающая влияние компонент вектора
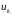 на переменные состояния, входящие в
вектор
на переменные состояния, входящие в
вектор
 ,
в момент
;
,
в момент
;
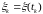 - дискретный векторный
белый шум, состоящий из
компонент – гауссовская (нормально
распределенная) абсолютно случайная
последовательность, состояния которой
в разные моменты времени статистически
независимы друг от друга. В каждый момент
времени
вектор
- дискретный векторный
белый шум, состоящий из
компонент – гауссовская (нормально
распределенная) абсолютно случайная
последовательность, состояния которой
в разные моменты времени статистически
независимы друг от друга. В каждый момент
времени
вектор
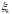 характеризуется нулевым вектором
математических ожиданий
характеризуется нулевым вектором
математических ожиданий
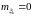 и заданной ковариационной матрицей
и заданной ковариационной матрицей
 ,
т.е.
,
т.е.
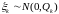 ,
где символ
обозначает нормально распределенную
векторную случайную величину.
,
где символ
обозначает нормально распределенную
векторную случайную величину.
Система,
описываемая соотношением (3.37), начинает
движение из случайного состояния
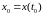 .
До начала проведения и обработки
измерений известна априорная
оценка начального
состояния
.
До начала проведения и обработки
измерений известна априорная
оценка начального
состояния
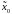 и ковариационная
матрица этой оценки
и ковариационная
матрица этой оценки
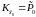 ,
т.е.
,
т.е.
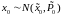 .
.
В
моменты
 в системе проводятся измерения
в системе проводятся измерения
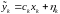 (3.38)
(3.38)
где:
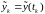 - вектор измерений
размерности
;
- вектор измерений
размерности
;
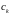 - матрица измерений
размерности
- матрица измерений
размерности
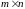 ;
;
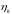 - дискретный векторный
белый шум, состоящий из
компонент – гауссовская (нормально
распределенная) абсолютно случайная
последовательность, состояния которой
в разные моменты времени статистически
независимы друг от друга. В каждый момент
времени
характеризуется вектором математических
ожиданий
- дискретный векторный
белый шум, состоящий из
компонент – гауссовская (нормально
распределенная) абсолютно случайная
последовательность, состояния которой
в разные моменты времени статистически
независимы друг от друга. В каждый момент
времени
характеризуется вектором математических
ожиданий
 и заданной ковариационной матрицей
и заданной ковариационной матрицей
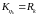 ,
т.е.
,
т.е.
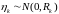 .
.
Требуется
составить рекуррентный алгоритм
обработки измерений
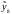 ,
,
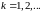 по мере их поступления, обеспечивающий
получение оценок состояния системы
,
оптимальных по критерию наименьших
квадратов. При этом характеристики
системы и измерений, характеризуемые
матрицами
по мере их поступления, обеспечивающий
получение оценок состояния системы
,
оптимальных по критерию наименьших
квадратов. При этом характеристики
системы и измерений, характеризуемые
матрицами
 ,
,
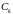 ,
,
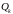 ,
,
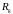 ,
а также начальная априорная оценка
и ее ковариационная матрица
,
а также начальная априорная оценка
и ее ковариационная матрица
 считаются известными (заданными).
считаются известными (заданными).
Соотношения пересчета оценок. Для решения задачи воспользуемся соотношениями (3.34) – (3.35), полученными выше для оценки состояния по полной выборке измерений. Вначале перепишем эти соотношения с учетом введенных новых (более компактных) обозначений:
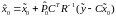 , (3.39)
, (3.39)
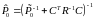 . (3.40)
. (3.40)
Теперь
предположим, что обрабатывается не все
измерения, полученные в моменты времени
 и вошедшие в совокупный вектор
,
а измерения, полученные в один
момент времени
,
т.е.
и вошедшие в совокупный вектор
,
а измерения, полученные в один
момент времени
,
т.е.
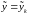 .
При этом размерность вектора
равна
,
т.е. числу параметров, измеряемых
одновременно. Кроме того, будем
предполагать, что априорная оценка
.
При этом размерность вектора
равна
,
т.е. числу параметров, измеряемых
одновременно. Кроме того, будем
предполагать, что априорная оценка
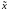 задана не в момент
,
а в момент
,
т.е. непосредственно
перед измерением, которое проводится
в момент
.
задана не в момент
,
а в момент
,
т.е. непосредственно
перед измерением, которое проводится
в момент
.
В
этом случае совокупная матрица измерений
трансформируется в матрицу
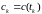 ,
матрица
,
матрица
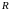 - в
- в
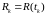 ,
а (3.39) и (3.40) становятся следующими:
,
а (3.39) и (3.40) становятся следующими:
 , (3.41)
, (3.41)
 . (3.42)
. (3.42)
В этих соотношениях:
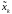 - это априорная
оценка вектора состояния по отношению
к измерению
;
- это априорная
оценка вектора состояния по отношению
к измерению
;
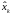 - это апостериорная
оценка вектора состояния, полученная
с учетом измерения
;
- это апостериорная
оценка вектора состояния, полученная
с учетом измерения
;
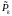 - это ковариационная матрица оценки
вектора состояния, априорной
по отношению к измерению
;
- это ковариационная матрица оценки
вектора состояния, априорной
по отношению к измерению
;
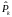 - ковариационная матрица апостериорной
оценки, полученной с учетом измерения
.
- ковариационная матрица апостериорной
оценки, полученной с учетом измерения
.
По аналогии с (3.36) соотношение (3.42) также можно переписать в другой форме:
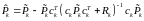 . (3.42')
. (3.42')
Вводя обозначение:
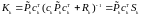 ,
называемый коэффициентом (матрицей)
Калмана, где
,
называемый коэффициентом (матрицей)
Калмана, где
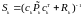 ,
(3.41) и (3.42) можно переписать так:
,
(3.41) и (3.42) можно переписать так:
 (3.41’')
(3.41’')
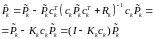 .
(3.42’')
.
(3.42’')
Таким образом, с помощью (3.41) – (3.42) на каждом шаге измерений происходит пересчет априорных характеристик и в апостериорные характеристики и . Поэтому соотношения (3.41) – (3.42) называют соотношениями пересчета фильтра Калмана.
Обратим внимание на важные особенности формул, входящих в соотношения пересчета:
для пересчета оценки состояния с помощью (3.41) вначале с помощью формулы
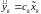 на основе априорных данных (по отношению
к измерению
)
определяется, каким должно быть измерение
в этот момент;
на основе априорных данных (по отношению
к измерению
)
определяется, каким должно быть измерение
в этот момент;затем вычисляется разность
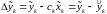 между фактическим измерением
и его предполагаемым значением
;
между фактическим измерением
и его предполагаемым значением
;далее эта разность с помощью матрицы Калмана
 пересчитывается в поправку к оценке
вектора состояния
пересчитывается в поправку к оценке
вектора состояния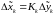 .
Матрица Калмана учитывает интегрально
степень доверия
к проведенному измерению (его вес),
в том числе ковариационную матрицу
.
Матрица Калмана учитывает интегрально
степень доверия
к проведенному измерению (его вес),
в том числе ковариационную матрицу
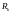 ошибок текущего измерения;
ошибок текущего измерения;наконец, полученная поправка добавляется к априорной оценке , образуя новую (уже апостериорную) оценку .
Соотношения
прогноза оценок.
Чтобы применить соотношения пересчета
(3.41) – (3.42), необходимо знать априорные
оценки
и
.
Для расчета этих оценок в фильтре Калмана
используются соотношения
прогноза. Эти
соотношения устанавливают связь между
апостериорными оценками
и
,
полученными после
обработки текущего измерения
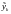 с помощью соотношений пересчета (3.41) –
(3.42), с априорными оценками
с помощью соотношений пересчета (3.41) –
(3.42), с априорными оценками
 и
и
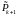 перед следующим
измерением.
перед следующим
измерением.
В динамической системе, движение которой описывается с помощью модели с дискретным временем, соотношения прогноза нетрудно получить с помощью уравнения движения системы (3.37).
Действительно,
применяя операцию усреднения к левой
и правой частям соотношения (3.37),
записанного для моментов времени
и
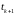
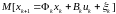 ,
,
получаем:
 (3.43)
(3.43)
так
как
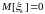 ,
,
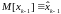 ,
а
,
а
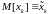 (напомним: термины математическое
ожидание и оценка
в данном случае являются синонимами).
(напомним: термины математическое
ожидание и оценка
в данном случае являются синонимами).
Чтобы спрогнозировать ковариационную матрицу, вычтем (3.43) из (3.37). Получим соотношение в отклонениях:
 ,
,
где: 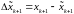 ;
;
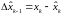 .
.
Отсюда находим:
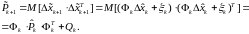 . (3.44)
. (3.44)
Таким образом, оценку состояния системы и ковариационную матрицу этой оценки между измерениями прогнозируем с помощью соотношений прогноза, образующих вторую часть фильтра Калмана:
, (3.43’)
 . (3.44’)
. (3.44’)
Соотношения
прогноза (3.43) – (3.44) и пересчета (3.41) –
(3.42) используются поочередно.
Если первое
измерение
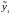 поступает в момент
поступает в момент
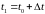 ,
а начальная априорная оценка состояния
и ее ковариационная матрица
заданы для момента
,
то вначале
используются именно соотношения
прогноза, чтобы
получить априорные оценки
,
а начальная априорная оценка состояния
и ее ковариационная матрица
заданы для момента
,
то вначале
используются именно соотношения
прогноза, чтобы
получить априорные оценки
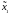 и
и
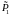 перед
этим первым измерением.
перед
этим первым измерением.
Чтобы использовать (3.43)
– (3.44) применительно к начальным
и
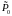 в унифицированном
виде, целесообразно переименовать
эти характеристики в
в унифицированном
виде, целесообразно переименовать
эти характеристики в
 и
и
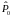 ,
т.е. рассматривать их как оценки,
апостериорные
по отношению к предшествующему
этапу функционирования
системы, на котором эти характеристики
были как-то получены.
,
т.е. рассматривать их как оценки,
апостериорные
по отношению к предшествующему
этапу функционирования
системы, на котором эти характеристики
были как-то получены.
Конкретный пример оценивания состояния динамической системы с помощью фильтра Калмана рассматривается на практическом занятии по теме.
