Тема 3.5. Оценивание состояния линейной динамической системы по полной выборке методом взвешенных наименьших квадратов

В данной теме вернемся к задаче оценивания состояния линейной динамической системы по полной выборке методом наименьших квадратов.

При решении этой задачи можно учесть априорную информацию, которой обладает исследователь. Такой информацией является:

• априорная оценка начального состояния системы 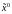, известная до проведения измерений 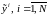в реальной системе, а также априорная ковариационная матрица 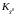, характеризующая точность знания этой априорной оценки;

• ковариационная матрица случайных ошибок измерений .

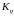При некоррелированных ошибках измерений матрица является диагональной. Диагональными элементами этой матрицы являются дисперсии ошибок измерений соответствующих компонент вектора измерений.

С учетом указанной априорной информации введенный ранее критерий наименьших квадратов (3.11)

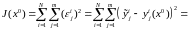(3.30)

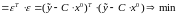
можно модифицировать (улучшить), заменив его новым критерием вида:

. (3.31)

Первое слагаемое в этом модифицированном критерии есть взвешенная сумма квадратов отклонений компонент искомой оценки начального вектора состояния от соответствующих компонент априорной оценки . Эти квадраты входят в сумму с весами, обратно пропорциональными соответствующим диагональным элементам (дисперсиям) ковариационной матрицы 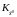, характеризующим точность априорного знания априорных оценок компонент начального вектора состояния . Чем меньше дисперсия априорной оценки 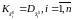, с тем большим весом, равным , входит соответствующее слагаемое в общую сумму, и наоборот.

Элементы второго слагаемого, равные квадратам отклонений оценок компонент вектора измерений от соответствующих компонент вектора фактических измерений, также взвешены с весами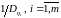 , характеризующими значимость (вес) каждого измерения в общей сумме. Такими весами являются величины, обратные дисперсии ошибок соответствующего измерения. Чем меньше дисперсия ошибок измерения, тем более точным является это измерение, и тем больший вес можно придать этому измерению, и наоборот.

Решение задачи оптимизации оценки с использованием критерия (3.31)

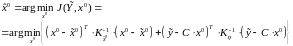(3.32)

получило название «оценка состояния системы по полной выборке методом взвешенных наименьших квадратов».

Модифицированный критерий наименьших квадратов приводит к получению более точного решения задачи оценивания по сравнению со стандартным методом наименьших квадратов. Естественно, этот критерий может быть применен лишь в том случае, когда известны априорные оценки переменных состояния и дисперсии этих оценок, а также дисперсии ошибок проводимых измерений.

Конкретный способ решения задачи оптимизации (3.31) существенно зависит от того, какой является зависимость вектора измерений от вектора состояния : линейной или нелинейной.

При линейной зависимости задача оптимизации имеет аналитическое решение, получаемое с использованием необходимых условий минимума функции. При нелинейном уравнении измерений задачу поиска оптимальной оценки состояния системы приходится решать численно с использованием какого-либо метода математического программирования.

В линейном случае, используя необходимое условие минимума функции и учитывая рассмотренное выше правило дифференцирования квадратичной формы по вектору, получаем:

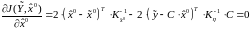. (3.33)

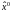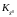Для решения этого матричного уравнения относительно сократим оба слагаемых на 2 и применим операцию транспонирования. Помня, что ковариационные матрицы и 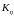- это симметричные матрицы и обратные к ним матрицы – тоже симметричные, а поэтому их транспонирование дает те же матрицы, получаем:

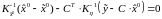
Выделяя член с , имеем:

.

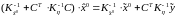В правой части добавим и вычтем 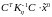. Получим:

.

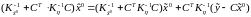Умножение слева обеих частей этого выражения на 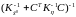дает искомое соотношение:

, (3.34)

где:

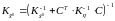. (3.35)

Можно доказать [ ], что матрица 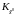, определяемая выражением (3.35), является именно ковариационной матрицей апостериорной оценки начального вектора состояния, рассчитанной с учетом априорной оценки этого состояния и всех измерений, входящих в вектор .

Также можно доказать, что вместо (3.35) для расчета можно воспользоваться эквивалентной формулой:

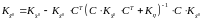. (3.36)

Преимущество этой формулы заключается в том, что при ее использовании отпадает необходимость в двойном обращении матриц и .

Возможность замены (3.35) на (3.36) получила название "лемма об обращении матриц".

Конкретный пример решения задачи с помощью приведенных соотношений будет рассмотрен на практическом занятии.