
- •Московский авиационный институт (национальный исследовательский университет)
- •Кафедра № 604 тексты лекций
- •Содержание аздел 3. Методы апостериорного статистического анализа систем
- •Тема 3.1. Состав су ла. Задачи навигации и наведения. Принцип разделения
- •Тема 3.2. Общая постановка задачи оценивания состояния динамической системы
- •Тема 3.3. Оценивание состояния линейной динамической системы по полной выборке
- •Тема 3.4. Оценивание состояния нелинейной динамической системы по полной выборке
- •Тема 3.5. Оценивание состояния линейной динамической системы по полной выборке методом взвешенных наименьших квадратов
- •Тема 3.6. Рекуррентное оценивание состояния линейной динамической системы (фильтр Калмана)
- •Тема 3.7. Особенности процесса рекуррентного оценивания состояния линейной динамической системы с помощью фильтра Калмана
- •Тема 3.8. Модифицированный фильтр Калмана
- •Тема 3.9. Состав и структура имитационной модели процесса оценивания состояния динамической системы с помощью фильтра Калмана и его модификаций
Тема 3.4. Оценивание состояния нелинейной динамической системы по полной выборке
В математической модели нелинейной динамической системы с дискретным временем изменение по времени состояния системы описывается рекуррентным соотношением вида:
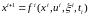 . (3.19)
. (3.19)
В этом соотношении:
 - нелинейная вектор-функция размерности
- нелинейная вектор-функция размерности
 ;
;
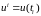 - векторная последовательность регулярных
(неслучайных) воздействий на систему
размерности
- векторная последовательность регулярных
(неслучайных) воздействий на систему
размерности
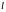 ;
;
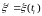 -
векторная дискретная случайная
последовательность размерности
-
векторная дискретная случайная
последовательность размерности
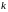 ,
описывающая случайные воздействия на
систему.
,
описывающая случайные воздействия на
систему.
Вектор измерений в нелинейной системе связан с состоянием системы нелинейным соотношением:
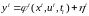 , (3.20)
, (3.20)
где
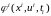 - нелинейная вектор функция, число
компонент
равно числу компонент вектора измерений
;
- нелинейная вектор функция, число
компонент
равно числу компонент вектора измерений
;
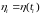 - векторный дискретный белый шум
размерности
,
описывающий случайные ошибки измерений.
- векторный дискретный белый шум
размерности
,
описывающий случайные ошибки измерений.
Также возможен смешанный вариант задачи оценивания в нелинейной системе, в котором только одно из двух уравнений (3.19) или (3.20) является нелинейным, а второе остается линейным. Например, движение системы описывается линейным уравнением с помощью переходной матрицы вида (3.1) или (3.7), а измерения нелинейно зависят от состояния .
В
примере
в варианте
измерений 2 переменные состояния объекта
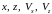 и измерения
и измерения
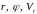 в каждый момент проведения измерений
связаны друг с другом следующими
нелинейными
соотношениями (см.
рис. 3.2):
в каждый момент проведения измерений
связаны друг с другом следующими
нелинейными
соотношениями (см.
рис. 3.2):

дальность до объекта; (3.21)
дальность до объекта; (3.21)
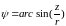 угол азимута
объекта; (3.22)
угол азимута
объекта; (3.22)
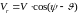
доплеровская скорость; (3.23)
доплеровская скорость; (3.23)
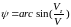
угол визирования объекта;
угол визирования объекта;
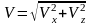
скорость объекта.
скорость объекта.
Рассматривая уравнения (3.21), (3.22) и (3.23) совместно, получаем векторное нелинейное уравнение измерений:
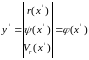 . (3.24)
. (3.24)
Выведем
соотношения для расчета состояния
нелинейной
системы, движение которой описывается
соотношением (3.19), по полной выборке
измерений в частном случае, когда
регулярные воздействия
 и случайные воздействия
и случайные воздействия
 отсутствуют.
отсутствуют.
Для решения задачи необходимо, как и в линейном случае, выразить все состояния системы и все измерения через начальное состояние.
При нелинейных уравнениях измерений имеем:
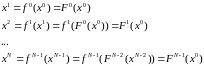 . (3.25)
. (3.25)
Уравнения измерений (3.20) также можно выразить через начальное состояние системы:
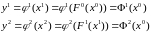 .
(3.26)
.
(3.26)
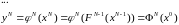
Все эти уравнения можно записать в виде единого векторного нелинейного уравнения измерений:
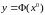 , (3.27)
, (3.27)
где
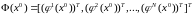 - нелинейная вектор-функция всех
измерений, где
-
число параметров, измеряемых при каждом
отдельном измерении.
- нелинейная вектор-функция всех
измерений, где
-
число параметров, измеряемых при каждом
отдельном измерении.
Вектор
фактических
измерений
отличается от
присутствием вектора ошибок измерений
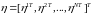 той же размерности
.
той же размерности
.
Как и в линейном случае, разность между векторами и есть вектор ошибок оценки:
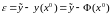 . (3.28)
. (3.28)
Значения компонент вектора зависят от случайных ошибок, содержащихся в проведенных измерениях, а также от значений компонент начального вектора состояния , которые заранее не известны и которые требуется оценить с помощью проведенных измерений.
Критерий наименьших квадратов как скалярная характеристика ошибок оценки начального состояния записывается так:
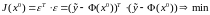 . (3.29)
. (3.29)
Однако
в данной ситуации (в отличие от линейного
случая) решить задачу минимизации
критерия
 аналитически не удается в силу нелинейной
зависимости
аналитически не удается в силу нелинейной
зависимости
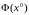 .
Эту задачу можно решить численно,
используя один из поисковых
методов оптимизации. Блок-схема решения
задачи поиска оптимальной оценки
начального состояния
приведена на рис. 3.3.
.
Эту задачу можно решить численно,
используя один из поисковых
методов оптимизации. Блок-схема решения
задачи поиска оптимальной оценки
начального состояния
приведена на рис. 3.3.
Оценки состояния системы в последующие моменты времени могут быть вычислены по найденной оценке с помощью соотношений (3.25). Численный пример решения задачи оценивания состояния нелинейной системы по полной выборке измерений будет рассмотрен на практическом занятии по данной теме.
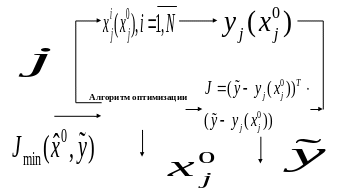
Рис. 3.3. Блок-схема алгоритма оценивания состояния нелинейной системы по полной выборке измерений
