Тема 3.3. Оценивание состояния линейной динамической системы по полной выборке

Математическая формулировка задачи. Для решения задачи оценивания состояния динамической системы требуется, прежде всего, располагать моделью движения (динамики) объекта (системы) и уравнениями измерений.

Как это обсуждалось ранее, модель динамики объекта описывает изменение состояния объекта в зависимости от начальных условий и внешних воздействий.

Уравнения измерений устанавливают связь между вектором состояния и вектором измерений в моменты проведения измерений.

Модель динамики объекта. В общем случае модель динамики объекта может быть линейной или нелинейной, с непрерывным или с дискретным временем.

Как это уже неоднократно обсуждалось ранее при решении задач априорного статического анализа, линейная модель движения объекта с непрерывным временем описывается векторным уравнением состояния в нормальной форме Коши:

, (3.1)

а вектор измерений 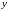связан с вектором состояния линейным алгебраическим соотношением

, (3.2)

где - вектор входов, действующих на систему (управляющих и возмущающих воздействий).

Движение объекта начинается из начального состояния .

Пример. В рассматриваемом примере движение объекта происходит непрерывно во времени и описывается следующей системой линейных дифференциальных уравнений:

. (3.1а)

при начальных условиях:

.

Уравнение (3.1а) можно переписать в векторной форме:

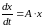, (3.1б)

где 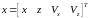- вектор состояния объекта;

- динамическая матрица объекта.

Если измерения проводятся в дискретные моменты времени 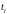с шагом , то для решения задачи оценивания необходимо перейти от модели динамики объекта в виде уравнений (3.1) с непрерывным временем к модели с дискретным временем, используя для этого переходную матрицу системы , связывающую состояния системы в моменты и .

Для получения переходной матрицы на интервале составляем однородное уравнение, соответствующее уравнению состояния (3.1):

, (3.3)

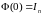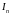и интегрируем его на интервале при начальном условии , где - единичная матрица размерности .

В примере 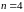. Учитывая вид динамической матрицы 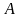, и полагая шаг малым, в примере можно записать:

(3.4)

Как видим, так как система (3.1а) – стационарная, то переходная матрица этой системы при фиксированном шаге является постоянной, не меняющейся во времени.

Зная переходную матрицу 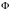, можно записать рекуррентное алгебраическое соотношение, связывающее состояния объекта в последовательные дискретные моменты времени, начиная с момента :

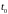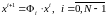. (3.5)

Здесь и ниже верхний индекс обозначает номер момента времени, в который рассматривается состояние системы и проводится измерение.

В примере соотношение (3.5) с учетом (3.4) есть искомая модель динамики объекта с дискретным временем, описывающая свободное движение объекта.

Уравнения измерений. При линейных уравнениях измерений вектор измерений без учета ошибок измерений выражается линейно через компоненты вектора состояния :

, . (3.6)

В примере в варианте 1 измерений вектор измерений 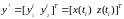, где:

- матрица измерений.

Здесь и в дальнейшем верхний индекс обозначает операцию транспонирования.

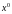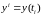Векторное уравнение измерений. Чтобы получить оценку состояния по полной выборке измерений , все измерения необходимо выразить через начальное состояние и объединить в единый вектор измерений. Согласно (3.6) векторы измерений зависят от векторов состояния . Последние, в свою очередь, с помощью переходной матрицы 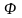можно выразить через начальное состояние :

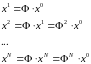. (3.7)

Используя эти соотношения, все векторы измерений также можно выразить через начальное состояние .

С учетом (3.6) имеем:

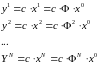. (3.8)

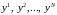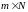Объединив векторы в единый вектор, получим вектор общей размерности , где - размерность вектора измерений в каждый момент проведения измерений, а 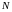- число моментов времени , когда проводились измерения.

Используя этот вектор, можно записать векторное уравнение измерений, связывающее объединенный вектор измерений с вектором :

, (3.9)

где - общая матрица измерений, имеющая размерность . Эта матрица с учетом (3.8) имеет следующую структуру:

.

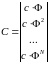Вектор проведенных измерений. Фактические измерения , полученные при наблюдениях за реальным объектом, отличаются от векторов присутствием в их составе случайных ошибок измерений , т.е.

, .

Векторы 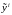также можно объединить в единый вектор проведенных измерений 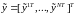. Этот вектор с учетом (3.9) можно представить в виде:

,

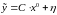Здесь  вектор случайных ошибок всех проведенных измерений, имеющий размерность .

Вектор ошибок оценки. Разность между вектором проведенных измерений 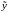и значением этого вектора , вычисленного при заданном векторе начальных условий - это вектор ошибок оценки:

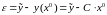. (3.10)

Размерность этого вектора равна размерности общего вектора измерений – . Значения компонент вектора зависят от случайных ошибок, содержащихся в проведенных измерениях, а также от значений компонент начального вектора состояния , которые заранее не известны и которые требуется оценить с помощью проведенных измерений.

Критерий оптимальности оценок. Напомним, что целью решения задачи оценивания является определение наиболее точной оценки истинного (неизвестного) начального состояния объекта . При этом, в соответствии с (3.10) каждому выбранному значению будет соответствовать определенный вектор ошибок оценки . Меняя , можно выбрать такое значение этого вектора, при котором вектор ошибок оценки будет наилучшим.

Вектор ошибок оценки нельзя сделать минимальным, поскольку любое значение , обеспечивающее уменьшение одних составляющих вектора ошибок, может привести к увеличению каких-либо других его компонент.

Поэтому для решения задачи оптимального выбора оценки начального состояния необходимо преобразовать вектор ошибок в некоторый эквивалентный скалярный критерий оптимальности оценки.

Критерий наименьших квадратов. Наиболее простым, удобным и поэтому наиболее широко распространенным критерием является критерий наименьших квадратов, предложенный впервые немецким ученым Гауссом. Этот критерий порождает метод оценивания, называемый методом наименьших квадратов.

При критерии наименьших квадратов в качестве скалярной характеристики ошибок оценки рассматривается сумма квадратов всех компонент вектора ошибок :

. (3.11)

В этой формуле:

- номер момента измерения ;

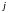- номер составляющей вектора измерений в этот момент.

В векторной записи этот критерий может быть переписан следующим образом:

. (3.11а)

При использовании данного критерия задача оптимального оценивания начального состояния объекта формулируется так:

определить такую оценку , при которой критерий достигает минимального значения, т.е.:

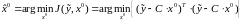. (3.12)

Решение задачи оценивания. Для вывода формулы, позволяющей определить вектор по методу наименьших квадратов, воспользуемся необходимым условием минимума:

.

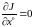Выражение для критерия в правой части (3.12) есть, так называемая, квадратичная форма. В теории матриц доказано, что производная квадратичной формы 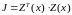по вектору вычисляется с помощью выражения:

.

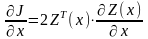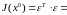
Применяя это общее правило к выражению 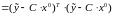, получаем:

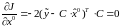(3.13)

Для решения этого уравнения относительно избавимся от -2 и применим операцию транспонирования к левой части (3.13). Вспоминая, что 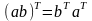, получим:

,

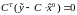или .

Умножая слева и справа на 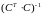, где верхний индекс обозначает обращение матрицы, и также вспоминая, что по определению , получаем окончательное выражение для искомой оценки начального вектора состояния:

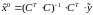. (3.14)

Найдя начальное состояние системы , можно вычислить оценки состояния системы во все последующие моменты времени, пользуясь формулами, аналогичными (3.7):

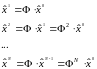. (3.15)

Ковариационная матрица ошибок оценки. Соотношение (3.14) может быть использовано и для получения ковариационной матрицы этой апостериорной оценки начального состояния.

По определению

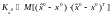, (3.16)

где:

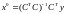- истинное (не известное) начальное состояние;

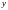- совокупный вектор измерений, соответствующий этому начальному состоянию.

Подстановка выражений для 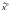и вида (3.14) в (3.16) дает:

.

Применяя правило транспонирования для произведения векторов или матриц, учитывая, что , а , а таже учитывая, что матрица 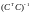- симметричная матрица (в силу симметричности квадратичной формы 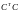) и поэтому 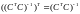), получаем:

. (3.17)

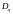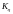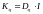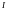В частном случае, когда дисперсии ошибок всех компонент вектора измерений во все моменты времени – одинаковые, равные , ковариационная матрица приобретает вид: , где - единичная матрица, размерность которой равна размерности совокупного вектора измерений, из (3.17) находим:

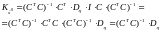(3.18)

При получении (3.18) учтено, что скалярная величина в матричном выражении может быть переставлена в любое место (в том числе в конец выражения), а произведение любой матрицы или вектора на единичную матрицу равно исходной матрице.

Соотношение (3.18) позволяет найти дисперсии и взаимные ковариационные моменты всех компонент вектора апостериорной оценки . Поэтому матрица получила название дисперсионная матрица.

Конкретный пример решения задачи оценивания состояния линейной системы по полной выборке применительно к исходным данным, указанным в начале данной темы, будет рассмотрен на практическом занятии.