1.2. Электрические цепи: элементы, схемы, законы, классификация

Основными элементами электрических цепей являются источники электромагнитной энергии (см. § 1.1), элементы передачи (линии электропередачи, линии связи) и преобразования (трансформаторы, различные преобразователи — выпрямители, инверторы и др.) энергии, а также приемники энергии, в которых электромагнитная энергия преобразуется в энергию других видов, например в механическую (электрические двигатели), химическую (аккумуляторы), тепловую (электрические печи) и т.п.

Источники энергии принято называть активными элементами, а ту часть цепи, в которой они действуют, — активной подцепью, все остальные элементы — пассивными элементами, а часть цепи, в которой нет активных элементов, — пассивной подцепью. Сложность изучения всего многообразия реальных элементов цепей (линий электропередачи, трансформаторов, генераторов и др.) породила необходимость выделения минимального набора простейших элементов, с помощью комбинаций которых можно описывать эти реальные элементы. К таким элементам относят источники энергии: источник ЭДС (схемное обозначение представлено на рис. 1.6, а), источник тока (рис. 1.6, б), резистор (рис. 1.6, в), конденсатор (рис. 1.6, г) и индуктивная катушка (рис. 1.6, д).

 

 

Для источника ЭДС (рис. 1.6, а) характерным является равенство напряжения между его выводами значению электродвижущей силы:

 

(1.1)

 

для источника тока (рис. 1.6, б) — численное равенство тока i элемента значению тока J источника:

 

(1.2)

 

для резистора (рис. 1.6, в) — линейная связь напряжения и тока:

 

(1.3)

 

для конденсатора (рис. 1.6, г) — линейная связь тока элемента с производной напряжения:

 

(1.4)

 

для катушки (рис. 1.6, д) — линейная связь напряжения с производной тока:

 

(1.5)

 

При этом уравнения (1.1)—(1.5) называют компонентными уравнениями рассматриваемых элементов, параметры R(G), С и L этих элементов — соответственно сопротивлением (проводимостью) резистора, емкостью конденсатора и индуктивностью катушки, а значения тока i(t), напряжения u(t) и ЭДС e(t) в момент времени t соответственно мгновенными значениями i, u, e.

Выражение (1.3) носит название закона Ома, а произведение мгновенных значений напряжения и тока p = ui, называемое мгновенной мощностью, для резистора равно р = ui = Ri² (закон Джоуля—Ленца). Мощность в данном случае определяет количество теплоты, выделяемое резистором в единицу времени. Таким образом, резистор (резистивный элемент) — это элемент, предназначенный для использования его электрического сопротивления. Единицей сопротивления является ом — 1 Ом = 1 В/1 А (проводимости — сименс — 1 См = 1 А/1 В), мгновенной мощности — ватт — 1 Вт = 1 В · 1 А.

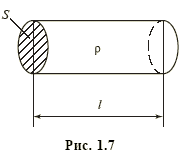
Сопротивлением R можно охарактеризовать любой проводник длиной l и сечением S (рис. 1.7), причем если ток распределен по сечению проводника равномерно, то , где ρ — удельное электрическое сопротивление, характеризующее свойства материала проводника. Единицей удельного электрического сопротивления является ом х метр (Ом · м). Поэтому в схеме замещения (см. ниже) электрической цепи резистивные элементы отражают не только собственно резисторы, но и сопротивления проводов линий электропередач, сопротивления проводников, из которых выполнены обмотки трансформаторов, электрических машин и т.п.

Конденсатор (емкостной элемент) запасает энергию электрического поля W_э = Cu²/2, его мгновенная мощность 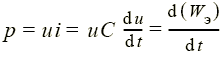— характеризует скорость изменения этой энергии во времени. Конденсатор выполняется в виде двух металлических пластин, разделенных слоем диэлектрика (рис. 1.8). Собственно емкость, для использования которой и предназначен этот элемент, представляет собой отношение двух равных по значению, но противоположных по знаку зарядов пластин, разнесенных в пространстве (рис. 1.8), к напряжению этого элемента С = q/u. Единицей емкости является фарад — 1 Ф = 1 Кл/1 В. Емкостью обладает не только конденсатор, но и пары проводов электропередач, емкостью характеризуется связь каждого из этих проводов с землей и т.д. При составлении схемы замещения реальной цепи необходимо отражать подобные связи емкостными элементами, входящими в схему наравне с конденсаторами.

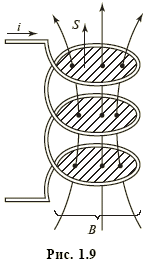
Катушка индуктивности (индуктивный элемент) запасает энергию магнитного поля W_м = Li²/2, ее мгновенная мощность характеризует скорость изменения этой энергии во времени. Конструктивно такой элемент часто выполняется из проводника в виде спирали (рис. 1.9).

Ток i в этом случае создает магнитное поле, направление индукции В которого показано линиями со стрелками. Интегрально его можно охарактеризовать для каждого витка потоком через поверхность S. Произведение этого потока на число витков w катушки называют потокосцеплением ψ = Фw. Индуктивность характеризует связь между этим потокосцеплением и вызывающим его током ψ = Li. Единицей магнитного потока является тесла — 1 Тл = 1 Вб · 1 м², индуктивности — генри — 1 Гн = 1 Тл/1 А. Таким образом, индуктивная катушка — это элемент цепи, предназначенный для использования его индуктивности. Индуктивностью помимо собственно катушек обладают и другие элементы реальных электрических цепей, в частности провода линий электропередач, что необходимо отражать в схемах замещения соответствующих цепей.

Таким образом, любая часть реальной электрической цепи обладает всеми перечисленными параметрами — R, L, С, а названные выше — резистор, конденсатор, катушка — суть элементы, в которых соответственно сопротивление, емкость и индуктивность являются основными параметрами, другими же параметрами обычно пренебрегают.

Электрическую цепь удобно изображать в виде чертежа, называемого схемой электрической цепи. Такая схема составляется из условных обозначений элементов цепи (см. рис. 1.6) и показывает их соединение. При этом последовательность элементов, имеющих один и тот же ток, называют ветвью, место соединения ветвей — узлом, замкнутый путь, проходящий по нескольким элементам, называют контуром. Для любого узла справедлив первый закон Кирхгофа: алгебраическая сумма мгновенных значений токов в ветвях, соединенных с данным узлом, равна нулю: ∑i = 0.

Для любого контура справедлив второй закон Кирхгофа: алгебраическая сумма напряжений на всех элементах любого замкнутого контура равна нулю: ∑u = 0.

Если число ветвей цепи равно В, узлов У, то число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно У – 1, по второму — В – У + 1 . Дополнив В уравнений, составленных по первому и второму законам Кирхгофа (У – 1 + В – У + 1 = В), компонентными уравнениями элементов цепи, можно получить полную систему ее уравнений, позволяющую решить задачу анализа: по заданной схеме и значениям параметров элементов рассчитать неизвестные токи и напряжения ветвей цепи.

Пример 1.1. Для цепи, изображенной на рис. 1.10, имеем: число узлов равно двум, число ветвей — трем, число элементов — четырем. Тогда согласно первому закону Кирхгофа имеем

 

(1.6)

 

согласно второму закону Кирхгофа:

 

(1.7)

 

Компонентные уравнения имеют вид

 

(1.8)

 

Полная система уравнений электрической цепи (1.6)—(1.8) позволяет по известным параметрам е = e(t), R, L, С найти все токи и напряжения активного (источник ЭДС) и трех пассивных (резистор, катушка индуктивности, конденсатор) элементов цепи, т.е. решить задачу анализа цепи при условии, что заданы также начальные значения (т.е. значения переменных в момент времени, равный нулю) тока катушки i₂(0) = i₀₂ и напряжения конденсатора u₃(0) = u₀₃, которые необходимы для решения алгебродифференциальных уравнений (1.6)—(1.8).

В общем случае для решения задачи анализа сложной электрической цепи (т.е. задачи определения всех неизвестных токов и напряжений ее элементов при известной схеме и параметрах — сопротивлениях, емкостях, индуктивностях, ЭДС и токах источников тока) полную систему уравнений составляют редко.

Более эффективными оказываются иные подходы, основанные, например, на различных преобразованиях схем (см. ниже) или использовании более простых — канонических уравнений, связывающих лишь часть из неизвестных переменных. Такие канонические уравнения оказывается возможным составлять относительно переменных, определяющих энергетическое состояние цепи, т.е. запасы ее электрической и магнитной энергии. Поэтому подобные канонические уравнения называют уравнениями состояния электрической цепи, а переменные, относительно которых они составляются, — переменными состояния. Из сказанного следует, что переменными состояния для электрических цепей являются токи индуктивных элементов, определяющих запас магнитной энергии, и напряжения емкостных элементов, определяющих запас электрической энергии.

Пример 1.2. Выразив ток i₃ из уравнения (1.6) i₃ = i₁ – i₂ и воспользовавшись компонентными уравнениями (1.8) u₁ = Ri₁, u = е, из системы уравнений (1.7) найдем

 

 

Следовательно,

Тогда из компонентных уравнений (1.8) 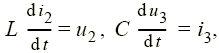уравнения u₂ = u₃ (1.7) и полученного уравнения для i₃ находим уравнения состояния электрической цепи, изображенной на рис. 1.10:

 

 

Полученная в примере 1.2 каноническая форма дифференциального уравнения удобна для аналитического либо численного (с помощью стандартных пакетов программ интегрирования дифференциальных уравнений) решения. Под решением здесь понимаются определенные зависимости тока индуктивного элемента i₂ = i₂(t) и напряжения емкостного элемента u₃(t) от времени. Располагая такими зависимостями и уравнениями (1.6), (1.8), аналогичные зависимости от времени для остальных переменных i₁(t), i₃(t), u₁(t), u₂(t) находят уже с помощью одних алгебраических операций.

Для электрической цепи закон сохранения энергии записывается в виде равенства суммы генерируемых источниками мгновенных мощностей сумме мгновенных мощностей остальных элементов Это выражение, представляющее собой запись теоремы Телледжена, показывает, что энергия источников расходуется на теплоту, выделяемую резисторами, и перераспределение запасов электрической и магнитной энергии, запасенных конденсаторами и катушками. В этой связи говорят о балансе мгновенных мощностей цепи.

Пример 1.3. Согласно теореме Телледжена для схемы рис. 1.10 имеем ei₁ = u₁i₁ + u₂i₂ + u₃i₃, где е = u.

Электрические цепи принято классифицировать по типу параметров элементов и типу электромагнитных процессов в них. Так, говорят о линейных цепях, если параметры элементов е = e(t), J = J(t), R, L, С не зависят от интенсивностей электромагнитных процессов (т.е. от токов и напряжений этих элементов). Подобные цепи описываются линейными системами уравнений, решение которых может быть достигнуто с использованием принципа суперпозиции (наложения), когда можно рассматривать вклад параметра е или J каждого источника энергии в решение независимо от вклада в него других источников. Линейные цепи называют стационарными, если параметры R, L, С их элементов — константы, и параметрическими, если эти параметры известные функции времени R = R(t), L = L(t), С = C(t). Если же параметры е, J, R, L, С зависят от интенсивности процессов, то сами элементы и цепи, их содержащие, называют нелинейными элементами и цепями. Уравнения таких цепей нелинейны, и поиск их решения с гарантированной точностью представляет собой весьма сложную задачу. Различают также элементы и цепи с сосредоточенными и распределенными параметрами. О сосредоточенных параметрах R, L, С говорят в том случае, когда они сосредоточены (локализованы) на определенном участке. Если же приходится учитывать геометрическую протяженность этого участка, то эти параметры считаются распределенными. Параметры R, L, С в этом случае характеризуют единицами Ом/м, Гн/м, Ф/м. Цепи с распределенными параметрами описываются уравнениями в частных производных, решение которых весьма трудоемко. Следует отметить, что допущение о линейности и сосредоточенности параметров справедливо лишь для определенных диапазонов интенсивностей процессов, т.е. является условным, и в этом смысле говорят о границах абстракций в теории электрических цепей. По типу электромагнитных процессов цепи подразделяют на цепи постоянных токов (если токи и напряжения всех элементов цепей не изменяются во времени), цепи переменных токов (если токи и напряжения всех элементов цепей изменяются во времени) и, в частности, цепи синусоидальных токов (если эти токи и напряжения цепей изменяются во времени по синусоидальным законам).

Следует заметить, что в частных случаях, когда процессы в цепях описываются функциями одного вида, например постоянными или синусоидальными функциями, расчет цепей резко упрощается. Существует масса приемов и методов расчета таких цепей. Ознакомимся с некоторыми из них. Но прежде всего обратим внимание на то, что в схемах замещения цепей постоянных токов отсутствуют емкостные и индуктивные элементы. В самом деле, из допущения о постоянстве тока из компонентного уравнения (1.5) индуктивного элемента (см. рис. 1.6, д) следует, что напряжение его будет равным нулю, т.е. сам индуктивный элемент в схеме замещения цепи на постоянном токе представляет собой идеальный проводник с нулевым сопротивлением — так называемую «закоротку». Из допущения о постоянстве напряжения для емкостного элемента (см. рис. 1.6, г) из компонентного уравнения (1.4) следует, что его ток в этом случае будет равен нулю, а сам емкостной элемент представляет собой «разрыв» ветви цепи. Полученная резистивная цепь описывается уже не дифференциальными, а чисто алгебраическими уравнениями, решение которых не представляет особой сложности.

Пример 1.4. Схема рис. 1.10 для случая, когда ЭДС источника e(t), токи i₁(t), i₂(t), i₃(t) и напряжения u₁(t), u₂(t), u₃(t) постоянны, т.е. е = Е, i₁ = I₁, i₂ = I₂, i₃ = I₃, u₁ = U₁, u₂ = U₂, u₃ = U₃, может быть представлена в виде рис. 1.11. При этом I₃ = 0, U₂ = 0, а токи I₁ = I₂ и напряжение U₃ находятся из уравнений второго закона Кирхгофа U₁ + U₂ = Е, U₃ = U₂, где U₁ = I₁R. Окончательно имеем I₁ = I₂ = E/R.

При расчетах резистивных цепей можно пользоваться следующими преобразованиями, основанными на использовании компонентных уравнений и уравнений Кирхгофа:

последовательно соединенные резисторы с сопротивлениями R₁ и R₂ (рис. 1.12, а) можно заменить одним эквивалентным резистивным элементом с сопротивлением R_э = R₁ + R₂ (рис. 1.12, б), не изменив при этом общего тока I и на пряжения U ветви;

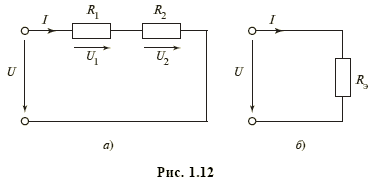
параллельно соединенные резисторы с проводимостями G₁ = l/R₁ и G₂ = l/R₂ (рис. 1.13, а) можно заменить одним эквивалентным резистивным элементом с проводимостью G_э = G₁ + G₂ (с сопротивлением (рис. 1.13, 6), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи;

источник ЭДС Е с внутренним сопротивлением R_вн (рис. 1.14, а) можно заменить источником тока J с внутренней проводимостью G_вн (рис. 1.14, б) при условии J = E/R_вн, G_вн = 1/R_вн; аналогично источник тока J с внутренней проводимостью G_вн (рис. 1.14, б) можно заменить источником ЭДС Е = J/G_вн с внутренним сопротивлением R_вн = 1/G_вн (рис. 1.14, а), не изменив при этом общего тока I и напряжения U рассматриваемого участка цепи.

Используя подобные методы преобразования схемы цепи, можно существенно упростить ее схему и соответственно расчет токов и напряжений. Наряду с подобными методами преобразования при расчете цепей постоянных токов или в более общем случае любых чисто резистивных цепей используют и специальные методы упрощения их схем. Наиболее известным из них является метод эквивалентного генератора.

Суть его сводится к эквивалентной замене любого активного (т.е. содержащего источники энергии) двухполюсника А (т.е. подцепи, присоединенной к остальной части цепи двумя узлами) (рис. 1.15, а) источником ЭДС Е_г, называемой ЭДС эквивалентного генератора с последовательно включенным внутренним сопротивлением R_г (рис. 1.15, 6). При этом значение Е_г равно напряжению так называемого «холостого хода», т.е. напряжению U на разомкнутых зажимах двухполюсника. Это напряжение можно непосредственно измерить, если цепь существует в виде реального устройства, или рассчитать, если она задана в виде схемы с известными параметрами. Внутреннее сопротивление такого генератора определяется как сопротивление двухполюсника А с замкнутыми источниками ЭДС и разорванными ветвями с источниками тока.

Пример 1.5. Определим параметры эквивалентного генератора активного двухполюсника (рис. 1.16, а). «Закоротив» источник ЭДС Е₁ и «разорвав» ветвь с источником тока J₂, получим схему рис. 1.16, б, эквивалентное сопротивление которой R₁ + 1/G₂ как раз и будет равно внутреннему сопротивлению эквивалентного генератора, т.е. R_г = R₁ + 1/G₂. Для определения ЭДС этого генератора заменим источник тока J₂ с проводимостью G₂ эквивалентной ЭДС Е₂ = J₂/G₂ с сопротивлением R₂ = 1/G₂ (см. выше). Напряжение холостого хода (I = 0) для полученной схемы (рис. 1.16, в) будет, очевидно, равно U = E₁ – E₂. Таким образом схему, изображенную на рис. 1.16, а, можно заменить эквивалентным генератором, изображенным на рис. 1.15, б, с параметрами Е_г = E₁ – J₂/G₂, R_г = R₁ + 1/G₂. Заменяя отдельные подцепи, соединенные с остальной частью цепи только двумя узлами, подобными эквивалентными генераторами, можно существенно упростить расчет цепи.

В общем случае методика расчета сложной электрической цепи, основанная на замене ее отдельных подцепей более простыми подцепями (типа эквивалентных генераторов для двухполюсников), называется диакоптикой электрических цепей. Введенная в теорию электрических цепей Г. Кроном диакоптика является в настоящее время одной из наиболее востребованных практикой методикой их расчета.