§ 7. Применение вычислительной техники

Современное развитие вычислительной техники существенно упрощает и ускоряет процесс анализа опытных данных. Так, например, с помощью электронных таблиц можно облегчить решение вопроса о виде распределения на стадии проверки гипотезы по критерию Пирсона и по критерию Колмогорова.

Проиллюстрируем работу с электронными таблицами на конкретном примере.

Задание. Необходимо изучить изменение выработки на одного рабочего механического цеха в отчетном году по сравнению с предыдущим. Получены следующие данные о распределении 100 рабочих цеха по выработке в отчетном году (в процентах к предыдущему году): 119,0; 120,9; 121,5; 112,1; 134,7; 97,0; 125,6; 130,2; 97,8; 128,3; 99,1; 100,0; 100,9; 114,1; 105,6; 120,3; 102,4; 105,8; 132,9; 113,6; 100,1; 125,5; 122,2; 118,8; 119,9; 121,2; 123,3; 103,8; 135,6; 126,3; 112,1; 115,0; 120,0; 123,3; 120,8; 116,2; 106,5; 124,3; 123,5; 119,6; 120,0; 122,9; 121,0; 107,9; 129,9; 115,1; 116,3; 117,2; 108,2; 115,0; 124,9; 126,3; 128,3; 129,6; 131,6; 110,3; 125,5; 118,9; 120,0; 121,1; 107,6; 106,9; 129,6; 110,2; 119,0; 119,6; 111,8; 125,0; 131,8; 108,6; 117,2; 13,5; 119,6; 123,3; 107,3; 129,6; 133,3; 116,1; 113,6; 123,2; 128,7; 122,3; 115,4; 116,3; 113,0; 121,1; 122,0; 135,2; 108,4; 138,0; 126,0; 141,0; 126,4; 132,2; 136,9; 127,2; 126,1; 117,5; 116,2; 113,5.

Решение. Для решения воспользуемся электронными таблицами. Имеющиеся числовые данные внесем в первый столбец таблицы, затем выберем функцию «Сортировка и фильтр» и с помощью операции «Сортировка от минимума к максимуму» расположим элементы в порядке возрастания. В результате получим столбец, элементы которого выписаны в таблице 14.

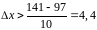Первый элемент в таблице является минимальным, а последний – максимальным. Т.о. , , тогда и .

_Берем . И заполняем таблицу 15. Первый и третий столбики таблицы заполняются вручную, а остальные с помощью задания формулы в первой строке и функции заполнить вниз. Три нижние строки заполняются в виде формул:

Таблица 14

97 97,8 99,1

100 100,1 100,9 102,4 103,8

105,6 105,8 106,5 106,9 107,3 107,6 107,9 108,2 108,4

108,6 110,2 110,3 111,8 112,1 112,1 113

113,54 113,6 113,6 114,1 115 115 115,1 115,4 116,1 116,2 116,2 116,3 116,3 117,2 117,2 117,5

118,8 118,9 119 119 119,6 119,6 119,6 119,9 120 120 120 120,3 120,8 120,9 121 121,1 121,1 121,2 121,5 122

122,2 122,3 122,9 123,2 123,3 123,3 123,3 123,5 124,3 124,9 125 125,5 125,5 125,6 126 126,1 126,3 126,3 126,4

127,2 128,3 128,3 128,7 129,6 129,6 1 29,6 129,9 1 30,2

131,6 131,8 132,2 132,9 133,3 134,7 135,2 135,6 136,9 138 141 141

Таблица 15

Интервалы	Середины интервалов	Часто-ты
95 – 99,5	97,25	3	291,75	1446,725
99,5 – 104	101,75	5	508,75	1524,258
104 – 108,5	106,25	9	956,25	1511,654
108,5 – 113	110,75	7	775,25	501,0012
113 – 117,5	115,25	16	1844	250,9056
117,5 – 122	119,75	20	2395	5,832
122 – 126,5	124,25	19	2360,75	482,6304
126,5 – 131	128,75	9	1158,75	819,1044
131 – 135,5	133,25	7	932,75	1379,851
135,5 – 140	137,75	3	413,25	1031,195
140 – 144,5	142,25	2	284,5	1061,683

Создадим еще один столбец, куда внесем . Выделив полученный столбец, обратимся к функции «Вставка», затем выберем пункт «Диаграмма» и далее - «гистограмма». В результате получим гистограмму, которая дает представление о графике плотности распределения случайной величины (см. рис.17).

95 99,5 104 108,5 113 117,5 122 126,5 131 135,5 140 144,5

Рис. 17

Чтобы построить график функции распределения создадим столбец , выделим его и затем выберем в пункте «Диаграмма» подпункт «График». Получим рис.18.

Рис.18

Доверительный интервал для математического ожидания случайной величины получаем следующий: .

Гистограмма опытных значений Х похожа на график плотности нормального распределения. По опытному значению коэффициента вариации (см. Приложение 2) распределение является нормальным. Высказываем нулевую гипотезу : Х имеет нормальное распределение с и . Проверим эту гипотезу на уровне значимости

_{В электронных таблицах заполним первый столбик значениями левых концов интервалов, а второй значениями правых концов, при этом в первую ячейку первого столбика поместим} , а в последнюю . Два первых интервала объединим в один, т.к. число элементов в первом интервале меньше 5. Два последних интервала объединим в один, так как число элементов в каждом из них меньше 5. В третий столбец внесем . Четвертый столбец заполняем обращаясь к заданию формулы с помощью следующей последовательности действий: выбираем «функция», «статистические», «норм.распр.». В качестве аргумента выбираем правый конец интервала, математическое ожидание и среднее квадратическое отклонение указываем в соответствии с задачей, логическое значение «истина». В пятом столбце подсчитаем , присвоив первому элементу значение , а далее

В шестом столбике зададим формулу . Подсчитав с помощью операции суммирования сумму элементов седьмого столбца, получим . Полученная таблица аналогична таблице 16.

Из таблицы распределения (см. Приложение 3) по уровню значимости и числу степеней свободы находим .

Таблица 16

Левый конец	Правый конец
	104	8	0,06413	0,06413	0,392733
104	108,5	9	0,142085	0,077955	0,186117
108,5	113	7	0,2673	0,125215	2,434776
113	117,5	16	0,432112	0,164812	0,01405
117,5	122	20	0,609878	0,177766	0,278099
122	126,5	19	0,766999	0,157122	0,687996
126,5	131	9	0,880801	0,113802	0,497816
131	135,5	7	0,948343	0,067543	0,008941
135,5		5	1	0,051657	0,005312
				1	4,50584

Сравнивая и , получаем, что < Следовательно гипотеза о нормальном распределении на выбранном уровне значимости подтверждается опытным путем. Т.о., с помощью критерия Пирсона, проверена гипотеза о нормальном распределении.

Проведем проверку, выдвинутой гипотезы с помощью критерия Колмогорова. Заполняем таблицу. Первый, второй, третий и четвертый столбцы заполняются также как и в случае критерия Пирсона. В пятом столбце подсчитываем , а в шестой столбец внесем . Получаем таблицу вида, аналогичного таблице 17.

Таблица 17

Левый конец	Правый конец
	104	8	0,06413	0,08	0,01587
104	108,5	9	0,142085	0,17	0,027915
108,5	113	7	0,2673	0,24	0,0273
113	117,5	16	0,432112	0,4	0,032112
117,5	122	20	0,609878	0,6	0,009878
122	126,5	19	0,766999	0,79	0,023001
126,5	131	9	0,880801	0,88	0,000801
131	135,5	7	0,948343	0,95	0,001657
135,5		5	1	1	0
					0,032112

Найдя максимальный из элементов шестого столбца, получаем =

По таблице из Приложения 5 находим критическое значение определенное на уровне значимости α=0,1: =1,22. Т.к. , то считают, что нулевая гипотеза о том, что случайная величина Х имеет заданный закон распределения, не противоречит опытным данным. Т.о. с помощью критерия Колмогорова проверена гипотеза о нормальном распределении.

Попробуем выдвинуть гипотезу, что рассматриваемая закономерность описывается показательным распределением. Воспользуемся критерием Пирсона. Заполним таблицу 18.

Таблица 18

Левый конец	Правый конец
0	104	8	0,582057	0,582057	43,30524
104	108,5	9	0,59754	0,015483	35,86484
108,5	113	7	0,612449	0,014909	20,35672
113	117,5	16	0,626806	0,014357	147,7483
117,5	122	20	0,64063	0,013825	250,7143
122	126,5	19	0,653943	0,013313	234,4986
126,5	131	9	0,666763	0,01282	46,46625
131	135,5	7	0,679108	0,012345	26,92749
135,5		5	1	0,320892	22,86831
				1	828,75005

Получаем, что . Из таблицы (см. Приложение 3) распределения по уровню значимости и числу степеней свободы находим . Сравнивая и , получаем, что > , следовательно гипотеза о показательном распределении на выбранном уровне значимости отвергается опытным путем. Т.о. с помощью критерия Пирсона отвергнута гипотеза о показательном распределении.

Проведем проверку, выдвинутой гипотезы с помощью критерия Колмогорова. Заполняем таблицу.

Таблица 19

Левый конец	Правый конец
0	104	8	0,582057	0,08	0,502057
104	108,5	9	0,59754	0,17	0,42754
108,5	113	7	0,612449	0,24	0,372449
113	117,5	16	0,626806	0,4	0,226806
117,5	122	20	0,64063	0,6	0,04063
122	126,5	19	0,653943	0,79	0,136057
126,5	131	9	0,666763	0,88	0,213237
131	135,5	7	0,679108	0,95	0,270892
135,5		5	1	1	0
					0,502057

Найдя максимальный из элементов шестого столбца, получаем =0,502 =5,02.

По таблице из Приложения 5 находим критическое значение определенное на уровне значимости α=0,1: =1,22. Т.к. , то считают, что нулевая гипотеза о том, что случайная величина Х имеет заданный закон распределения, противоречит опытным данным. Т.о. с помощью критерия Колмогорова гипотеза о показательном распределении также отвергнута.

Ответ: данный набор значений случайной величины описывается с помощью нормального распределения.

Рассмотренный выше пример не только проиллюстрировал способ решения задачи с использованием электронных таблиц, но также показал, как отвергается неверно выдвинутая гипотеза.