9. Доверительный интервал для оценки среднего

квадратического отклонения нормального распределения

Пусть случайная величина имеет нормальное распределение. Доверительный интервал, покрывающий среднее квадратическое отклонение этого признака с доверительной вероятностью γ, находится из условия , если , , если , где находится по данным и γ из таблицы значений .

§ 3. Проверка статистических гипотез

В некоторых случаях требуется знать закон распределения генеральной совокупности, который неизвестен, однако есть основания предполагать, что он имеет определенный вид (например, экспоненциальный). Тогда выдвигается гипотеза: генеральная совокупность распределена по экспоненциальному закону.

В других случаях закон распределения известен, но неизвестны его параметры. Если есть основания предполагать, что неизвестный параметр равен определенному значению , то выдвигается гипотеза = .

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Наряду с данной гипотезой рассматривают и противоречащую ей гипотезу. В случае, когда выдвинутая гипотеза отвергается, обычно принимается противоречащая ей гипотеза.

Нулевой (основной) называют выдвинутую гипотезу . Конкурирующей (альтернативной) называют гипотезу , которая противоречит основной. Например, если нулевая гипотеза : математическое ожидание нормально распределенной величины равно 10, т.е. , тогда гипотеза может иметь вид .

Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому различают ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

В целях проверки нулевой гипотезы в рассмотрение вводят специально подобранную случайную величину, распределение которой известно. Ее обозначают U или Z, если она распределена нормально, F или – по закону Фишера, T - по закону Стьюдента, - по закону хи-квадрат. Для общности ее можно обозначить K.

Случайную величину K, которая служит для проверки нулевой гипотезы, называют статистическим критерием. Например, если проверять гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий. Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперед неизвестные значения, и распределена по закону Фишера.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин, а затем и сам критерий и таким образом получают частное (наблюдаемое) значение критерия.

Наблюдаемым значением 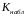называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивается на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают.

Поскольку критерий K – одномерная случайная величина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.

Критическими точками (границами) называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством , где – положительное число.

Левосторонней называют критическую область, определяемую неравенством , где – отрицательное число.

Односторонней называют правостороннюю или левостороннюю критическую область.

Двусторонней называют критическую область, определяемую неравенствами , где .

Для отыскания правосторонней критической области достаточно найти критическую точку. Для её нахождения задаются достаточно малой вероятностью – уровнем значимости . Затем ищут критическую точку , исходя из требований, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий K примет значение, большее (в случае правосторонней области), была равна принятому уровню значимости: .

Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию. Когда критическая точка уже найдена, вычисляют по данным выборок наблюдаемое значение критерия и, если окажется, что , то нулевую гипотезу отвергают; если же , то нет оснований, чтобы отвергнуть нулевую гипотезу.

Замечание. Наблюдаемое значение критерия может оказаться большим не потому, что нулевая гипотеза ложная, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости . Вопрос о том, каким выбрать , определяется значимостью последствий ошибки первого рода. Чем серьезнее эти последствия, тем меньше должен быть уровень значимости . Однако слишком малым число тоже брать нельзя, т.к. при малых становится большой вероятность принять неверную нулевую гипотезу, что является ошибкой второго рода и это тоже нежелательно. Если нулевая гипотеза принята, то ошибочно думать, что она доказана. Более правильно говорить «данные наблюдений согласуются с нулевой гипотезой и, следовательно, не дают оснований ее отвергать». На практике для большей уверенности принятия гипотезы ее проверяют другими способами или повторяют эксперимент, увеличивая объем выборки.