Міністерство освіти і науки, молоді та спорту НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ «ЛЬВІВСЬКА ПОЛІТЕХНІКА»

Кафедра ІТВС

Лабораторна робота № 2

“ Робота в просторовій системі координат”

З дисципліни “Комп’ютерна графіка”

Виконав ст. групи КН-______

_________________________

Прийняв__________________

Львів – 2013

Мета роботи: Ознайомлення з основами комп‘ютерної графіки в просторовій системі координат.

Теоретичні основи

2.1 Вступ

Для кращого сприйняття форми об’єкта необхідно мати його зображення в тривимірному просторі. У багатьох випадках наочне представлення про об’єкт можна одержати шляхом виконання операцій обертання і переносу, а також побудови проекцій. Введемо однорідні координати. Точка в тривимірному (x y z) просторі задається чотиримірним вектором (x y z 1) або ж (X Y Z H). Перетворення з однорідних координат описується співвідношеннями:

(2.1)

де T - деяка матриця перетворення.

Ця матриця може бути представлена у вигляді 4 окремих частин:

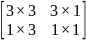
Матриця 3x3 здійснює лінійне перетворення у виді зміни масштабу, зсуву й обертання. Матриця-рядок 1х3 робить перенос, а матриця-стовпець 3х1 - пере­творення в перспективі. Останній скалярний елемент виконує загальну зміну масштабу. Повне перетворення, отримане шляхом впливу на вектор положення матрицею 4x4 і нормалізації перетвореного вектора, будемо називати білінійним перетворенням. Воно забезпечує виконання комплексу операцій зсуву, часткової зміни масштабу, обертання, відображення, переносу, а також зміни масштабу зображення в цілому.

2.2 Тривимірна зміна масштабу

Діагональні елементи основної матриці перетворення 4х4 здійснюють часткову і повну зміну масштабу. Розглянемо перетворення, яке робить часткову зміну масштабу:

(2.2)

Загальна зміна масштабу визначається матрицею перетворення:

(2.3

Зменшення масштабу можна досягнути при рівних коефіцієнтах часткових змін масштабів:

(2.4)

На рис.2.1 показане масштабне збільшення куба в три рази (s=3). Зменшення масштабу представлене на рис. 2.2. У цьому випадку у матриці перетворення (2.4) s=2.

Рис. 2.1 Збільшення куба у 3 рази Рис. 2.2 Зменшення куба у 2 рази

2.3 Перетворення тривимірних координат в двовимірні

Нехай в тривимірному середовищі точка задана координатами (x,y,z). При переході у двовимірне середовище маємо:

x=x-z*sinθ

y=y-z*sinθ, де θ -це кут між осями x та z (рис. 2.3).

Рис. 2.3 До перетворення координат

2.4 Тривимірний зсув

У загальній матриці перетворення розміру 4х4 (2.1) її недіагональні елементи верхньої лівої підматриці 3х3 здійснюють зсуви у трьох вимірах, тобто: .

(2.5)

2.5 Тривимірні обертання

Для обертання на кут θ навколо осі y - нулі ставлять у другому рядку і другому стовпці матриці перетворення, за винятком одиниці на головній діагоналі. Повна матриця задається виразом (2.6):

Т = (2.6)

Аналогічно матриця перетворення для обертання на кут θ навколо осі z має вид (2.7):

Т = (2.7)

Приклади обертання фігури навколо осі у приведено на рис. 2.5, навколо осі z –на рис.2.4, навколо осі x–на рис.2.6.

Рис. 2.4 Bідносно Z Рис. 2.5 Bідносно Y Рис. 2.6 Bідносно X

Аналіз визначників для матриць (2.5)-(2.6) показує, що для будь-якої матриці обертання її детермінант дорівнює +1.

Зауваження:

Обертання фігур описуються множенням матриць, а це значить, що тривимірні обертання некомутативні, тобто порядок множення буде впливати на кінцевий результат.

Наприклад, обертання навколо осі х, за яким наступає обертання на такий же кут θ навколо осі y. Використовуючи рівняння (2.5) і (2.6), одержимо:

T= (2.8)

Зворотна послідовність дій, тобто обертання навколо осі y і наступне за ним обертання на такий же кут навколо осі x дає:

Т = (2.9)