Реальные газы.

Реальные газы состоят из атомов, которые в свою очередь состоят из заряженных ядер, вокруг которых вращаются заряженные частицы – электроны. Между ними действуют электрические силы, радиус действия которых неограничен.

В разделе «электродинамика» рассматривались такие системы («Дипольный момент системы»), где - дипольный момент молекулы.

.

Вывод: вокруг реальных молекул существуют реальные электрические поля. Таким образом, в реальном газе пренебрегать взаимодействием между молекулами нельзя.

Это взаимодействие характерно тем, что на больших расстояниях преобладают силы притяжения, которые на небольших расстояниях, сравнимых с размерами молекул, переходят в силы отталкивания.

Притяжение молекул характеризуется уменьшением потенциальной энергии (потенциальная энергия определяется работой, которую нужно совершить, чтобы систему создать).

Данный график отражает зависимость потенциальной энергии от расстояния.

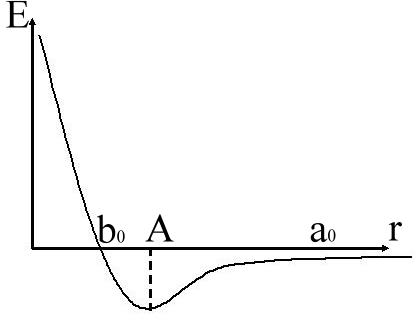
Получим выражение для свободной энергии реального газа.

.

,

- элемент объема, связанный с пространственными координатами.

.

- см. рисунок предыдущей лекции.

- такое расстояние, на котором силы притяжения начинают заметно проявляться, - расстояние, сравнимое с размерами молекул, - наибольшее из отрицательных по модулю значений потенциальной энергии взаимодействия.

,

.

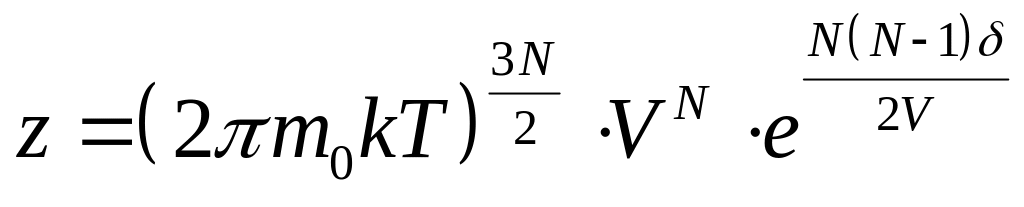Найдем давление

,

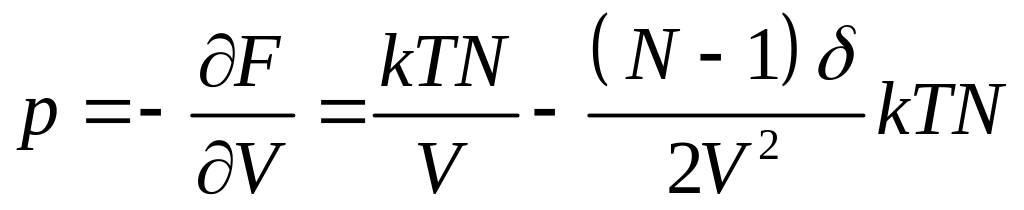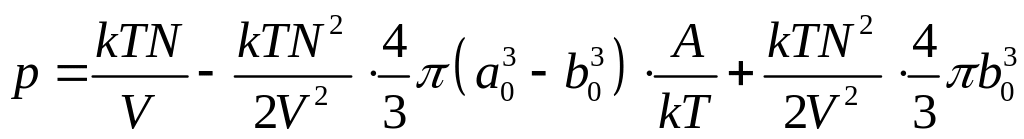
Т. к. :

(*)

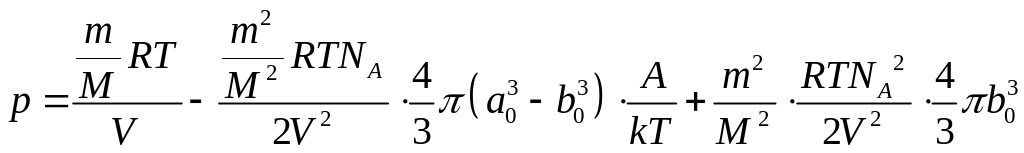В курсе общей физики для реальных газов экспериментально дается уравнение Ван-дер-Ваальса.

Для реального газа

,

- некоторые константы, значения которых для различных газов установлены.

Выразим из этого выражения давление.

. (**)

Сравним (*) и (**), по признаку знаков соотнесем слагаемые.

,

,

Физический смысл - половина реального объема молекул в одном моле.

Вывод: макроскопический параметр выразили через микроскопический .

Аналогично можно выразить через , приравняв два других слагаемых.

Лекция 11

Квантовая статистика.

Аппарат квантовой механики описывает вероятность нахождения частицы в некоторой области пространства в некоторый момент времени с помощью волновой функции - вероятность того, что частица, находящаяся в некотором объеме в некоторый момент времени , определяется с помощью квадрата модуля волновой функции.

.

Таким образом, квантовая механика по самой своей сути носит статистический характер, т. е. глубинно связана со статистической физикой.

В отличие от классической физики в квантовой модели проявляется ряд специфических закономерностей. Выделим наиболее важные из них:

1. В квантовой механике выполняется принцип неопределенности Гейзенберга, согласно которому , и - неопределенности в задании импульса и координаты.

а) Из этого принципа вытекает, что классическое понятие траектории движения частицы в квантовой не выполняется.

б) Две частицы, находящиеся в некотором замкнутом объеме, принципиально различить невозможно.

При движении частиц, и попытке наблюдать эти частицы, неизбежно наступает момент, когда расстояние между частицами окажется сравнимым с , т. е. с неопределенностью в задании координаты, и, начиная с этого момента, мы теряем идентификацию частиц.

Этот принцип называется принципом тождественности квантовых частиц.

2. В классической физике значения физических величин, описывающих поведение частицы, таких как энергия, импульс, момент импульса носят непрерывный характер, т. е. с течением времени изменяются непрерывно.

В квантовой физике эти величины могут принимать только разрешенный набор дискретных значений. Так возможные значения энергии получаются из решения уравнения Шредингера.

С учетом того, что рассматривается идеальный одноатомный квантовый газ, выражение для энергии газа можно записать

,

Где - те значения энергии, которые могут быть у частиц.

Для всех частиц этот набор одинаков, полученный из уравнения Шредингера, - число частиц, который в данный момент времени имеют соответствующие значению энергии.

- энергия системы в некоторый момент Z.

С течением времени значение Е у частиц изменится. Это будет соответствовать другому состоянию с другим заполнением квантовых уровней.

Вероятность того, что система находится в состоянии

F* - свободная энергия квантовой системы.

Сумма вероятностей нахождения системы в различных состояниях = 1:

Вынесем

- аналогично интеграл состояния называется статистической суммой.

Если спектр энергетических значений состоит из очень большого числа близко расположенных значений уровней, то

В силу того, что квантовые частицы неразличимы, число состояний по сравнению с классическим газом уменьшается в N! раз.

В силу принципа неопределенности если распишем dГ как было в классической модели.

но таких произведений N штук получим

- min возможный объем в пространстве Г, в пределе которого можно выделить конкретное состояние системы (оно будет отличатся от состояния, находящееся в соседнем элементарном объеме).

В случае классической модели dГ – будет связано с произвольными действиями деления объема на число частиц, в этом был определенный произвол.

Число состояний изменится за счет уточнения (определения) выбора min фазового объема, который является

Поэтому в окончательном виде в квантовой модели

Лекция 12

- для бозонов распределения Базе.

- энергия соответствующего квадрату уравнения, на котором находятся частицы;

- химический потенциал;

к – постоянная Больцмана;

Т – температура.

- для фермионов распределение Ферми.

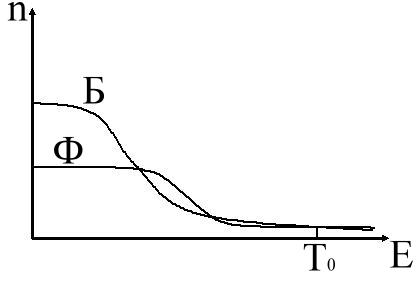
При некоторой температуре Т₀ (характеристическая температура).

Различие между распределениями исчезает, т.е. начинают вести себя одинаково. Т₀ еще называют температурой возрождения. При этой температуре различие между бозонами и фермионами исчезает и их поведение приблизительно равно классическому для металла Т₀ = 10⁴К для полупроводников Т₀ = 10⁰К, у реальных газов – несколько К.

Лекция 13