Второй закон термодинамики и следствия из него.

Рассмотрим изолированную систему. Тогда в изолированной системе, находящейся в равновесном состоянии или в случае происходящих обратимых процессов .

Рассмотрим случай, когда в изолированной системе происходит необратимый процесс . Такой процесс будет сопровождаться ростом энтропии.

Покажем, что переход теплоты от горячего тела к холодному происходит в соответствии со вторым законом термодинамики.

Пусть имеются два тела (первое разогретое, второе холодное), при этом . Установим между ними тепловой контакт.

Г ипотетически возможны 2 случая:

1. Некоторое количество теплоты переходит от горячего тела к холодному.

(т. к. произошло понижение количества теплоты первого тела), .

Изменение энтропии в целом:

;

2. 

Соотнесем эти выражения со вторым законом термодинамики:

в первом случае , а во втором .

Следовательно, первый процесс соответствует второму закону термодинамики.

Пусть имеется сосуд с газом. Этот сосуд разделен на две половинки, причем газ изначально находится в одной половинке.

Убираем перегородку, и газ самопроизвольно заполняет весь объем.

Мы предположили, что обмена энергией с окружающей средой не происходит. Поэтому внутренняя энергия не меняется.

Энтропия – это функция состояния, поэтому неважно, каким путем система пришла в новое состояние. Можно предположить, что процесс происходил изотермически.

При изотермическом расширении газа . Тогда:

Воспользуемся уравнением Менделеева :

.

Тогда согласно второму закону термодинамики:

.

Допустим :

.

Процесс расширения газа соответствует второму закону термодинамики, энтропия системы при этом возрастает.

Обратный процесс сопровождался бы уменьшением объема, который занимает газ. Но тогда , а, следовательно, приращение энтропии отрицательно, а это противоречит второму закону термодинамики.

Увеличение энтропии в системе сопровождается увеличением хаоса и уменьшением порядка.

Это отражает диаграмма:

Третий закон термодинамики (или теорема Нернста).

Третий закон термодинамики констатирует, что при абсолютном нуле энтропия равна нулю.

При абсолютном нуле движение атомов останавливается (например, в кусочке льда) и система реализуется только лишь через одно состояние.

Согласно теореме Нернста:

, а должна обратиться в ноль.

.

Лекция 9

Теплоемкость идеальных газов.

Теплоемкостью тела называется количество теплоты, которое надо сообщить телу, чтобы изменить его температуру на .

Существуют понятия удельной теплоемкости (когда нагревается тело массой 1кг) и молярной теплоемкости (когда нагревается вещество в количестве одного моля).

Воспользуемся первым законом термодинамики:

Согласно введенному определению:

Различают 2 случая:

1) .

Учитывая :

.

Тогда

,

, где - число степеней свободы.

Если речь идет о молярной теплоемкости:

.

2) .

.

Воспользуемся уравнением Менделеева( ):

Следовательно, не зависят от температуры у идеальных газов.

Для реальных одноатомных газов это почти так (например, ).

А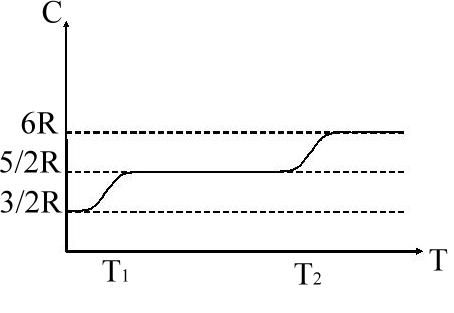 вот для двухатомных газов (например, )

в достаточно большом интервале температур газ действительно не зависит от . Однако, при более низких либо достаточно высоких происходит изменения теплоемкости.

Объяснить эти явления в рамках классической физики оказалось невозможным.

Лекция 10