Обратимые и необратимые процессы.

С понятием обратимого и необратимого процессов тесно связано понятие нахождения системы в равновесном и неравновесном состояниях.

В дальнейших рассуждениях полагаем: система находится в равновесном состоянии, если молекулы этой системы подчиняются распределению Максвелла. В равновесном состоянии система может находиться бесконечно долго. Переход от одного равновесного состояния системы к другому происходит в общем случае с нарушением равновесного состояния.

Через некоторый промежуток времени в системе вновь устанавливается новое равновесное состояние. Очень важным моментом является переход от одного равновесного состояния к другому. Если такой процесс происходит быстро, то он необратимый.

Рассмотрим пример с поршнем.

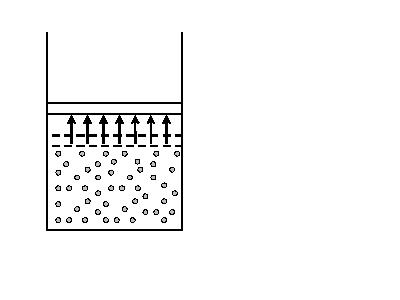В начальный момент газ находится в равновесном состоянии. Сразу после резкого выдвижения поршня образуется разреженная область пространства, в которой нет молекул. Это приводит к тому, что часть молекул из верхнего слоя газа начинает двигаться в направлении поршня (происходит нарушение распределения Максвелла по скоростям).

Принципиально этот процесс в обратном порядке провести невозможно. Поэтому такой процесс необратимый.

Можно поступить по-другому: выдвигать поршень чрезвычайно медленно, так чтобы молекулы, находящиеся рядом с поршнем, «не заметили» этого. Хаотическое движение молекул в целом не нарушается. Через определенный промежуток времени поршень так же медленно вернуть обратно, состояние газа при этом не изменится. Такие процессы называются обратимыми или квазистационарными.

В школьной физике рассматриваются только квазистационарные процессы.

Рассмотрим термодинамический цикл, состоящий из четырех квазистационарных процессов, так называемый цикл Карно.

Лекция №6.

Цикл Карно.

Цикл Карно состоит из двух изотерм и двух адиабат ( ).

1 -2, 3-4 – изотермы; 2-3, 4-5 – адиабата.

,

На участке 1-2 все подведенное количество теплоты превращается в работу.

2-3: ,

3-4: изотерма, но при температуре ,

4-1: (работа, которую совершила машина.)

Найдем КПД этой тепловой машины.

для адиабаты.

- из курса общей физики.

для точек 2 и 3.

для точек 1 и 4.

- КПД цикла Карно.

Т. о. КПД машины Карно в принципе не зависит от рабочего тела (газа), а зависит только от температуры нагревателя и температуры холодильника .

Сразу отметим, что из полученного результата вытекают важные следствия.

Следствие 1.

Невозможно в природе все количество теплоты превратить в работу. Это можно объяснить тем, что с количеством теплоты связывается энергия хаотического движения молекул.

Совершение работы всегда связано с изменением объема. А изменение объема сопровождается появлением элементов упорядоченного движения, т.е. работе можно сопоставить возникновение упорядоченного движения молекул.

Само по себе хаотическое движение в упорядоченное никогда не переходит. А упорядоченное в хаотическое переходит самопроизвольно (ответ на этот вопрос связан со вторым законом со вторым законом термодинамики).

Стало ясно, что количество теплоты и работа это не форма энергии, а способы перехода из одной энергии в другую.

Мощность машины Карно равна нулю, т.к. процессы обратимые и поршень перемещается как угодно медленно.

Машина носит чисто теоретический характер, но КПД самый большой.

Докажем, что КПД самый большой. Рассмотрим диаграмму , где - энтропия.

Допустим, что в этих же интервалах температур и энтропий работает другая тепловая машина. Контур этой машины .

КПД полезного действия Карно самый большой.

Следствие 2.

Для обратимых: .

Т.о. Клазиус высказал предположение о существовании , в последствии названной энтропией.

Следствие 3.

Цикл Карно позволяет подойти ко второму закону термодинамики, а именно, цикл Карно будет существовать для необратимых процессов (поршень движется быстро).

За счет быстрого движения поршня молекулы окружающей среды получают кинетическую энергию и уносят безвозвратно в окружающее пространство.

Это может привести только к уменьшению КПД

или - второй закон термодинамики.