(Интеграл Пуассона)
(1)
- выражение
для свободной энергии идеального
одноатомного газа.
Уравнение состояния идеального одноатомного газа.
Энергия газа в самом общем случае складывается из кинетической энергии молекул, потенциальной за счет взаимодействия с внешним полем и потенциальной энергии при взаимодействии молекулы со стенками сосуда (кинетическая энергия переходит в потенциальную энергию молекулы и стенки).
Выделим направление
вдоль оси
,
возьмем производную по
:
При изучении
механики было показано
.
,
где
- полная энергия.
.
- площадь грани сосуда, перпендикулярный оси .
.
Воспользуемся интегралом по Г – пространству.
.
Возьмем производную
по
.
- уравнение
состояния.
В общем случае уравнением состояния называется уравнение, которое связывает три макроскопических состояния.
Найдем выражение для давления идеального газа с учетом формулы для .
- закон Менделеева.
Лекция 6
Физический смысл свободной энергии.
Проанализируем
выражение для
.
Если
постоянно, то свободная энергия зависит
от
и
.
Из формулы (1) следует, что значения
энергии зависят только от
и
.
Можно выполнять разные процессы, переводя
газ из одного состояния в другое. Но
если мы вернемся в начальное состояние,
то и значение энергии будет тем же самым.
Такие функции называют функциями состояния.
.
Воспользуемся
.
Тогда
,
.
Рассмотрим изотермический процесс:
.
Только в изотермическом
процессе
- элемент работы:
.
Т.о. в изотермическом процессе изменение свободной энергии равно работе системы с противоположным знаком.
Основное тождество. (уравнение Гиббса - Гельмгольца).
Будем исходить из
:
Возьмем производную по температуре:
- внутренняя
энергия.
.
Мы рассматриваем равновесное состояние газа, при котором макроскопические параметры не меняются, сколько бы раз ни повторяли измерения.
Экспериментальные результаты для равновесного состояния совпадают с их средними значениями. На этом основании значки средних значений можно убрать.
.
- основное
тождество.
Лекция 7
- энтропия.
-
другая формулировка основного тождества.
Пока будем рассматривать как функцию состояния, физический смысл которой будет выяснен дальше.
Запишем выражение для дифференциала внутренней энергии:
.
Из первого закона
термодинамики
- термодинамический
смысл энтропии
– это такая функция состояния, бесконечно
малое изменение которой равняется
отношению бесконечно малого количества
теплоты, сообщаемого системе к температуре,
при которой это происходит.
Предполагается, что температура системы остается величиной постоянной
Статистический смысл энтропии.
Из уравнения Гиббса – Гельмгольца:
.
Обозначим
;
,
и, т. к. функция распределения
,
используем выражение для среднего:
.
Записанное выражение отражает статистический смысл энтропии. Энтропия прямо пропорциональна среднему значению логарифма функции распределения.
Анализируя статистический смысл энтропии, рассмотрим следующий пример.
Допустим, есть два
объема:
,
причем в объемах содержится одинаковое
количество молекул
.
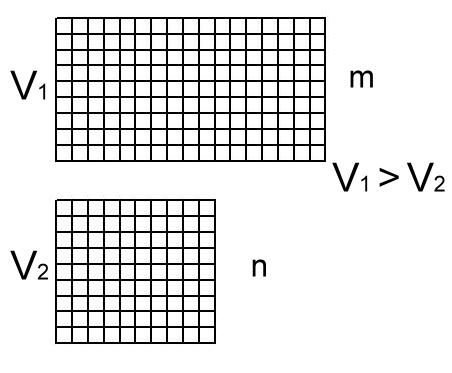
Введем достаточно
маленький объемчик
и разобьем
и
на такие элементарные объемы.
В первом случае
получим
-ячеек,
во втором
-ячеек.
Одну молекулу можно распределить
-способами
в
и
-способами
в
.
Тогда в первом
случае:
,
во втором:
.
Найдем отношение
.
,
(2)
.
.
Рассмотрим переход газа при изотермическом процессе от до :
(первый закон
термодинамики).
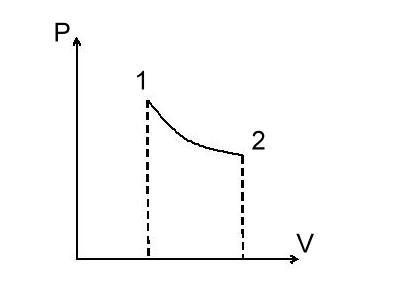
В изотермическом
процессе
,
,
Из уравнения
Менделеева:
,
,
,
.
Чтобы было соответствие с рисунком, переобозначим точки:
(3)
.
Сравним (2) и (3).
Домножим обе части
(2) на
:
Энтропия пропорциональна числу возможных способов размещения в объеме.
Число возможных различных состояний будем называть термодинамической вероятностью.
Лекция 8