Статистическая физика.
Лекция №1.
Введение.
Одним из основных понятий статистической физики является понятие «идеального газа». В рамках классической модели под идеальным газом будем понимать газ из мельчайших частиц – молекул, которые находятся в состоянии прямолинейного равномерного движения. В идеальном газе взаимодействие между молекулами на расстоянии отсутствует.
Между молекулами возможны и происходят абсолютно упругие удары, при которых частицы обмениваются энергией (потерь энергии не происходит). В общем случае частицы находятся в состоянии хаотического движения, скорости частиц меняются непредсказуемым образом.
Объектом рассмотрения будет являться идеальный газ, находящийся в замкнутом объеме, при этом температура окружающей среды полагается неизменной (система находится в термостате). В такой системе распределение частиц по скоростям остается неизменным, хотя скорости отдельно взятых молекул меняются.
Нашей задачей является получение аналитического выражения этой зависимости.
Максвелловское распределение молекул по скоростям в идеальном газе.
Введем декартово
пространство скоростей. Выделим некоторый
интервал скоростей
.
Какова вероятность
того, что произвольно выбранная молекула
будет иметь проекцию скорости, попадающую
в этот интервал? Обозначим эту вероятность
,введем
функцию
.
Тогда вероятность будет зависеть от:
.
(*)
Рассуждая аналогичным образом для других проекций:
:
;
:
.
Выделим на рисунке
соответствующую область. Запишем
выражение
того события,
сто произвольно выбранная молекула
попадает в объем
:
.
Учитывая, что значения проекций скоростей молекул друг от друга не зависят, то вероятность того, что значения проекций в некоторый момент времени попадают в указанные интервалы, можно записать:
- согласно закону
теории вероятности, как 3 независимых
друг от друга события.
.
С другой стороны:
.
Предположим:
.
Тогда оба требования удовлетворяются:
.
Выражение
через экспоненту противоречит смыслу
выражения (*), т. к. с ростом скорости
возрастает и вероятность
,
что в действительности не так.
Установить данное
противоречие можно, поставив знак «-»:
.
Тогда с возрастанием скорости вероятность будет уменьшаться.
В математике
известен
- интеграл Пуассона.
Проинтегрируем выражение (*):
.
Данный интеграл
отражает вероятность того события, что
значение
у произвольно выбранной молекулы будет
находиться в пределах
.
Очевидно, что вероятность этого события
равна 1. поэтому разделим обе части этого
равенства на правую часть:
,
.
Аналогичные рассуждения справедливы для двух других проекций.
;
;
;
.
Где - функция распределения.
Для выяснения вида
параметра
проведем следующие рассуждения: сделаем
рисунок объема, в котором находится
газ. Выделим некоторую молекулу, у
которой проекция скорости
,
находящаяся недалеко от боковой грани
.
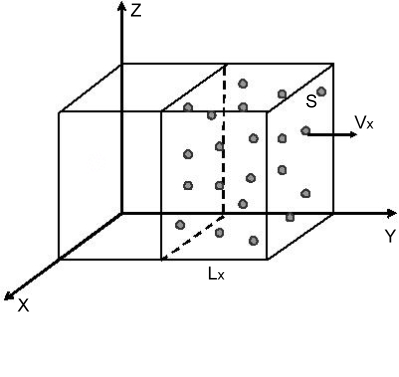
Предположим, что
на своем пути молекула не испытывает
соударений. Т. к. удар абсолютно упругий,
то изменение импульса у частицы после
удара будет
.
Из школьного курса
(II
закон Ньютона):
,
;
;
.
Где
- сила, с которой молекула действует на
стенку,
- время.
;
.
Моменту времени
можно поставить в соответствие некоторое
расстояние
.
Условно выделим на рисунке соответствующее
расстояние
и объем. В выделенном объеме кроме
выбранной нами молекулы существует еще
много других молекул, проекция скорости
которых
.
Лекция №2.
Обозначим число
таких молекул
.
Тогда
,
где
– число молекул в этом объеме.
,
.
Давление, которые создают эти молекул
.
За этот же промежуток времени о грань ударяют молекулы и с другими скоростями. Поэтому давление от всех молекул
.
Для решения этого интеграла воспользуемся интегралом Пуассона
.
Это выражение можно рассмотреть как функцию . Возьмем производную по этому параметру
.
Учитывая, что подынтегральная функция четная, можно записать
.
Тогда
,
.
В курсе школьной и общей физики рассматривается самостоятельно молекулярно-кинетическая теория. В этой модели есть определение давления, температуры.
.
Приравняем полученное выражение для давления с выражением для давления в молекулярно-кинетической теории и выразим
.
Параметр отражает свойства молекулы, а именно маску и свойства окружающей среды – температура.
Таким образом, функция распределения Максвелла полностью определена.
Найти среднее
значение
(квадрат модуля).
Для решения этой задачи необходимо знать функцию распределения по модулю скоростей. Для её решения целесообразно перейти в сферическую систему координат пространства скоростей.
В пространстве v роль полярного радиуса выполняет модуль вектора v.
- проинтегрируем
по
Полученное
выражение
- вероятность того, что модуль скорости
произвольно выбранной молекулы попадает
в промежуток
.
Т.е. в тонкий шаровой слой толщиной
.
Это и есть то, что мы искали.
Искомая функция распределения по модулю v.
Лекция 3