
2. Линеаризация связи с целью повышения качества прогноза
Коэффициент корреляции учитывает лишь линейную компоненту связи двух переменных. Поэтому для повышения качества проноза можно переменную, по которой строится прогноз, преобразовать так, чтобы характер связи был более линейный.
Изучим характер связи возраста и риска повторного кровотечения, для чего округлим переменную Возраст с шагом в 10 лет и рассчитаем совместное распределение с рецидивом.
Получаем следующее:
ВОЗР10 * REZIDIVE Crosstabulation
|
|
|
REZIDIVE |
|
Total |
|
|
|
1 |
2 |
|
ВОЗР10 |
10,00 |
Count |
4 |
1 |
5 |
|
|
% within ВОЗР10 |
80,0% |
20,0% |
100,0% |
|
20,00 |
Count |
31 |
15 |
46 |
|
|
% within ВОЗР10 |
67,4% |
32,6% |
100,0% |
|
30,00 |
Count |
93 |
32 |
125 |
|
|
% within ВОЗР10 |
74,4% |
25,6% |
100,0% |
|
40,00 |
Count |
105 |
41 |
146 |
|
|
% within ВОЗР10 |
71,9% |
28,1% |
100,0% |
|
50,00 |
Count |
87 |
26 |
113 |
|
|
% within ВОЗР10 |
77,0% |
23,0% |
100,0% |
|
60,00 |
Count |
45 |
40 |
85 |
|
|
% within ВОЗР10 |
52,9% |
47,1% |
100,0% |
|
70,00 |
Count |
21 |
24 |
45 |
|
|
% within ВОЗР10 |
46,7% |
53,3% |
100,0% |
|
80,00 |
Count |
2 |
13 |
15 |
|
|
% within ВОЗР10 |
13,3% |
86,7% |
100,0% |
|
90,00 |
Count |
1 |
1 |
2 |
|
|
% within ВОЗР10 |
50,0% |
50,0% |
100,0% |
Total |
|
Count |
389 |
193 |
582 |
|
|
% within ВОЗР10 |
66,8% |
33,2% |
100,0% |
Видно, что реально риск кровотечения (2) начинает линейно повышаться после 60. При этом он равен ½ в последней категории, за 90, но там – всего 2 человека, так что на отклонение от общей линии внимания обращать не надо.
Следовательно, реальным фактором риска является не возраст, а число лет, пережитых после 60.
Рассчитаем число лет, пережитых после 60

И рассчитаем прогноз по ней:
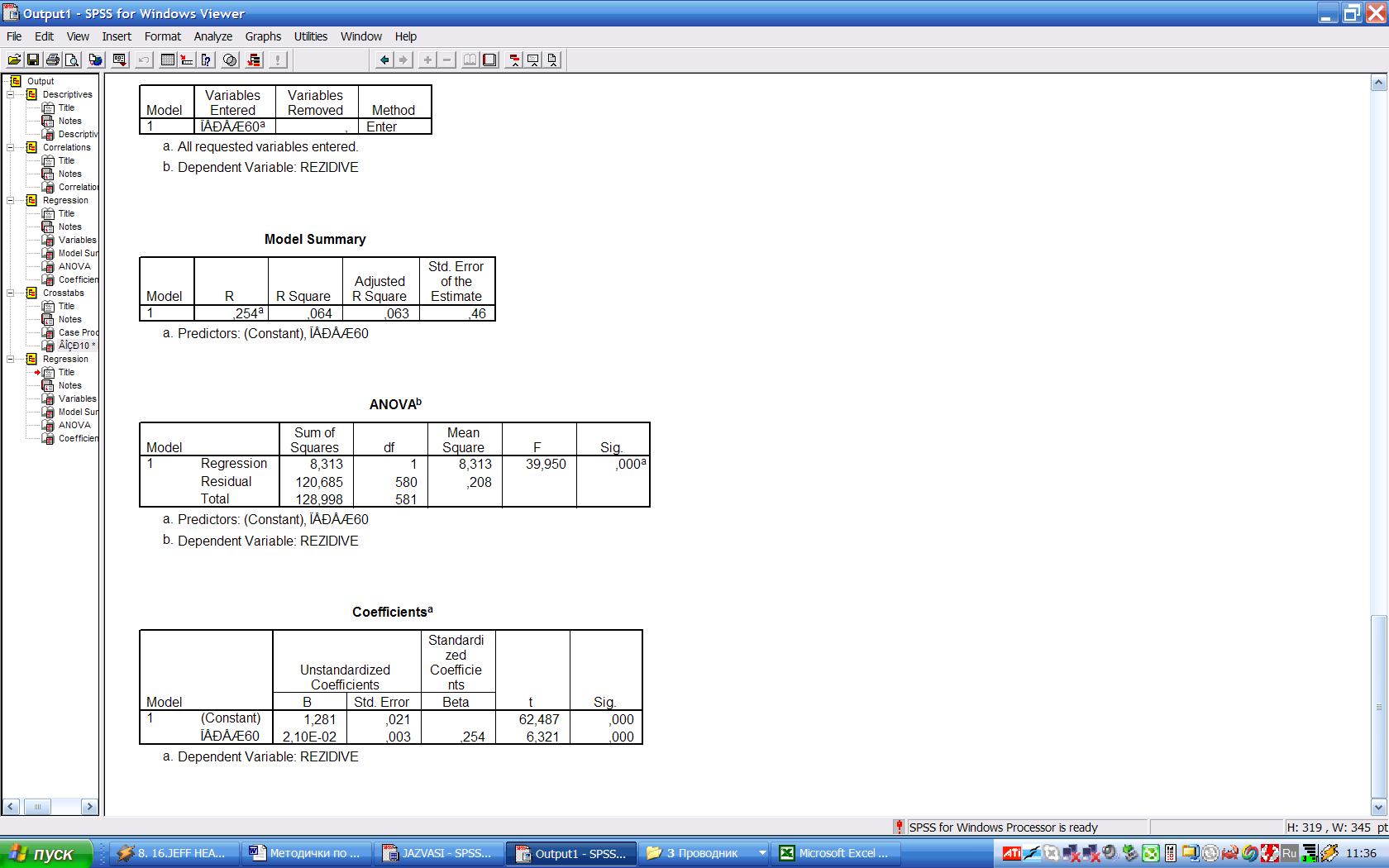
Видно, что теперь поправленный квадрат коэффициента корреляции вырос до 0,063. Из таблицы коэффициентов мы получаем, что каждый год, пережитый за 60, добавляет 2,1% к риску кровотечения.
Характер линеаризации зависит от характера связи. В том случае, если переменная, по которой строится прогноз, имеет 2 значения (например, пол), линеаризация не проводится – любое переопределение не меняет величину корреляционной связи.
В том случае, если у переменной, по которой строится прогноз, имеется несколько значений, для переопределения можно использовать условные средние.
Например, рассмотрим условные средние переменной rezidive в зависимости от цвета кожи при поступлении
Report
REZIDIVE
KOGAOKR |
Mean |
N |
Std. Deviation |
1 |
1,14 |
151 |
,35 |
2 |
1,37 |
403 |
,48 |
3 |
1,80 |
10 |
,42 |
Total |
1,32 |
564 |
,47 |
В качестве линеаризации можем взять новую переменную, которая вычисляется следующим образом:

Рассчитаем коэффициент корреляции рецидива с исходным и линеаризованным цветом кожи:
Correlations
|
|
REZIDIVE |
KOGAOKR |
KOGALIN |
REZIDIVE |
Pearson Correlation |
1,000 |
,255 |
,260 |
|
Sig. (2-tailed) |
, |
,000 |
,000 |
|
N |
582 |
564 |
564 |
KOGAOKR |
Pearson Correlation |
,255 |
1,000 |
,979 |
|
Sig. (2-tailed) |
,000 |
, |
,000 |
|
N |
564 |
564 |
564 |
KOGALIN |
Pearson Correlation |
,260 |
,979 |
1,000 |
|
Sig. (2-tailed) |
,000 |
,000 |
, |
|
N |
564 |
564 |
564 |
В данном случае сила связи увеличилась, но не очень сильно, так как исходная связь и так была достаточно близка к линейной.
Особенно существенно подобное предобразование там, где связь немонотонна.
Откроем файл ПНЕВМОНИЯ и рассчитаем коэффициент корреляции УМЕР и числа лейкоцитов
Correlations
|
|
УМЕР |
white blood cell count |
УМЕР |
Pearson Correlation |
1,000 |
,062 |
|
Sig. (2-tailed) |
, |
,048 |
|
N |
1031 |
1031 |
white blood cell count |
Pearson Correlation |
,062 |
1,000 |
|
Sig. (2-tailed) |
,048 |
, |
|
N |
1031 |
1032 |
Получили слабую корреляционную связь.
Однако при изучении совместного распределения получаем следующее:
white blood cell count * УМЕР Crosstabulation
|
|
|
УМЕР |
|
Total |
|
|
|
,00 |
1,00 |
|
white blood cell count |
<4 |
Count |
30 |
27 |
57 |
|
|
% within white blood cell count |
52,6% |
47,4% |
100,0% |
|
4-9 |
Count |
302 |
6 |
308 |
|
|
% within white blood cell count |
98,1% |
1,9% |
100,0% |
|
9-25 |
Count |
554 |
38 |
592 |
|
|
% within white blood cell count |
93,6% |
6,4% |
100,0% |
|
>25 |
Count |
37 |
37 |
74 |
|
|
% within white blood cell count |
50,0% |
50,0% |
100,0% |
Total |
|
Count |
923 |
108 |
1031 |
|
|
% within white blood cell count |
89,5% |
10,5% |
100,0% |
То есть высокая летальность – при большом и малом числе лейкоцитов.
Аналогично приведенному выше создадим новую переменную «линеаризованные лейкоциты»

Для нее имеем следующее
Correlations
|
|
УМЕР |
white blood cell count |
LEJLIN |
УМЕР |
Pearson Correlation |
1,000 |
,062 |
,483 |
|
Sig. (2-tailed) |
, |
,048 |
,000 |
|
N |
1031 |
1031 |
1031 |
white blood cell count |
Pearson Correlation |
,062 |
1,000 |
,128 |
|
Sig. (2-tailed) |
,048 |
, |
,000 |
|
N |
1031 |
1032 |
1032 |
LEJLIN |
Pearson Correlation |
,483 |
,128 |
1,000 |
|
Sig. (2-tailed) |
,000 |
,000 |
, |
|
N |
1031 |
1032 |
1032 |
То есть после линеаризации связи число лейкоцитов стало достаточно сильным фактором с корреляцией около 0,5.
