§ 8. Дифференциальные уравнения второго порядка и выше, допускающие понижение порядка

1. Уравнения вида

Общее решение этого уравнения получают, произведя n последовательных интегрирований. При каждом таком интегрировании будет появляться новая произвольная постоянная.

Будем использовать то, что

Пример 8.1. Найти общее решение уравнения

Решение.

Проинтегрируем последовательно 4 раза

Пример 8.2. , , , Ответ.

2. Уравнения вида 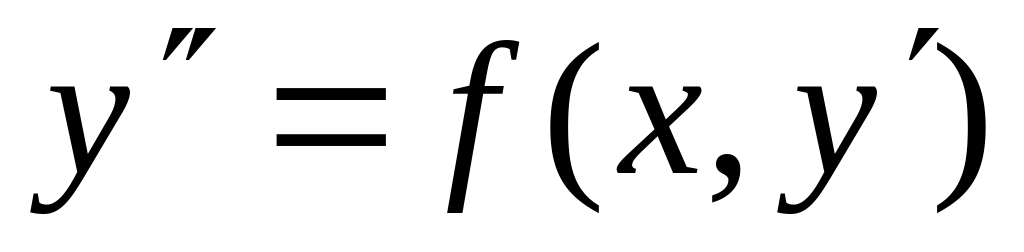, не содержащее явно искомой функции у.

Рассмотрим уравнение – д.у. второго порядка. Положим , где z=z(x), тогда . Подставим в исходное уравнение и получим – д.у. первого порядка. Проинтегрируем это уравнение и получим его общее решение

Пример 8.3. Найти частное решение уравнения , удовлетворяющее начальным условиям , .

Решение. Имеем д.у. второго порядка, не содержащее явно у. , .

,

– д.у. первого порядка с разделяющимися переменными

, , , ,

,

– общее решение.

– частное решение.

Пример 8.4. Ответ:

3. Уравнения вида 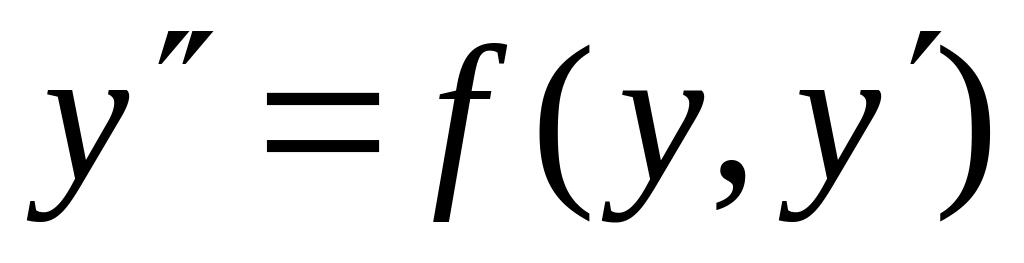, не содержащее явно независимой переменной х.

Положим , где z=z(у), тогда .

Пример 8.5. Найти частное решение д.у. , если , .

Решение. ,

, ,

, , , ,

, , ,

– общее решение.

Рассмотрим начальные условия , . Тогда – частное решение.

§ 9. Линейные однородные дифференциальные уравнения

Опр. Уравнение вида

(1),

линейное относительно неизвестной функции у и ее производных , называется линейным дифференциальным уравнением n-го порядка.

Функции a₁(x), …, a_n(x), f(x) – заданные функции от х или постоянные. Будем предполагать, что эти функции непрерывны в рассматриваемой области.

Функция f(x) называется правой частью уравнения.

Если , то (1) называется линейным неоднородным д.у. или уравнением с правой частью.

Если , то (1) примет вид

и называется линейным однородным д.у. или уравнением без правой части.

Свойства линейного однородного уравнения (на примере однородного уравнения второго порядка)

(2), где a₁=a₁(x), a₂=a₂(x)

Теорема 1. Если у₁(х), у₂(х) – частные решения уравнения (2), то их линейная комбинация также является решением этого уравнения при любых значениях постоянных с₁ и с₂.

Доказать самостоятельно.

Указание: подставить функцию и ее первую и второю производные в уравнение (2) и прийти к тождеству.

Опр. Две функции (два решения) у₁ и у₂ называются линейно независимыми на интервале (а;b), если равенство имеет место лишь при .

Функции у₁ и у₂ называются линейно зависимыми на (а;b), если существуют постоянные и , не обращающиеся одновременно в нуль и такие, что равенство справедливо

Замечание. Функции у₁ и у₂ линейно независимы, если , и линейно зависимы, если .

Пример 9.1.

,

у₁ и у₂ линейно независимы.

Пример 9.2.

,

у₁ и у₂ линейно зависимы.

Вопрос о том, будут ли у₁(х) и у₂(х) линейно зависимы или линейно независимы, можно решить с помощью определителя Вронского

– определить Вронского.

Теорема 2. Для того чтобы два частных решения линейного однородного уравнения второго порядка (2) были линейно независимы на (а;b) необходимо и достаточно, чтобы их определитель Вронского был отличен от нуля на этом интервале.

Без доказательства.

Теорема 3. (О структуре общего решения линейного однородного уравнения второго порядка) Если у₁(х) и у₂(х) – линейно независимые частные решения уравнения (2), то функция

(3),

где с₁ и с₂ – произвольные постоянные, является общим решением линейного однородного уравнения (2).

Доказательство.

Согласно определению общего решения следует доказать:

1) функция (3) является решением (2) при любых значениях постоянных с₁ и с₂. Выполняется согласно теореме 1;

2) каковы бы ни были начальные условия , произвольные постоянные с₁ и с₂ можно подобрать единственным образом так, чтобы соответствующее частное решение удовлетворяло этим начальным условиям. Подставим начальные условия в (3) и получим

, где с₁ и с₂ – неизвестные числа, х₀, у₀, – заданы.

Определитель системы по теореме 2. Значит, система имеет единственное решение, т.е. с₁ и с₂ подбираются единственным образом.