
- •Глава V. Дифференциальные уравнения
- •§ 1. Основные понятия и определения
- •§ 2. Дифференциальные уравнения первого порядка
- •§ 3. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •§ 4. Однородные дифференциальные уравнения первого порядка
- •§ 5. Линейные дифференциальные уравнения первого порядка
- •§ 6. Уравнение Бернулли
- •§ 7. Дифференциальные уравнения высших порядков. Общие понятия.
- •§ 8. Дифференциальные уравнения второго порядка и выше, допускающие понижение порядка
- •§ 9. Линейные однородные дифференциальные уравнения
- •§ 10. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •§ 11. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Глава V. Дифференциальные уравнения
§ 1. Основные понятия и определения
При изучении различных явлений часто не удается найти закон, связывающий величины, характеризующий это явление. Однако можно установить зависимость между этими величинами и их производными.
Опр. Дифференциальным
уравнением называется уравнение,
связывающее независимую переменную х,
искомую функцию y=y(x)
и ее производные
![]() ,
,
![]() ,
…
,
…
![]() ,
то есть соотношение вида
,
то есть соотношение вида
![]() (1).
(1).
Опр. Порядком дифференциального уравнения называется высший из порядков входящих в это уравнение производных.
Примеры:
 – д.у. первого порядка;
– д.у. первого порядка; – д.у. второго порядка;
– д.у. второго порядка;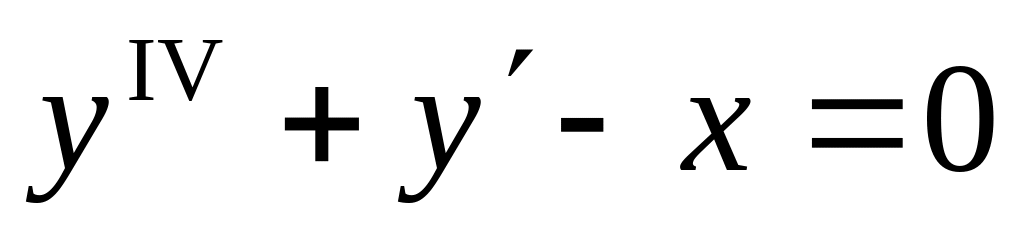 – д.у. четвертого порядка.
– д.у. четвертого порядка.
Опр. Решением дифференциального уравнения (1) называется n раз дифференцируемая функция, которая при подстановке в это уравнение обращает его в тождество.
Рассмотрим задачи, приводящие к (обыкновенным) дифференциальным уравнениям.
Задача 1.1. Радиоактивный распад.
Экспериментально установлено, что скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. М0 – начальное количество вещества. Найти зависимость между количеством нераспавшегося вещества М и временем t.
Решение.
Скорость радиоактивного распада равна
![]() ,
то есть производной от количества
вещества М по времени t.
,
то есть производной от количества
вещества М по времени t.
По условию:
![]() ,
где k – коэффициент
пропорциональности.
,
где k – коэффициент
пропорциональности.
«–», так как с возрастанием t количество вещества М уменьшается.
![]()
![]()
![]() ,
проинтегрируем и получим
,
проинтегрируем и получим
![]()
![]()
![]() .
При t=0:
.
При t=0:
![]()
![]()
![]() .
.
Коэффициент k можно
определить экспериментально. Например,
для М0=1ч определили, что
![]() .
Значит, процесс распада протекает по
формуле
.
Значит, процесс распада протекает по
формуле
![]() .
Через 10 мин количество нераспавшегося
вещества равно
.
Через 10 мин количество нераспавшегося
вещества равно
![]() г.
г.
Задача 1.2. Найти уравнение семейства кривых, зная, что угловой коэффициент касательной в каждой точке любой кривой семейства равен отношению ординаты этой точки к ее абсциссе, взятому с противоположным знаком.
Решение.
y=y(x) – уравнение кривой
![]() ,
,
![]()
![]() – д.у. первого порядка
– д.у. первого порядка
![]()
![]()
![]()
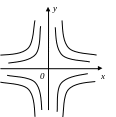
![]() – решение д.у., семейство гипербол.
– решение д.у., семейство гипербол.
Проверим, что
–
решение.
![]() ,
,
![]() – тождество.
– тождество.
Задача нахождения решения д.у. называется интегрированием дифференциального уравнения, а график решения д.у. – интегральной кривой.
§ 2. Дифференциальные уравнения первого порядка
В общем случае д.у. Iго порядка имеет вид
![]() .
.
Если его можно разрешить относительно , то получим
![]() –
д.у., разрешенное относительно
.
–
д.у., разрешенное относительно
.
Д.у. первого порядка также можно записать
в виде
![]() или
или
![]() .
.
Теорема Коши. Теорема о существовании и единственности решения д.у. .
Если в уравнении
(1)
функция
![]() и ее частная производная
и ее частная производная
![]() непрерывны в некоторой области D
плоскости Оху, содержащей точку
(х0;у0), то найдется
интервал
непрерывны в некоторой области D
плоскости Оху, содержащей точку
(х0;у0), то найдется
интервал
![]() ,
на котором существует единственное
решение y=y(x)
этого уравнения, удовлетворяющее условию
y(x0)=
y0 (2).
,
на котором существует единственное
решение y=y(x)
этого уравнения, удовлетворяющее условию
y(x0)=
y0 (2).
Без доказательства.
Задача нахождения решения д.у. (1), удовлетворяющего условию (2) называется задачей Коши, а условие y(x0)= y0 называют начальным условием.
Другие записи начального условия: y=
y0 при
х=х0;
![]() .
.
Опр. Функция y=y(x,c), где с – произвольная постоянная, называется общим решением д.у. (1) в области D, если:
она является решением этого уравнения при любом значении с;
какова бы ни была точка (х0;у0), лежащая внутри D, существует единственное значение с=с0 такое, что решение y=y(x,c0) удовлетворяет начальному условию y(x0)= y0.
Опр. Частным решением д.у. (1) называется решение y=y(x,c0), которое получается из общего решения y=y(x,c) при конкретном с=с0.
Геометрическая иллюстрация
Общему решению соответствует семейство интегральных кривых (задача 1.2. – семейство гипербол).
Отыскание частного решения по начальному условию y(x0)=y0 геометрически означает, что из семейства интегральных кривых выбираем ту, которая проходит через точку (х0;у0). Согласно теореме Коши через каждую точку, в которой функции и непрерывны, проходит единственная интегральная кривая.
Точки (х;у), в которых не выполняются условия теоремы, называются особыми точками д.у. В этих точках и терпят разрыв. Через особую точку либо не проходит ни одна интегральная кривая, либо проходит несколько.
Рассмотрим задачу 1.2.
– д.у.; – общее решение (семейство гипербол).
Найдем частное решение, удовлетворяющее начальному условию у(2)=1.
![]() с=2
с=2
![]() – частное решение.
– частное решение.
Общему решению соответствует семейство гипербол. Частному решению – одна кривая этого семейства, проходящая через точку (2;1).

Замечание. Часто общее
решение д.у. можно получить только в
неявном виде, то есть в виде
![]() .
Это равенство называют общим
интегралом д.у. Если с=с0,
то получим частный интеграл.
.
Это равенство называют общим
интегралом д.у. Если с=с0,
то получим частный интеграл.
