Приложение а (справочное) Программы расчета критических скоростей вала

Пример 1 - Определение критических скоростей цилиндрических валов в зависимости от жесткости левой опоры

Схема исходного вала изображена на рисунке:

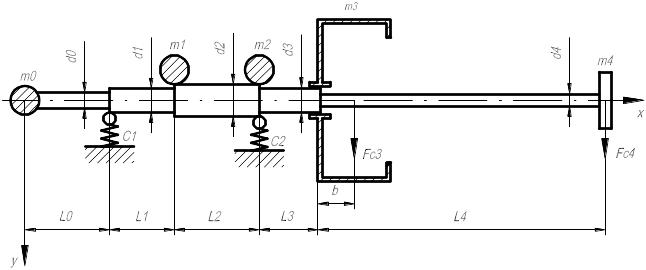
Исходные данные:

Номера участка вала Диаметр Длина Масса

Коэффициенты жесткости упругих опор, Н*м^-1:

левой ..........................................

правой .........................................

Расстояние от центра тяжести до точки закрепления массы

ротора, м .......................................

Модуль упругости, Па .............................

Начальное значение критической скорости, сек^-1 ...

Количество рассчитываемых скоростей...............

Плотность материала, кг*м^-3 ......................

Разность между полярным и осевым моментами инерции масс, кг*м^{2 :}

m₃ .............................................

m₄ .............................................

Начало массива....................................

Погрешность вычислений ...........................

продолжение приложения А

Описание функций частот для всех участков вала

Осевой момент инерции сечения вала

Аргумент для функций частот

Нормальные фундаментальные

решения уравнения

(y_i)^''''-K_i⁴*y_i=0 (векторы значений функций частот) S(_i), T(_i), U(_i), V(_i) соответственно

Описание уравнений упругой линии и первых трёх производных для каждого участка вала.

продолжение приложения А

Нулевой участок вала

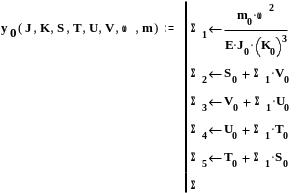
Первый участок вала

продолжение приложения А

Второй участок вала

продолжение приложения А

Третий участок вала

продолжение приложения А

Четвёртый участок вала

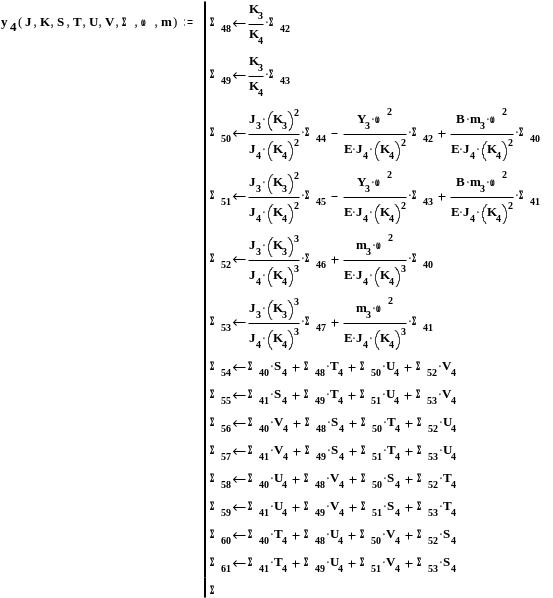
продолжение приложения А

Описание определителя системы двух линейных алгебраических уравнений относительно начальных параметров

Описание вспомогательной процедуры поиска корней уравнения

продолжение приложения А

Методом последовательного приближения с шагом находим приближённые значения первых критических скоростей при фиксированных параметрах рассчитываемого вала:

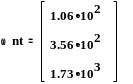
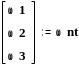
Находим точные значения критических скоростей, используя в качестве начальных условий приближённые значения этих скоростей

Первая критическая скорость

Вторая критическая скорость

Третья критическая скорость

Замечание:

Если функция Find() не может определить точное значение корня kr (то есть (kr2,d,l,m,c1,c2)) то, следует изменить шаг приращения значения критической скорости и/или использовать функцию Minerr() вместо Find(). Однако следует иметь в виду, что Find() возвращает точное значение.

Определяем зависимость критической скорости от жесткости левой опоры.

Задаем вектор жесткости левой опоры:

Замечание:

В зависимости от поставленной задачи необходимо задать 10 значений жесткости левой опоры, но не ниже Н*м^-1

Рассчитываем критические скорости в каждой точке:

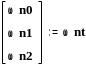
продолжение приложения А

продолжение приложения А

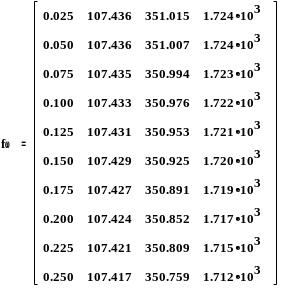
Формируем матрицу f результатов расчета зависимости критической скорости от жесткости левой опоры:

Результаты расчета записываем в файл kritikc1.prn

продолжение приложения А

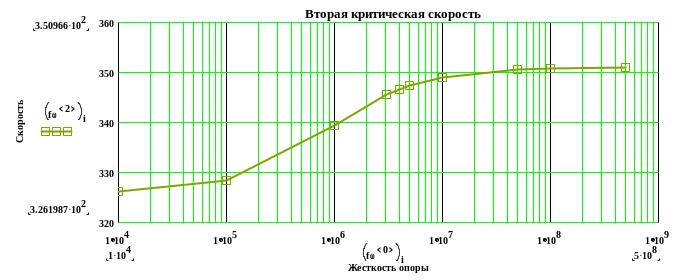
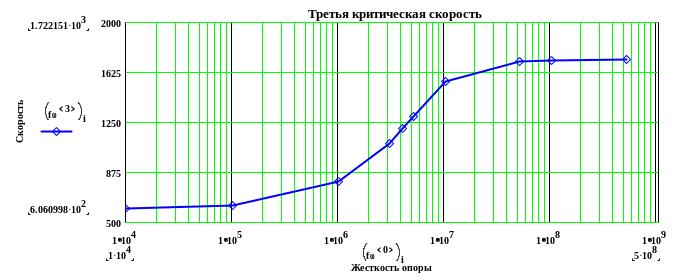
Строим графики зависимостей первых критических скоростей от жесткости левой опоры :

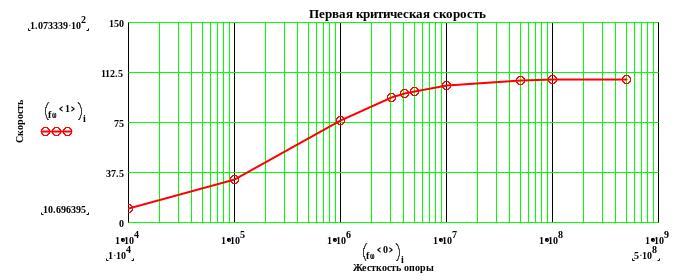
продолжение приложения А

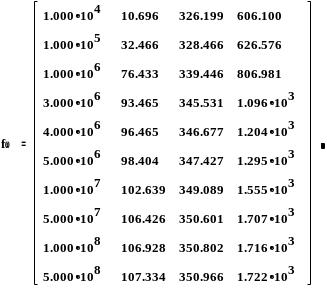
Матрица результатов расчета зависимости критической скорости от жесткости левой опоры:

продолжение приложения А

Пример 2 - Определение критических скоростей цилиндрических валов в зависимости от величины сосредоточенной массы выбранного участка вала

Схема исходного вала изображена на рисунке:

Исходные данные:

Номера участка вала Диаметр Длина Масса

Коэффициенты жесткости упругих опор, Н*м^-1:

левой ..........................................

правой .........................................

Расстояние от центра тяжести до точки закрепления массы

ротора, м .......................................

Модуль упругости, Па .............................

Начальное значение критической скорости, сек^-1 ...

Количество рассчитываемых скоростей...............

Плотность материала, кг*м^-3 ......................

Разность между полярным и осевым моментами инерции масс, кг*м^{2 :}

m₃ .............................................

m₄ .............................................

Начало массива....................................

Погрешность вычислений ...........................

продолжение приложения А

Описание функций частот для всех участков вала

Осевой момент инерции сечения вала

Аргумент для функций частот

Нормальные фундоментальные

решения уравнения

(y_i)^''''-K_i⁴*y_i=0 (векторы значений функций частот) S(_i), T(_i), U(_i), V(_i) соответственно

Описание уравнений упругой линии и первых трёх производных для каждого участка вала.

продолжение приложения А

Нулевой участок вала

Первый участок вала

продолжение приложения А

Второй участок вала

продолжение приложения А

Третий участок вала

продолжение приложения А

Четвёртый участок вала

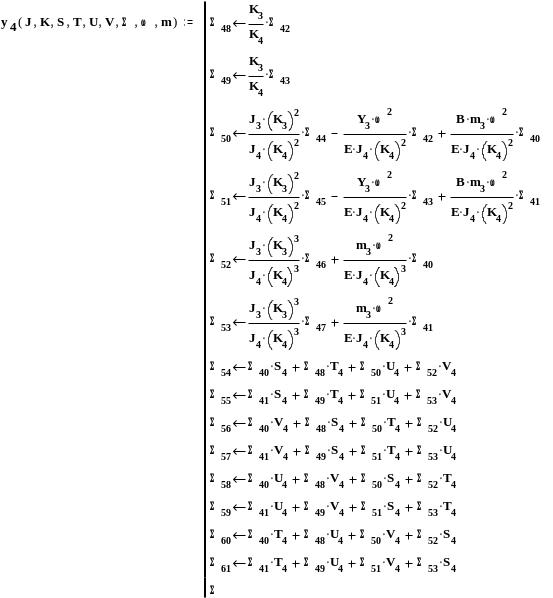
продолжение приложения А

Описание определителя системы двух линейных алгебраических уравнений относительно начальных параметров

Описание вспомогательных процедур поиска корней уравнения

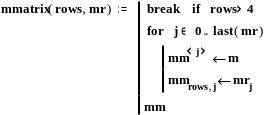
продолжение приложения А

Методом последовательного приближения с шагом

находим приближённые значения первых критических скоростей при фиксированных параметрах рассчитываемого вала:

Находим точные значения критических скоростей, используя в качестве начальных условий приближённые значения этих скоростей

Первая критическая скорость

Вторая критическая скорость

Третья критическая скорость

Замечание:

Если функция Find() не может определить точное значение корня kr (то есть (kr2,d,l,m,c1,c2)) то, следует изменить шаг приращения значения критической скорости и/или использовать функцию Minerr() вместо Find(). Однако следует иметь в виду, что Find() возвращает точное значение.

Определяем зависимость критической скорости от массы выбранного участка.

Задаем номер участка вала:

Задаем вектор масс выбранного участка вала

Замечание:

В зависимости от поставленной задачи необходимо задать 10 значений масс указанного участка вала.

Рассчитываем критические скорости в каждой точке:

продолжение приложения А

продолжение приложения А

Формируем матрицу f результатов расчета зависимости критической скорости от массы участка вала:

Результаты расчета записываем в файл kritikd.prn

продолжение приложения А

Строим графики зависимостей первых критических скоростей от массы участка вала:

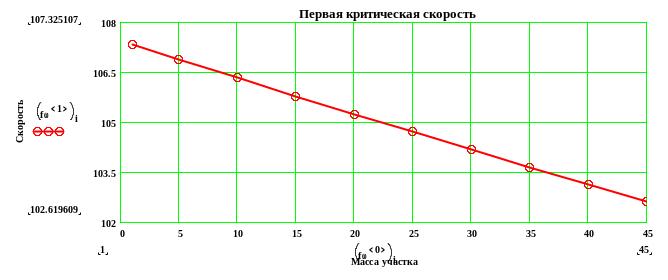
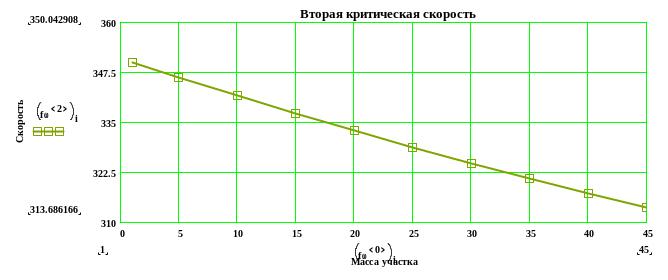
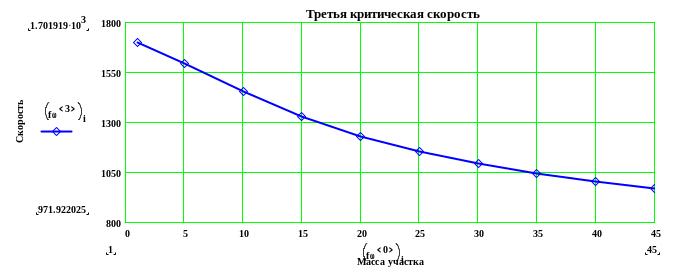
продолжение приложения А

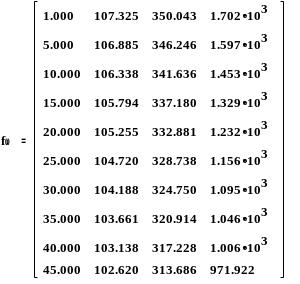
Матрица результатов расчета зависимости критической скорости от массы участка вала:

продолжение приложения А

Пример 3 - Определение критических скоростей цилиндрических валов в зависимости от диаметра выбранного участка вала

Схема исходного вала изображена на рисунке:

Исходные данные:

Номера участка вала Диаметр Длина Масса

Коэффициенты жесткости упругих опор, Н*м^-1:

левой ..........................................

правой .........................................

Расстояние от центра тяжести до точки закрепления массы

ротора, м.........................................

Модуль упругости, Па .............................

Начальное значение критической скорости, сек^-1 ...

Количество рассчитываемых скоростей...............

Плотность материала, кг*м^-3 ......................

Разность между полярным и осевым моментами инерции масс, кг*м^{2 :}

m₃ .............................................

m₄ .............................................

Начало массива....................................

Погрешность вычислений ...........................

продолжение приложения А

Описание функций частот для всех участков вала

Осевой момент инерции сечения вала

Аргумент для функций частот

Нормальные фундоментальные

решения уравнения

(y_i)^''''-K_i⁴*y_i=0 (векторы значений функций частот) S(_i), T(_i), U(_i), V(_i) соответственно

Описание уравнений упругой линии и первых трёх производных для каждого участка вала.

продолжение приложения А

Нулевой участок вала

Первый участок вала

продолжение приложения А

Второй участок вала

продолжение приложения А

Третий участок вала

продолжение приложения А

Четвёртый участок вала

продолжение приложения А

Описание определителя системы двух линейных алгебраических уравнений относительно начальных параметров

Описание вспомогательных процедур поиска корней уравнения

продолжение приложения А

Методом последовательного приближения с шагом

находим приближённые значения первых критических скоростей при фиксированных параметрах рассчитываемого вала:

Находим точные значения критических скоростей, используя в качестве начальных условий приближённые значения этих скоростей

Первая критическая скорость

Вторая критическая скорость

Третья критическая скорость

Замечание:

Если функция Find() не может определить точное значение корня kr (то есть (kr2,d,l,m,c1,c2)) то, следует изменить шаг приращения значения критической скорости и/или использовать функцию Minerr() вместо Find(). Однако следует иметь в виду, что Find() возвращает точное значение.

Определяем зависимость критической скорости от диаметра, выбранного участка.

Задаем номер участка вала:

Задаем вектор диаметров выбранного участка вала

Замечание:

В зависимости от поставленной задачи необходимо задать 10 значений диаметров указанного участка вала.

Рассчитываем критические скорости в каждой точке:

продолжение приложения А

продолжение приложения А

Формируем матрицу f результатов расчета зависимости критической скорости от диаметра участка вала:

Результаты расчета записываем в файл kritikd.prn

продолжение приложения А

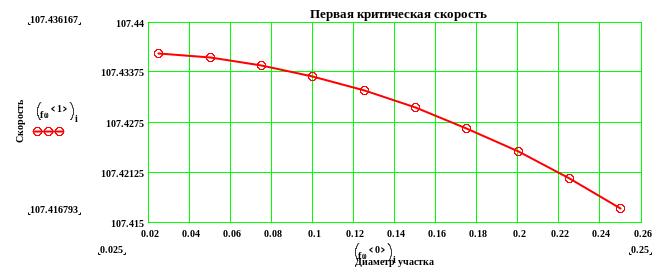
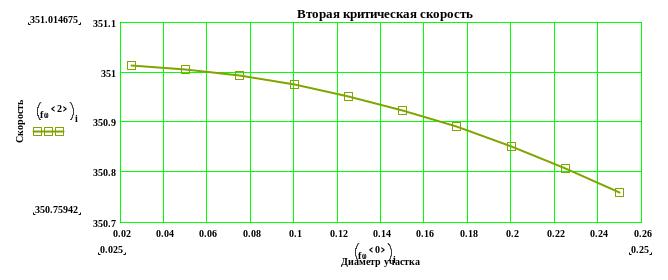
Строим графики зависимостей первых критических скоростей от диаметра участка вала:

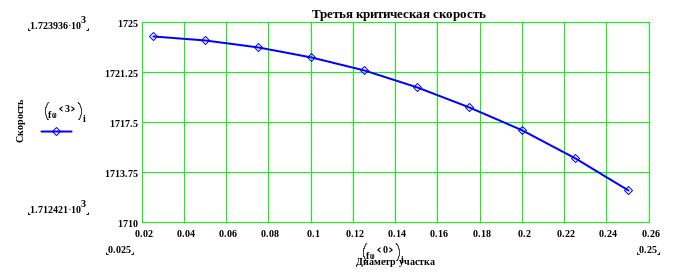
продолжение приложения А

Матрица результатов расчета зависимости критической скорости от диаметра участка вала: