Нулевой участок

Уравнение упругой линии нулевого участка вала, согласно выражению (2.3), записывается

Первые три производные

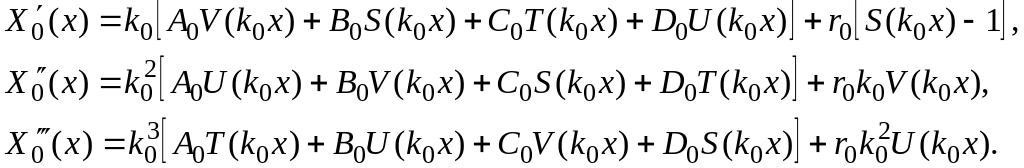
Краевые условия на левом конце вала

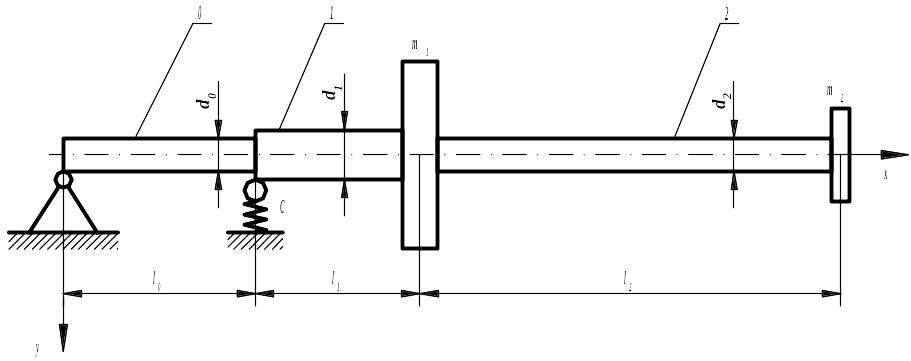
Рисунок 9 – Расчетная схема вала

Тогда и при имеем:

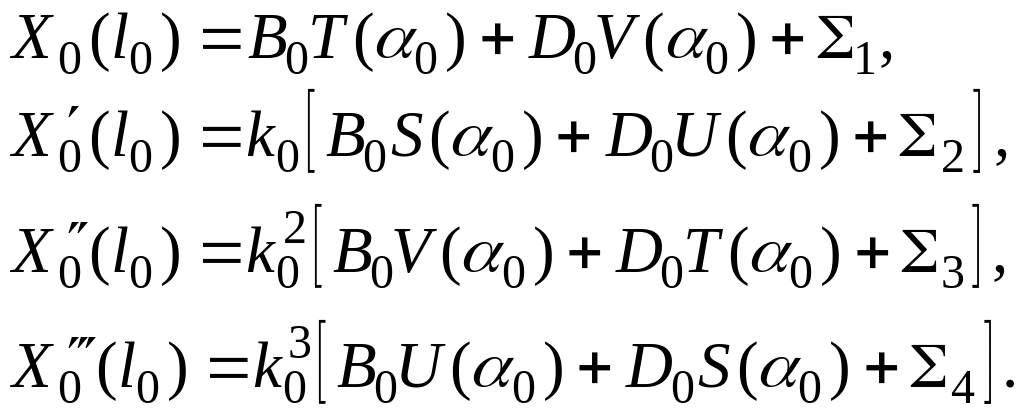(2.4)

где

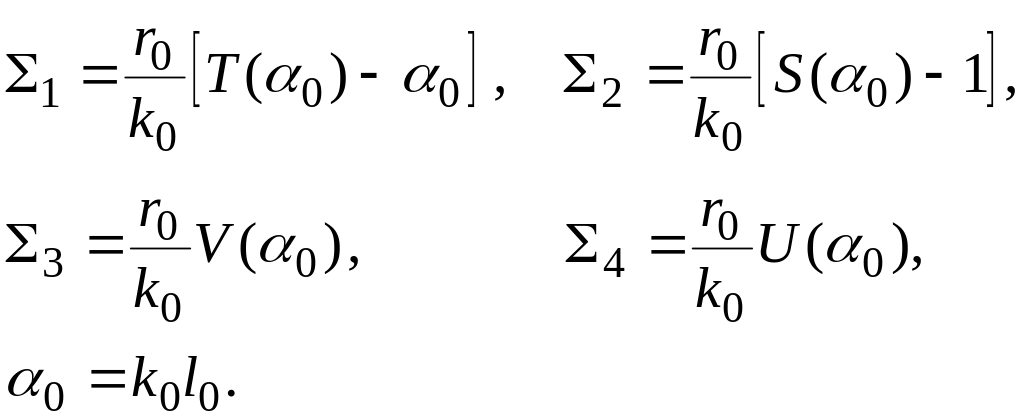
Первый участок

Уравнение упругой линии первого участка и его первые три производные:

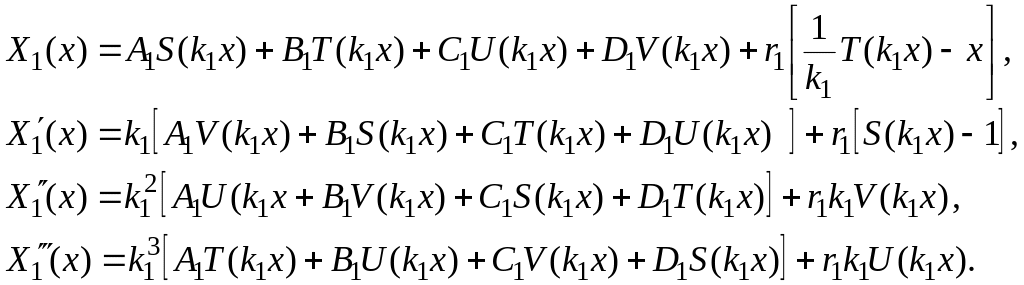(2.5)

Условия сопряжения нулевого и первого участков вала:

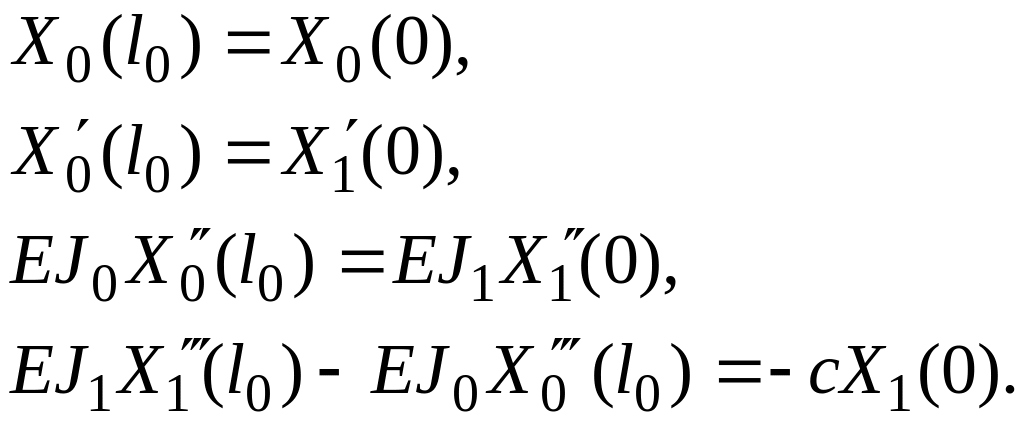(2.6)

Подставляя выражения (2.5) при и (2.4) в условия сопряжения (2.6), найдем постоянные интегрирования первого участка вала:

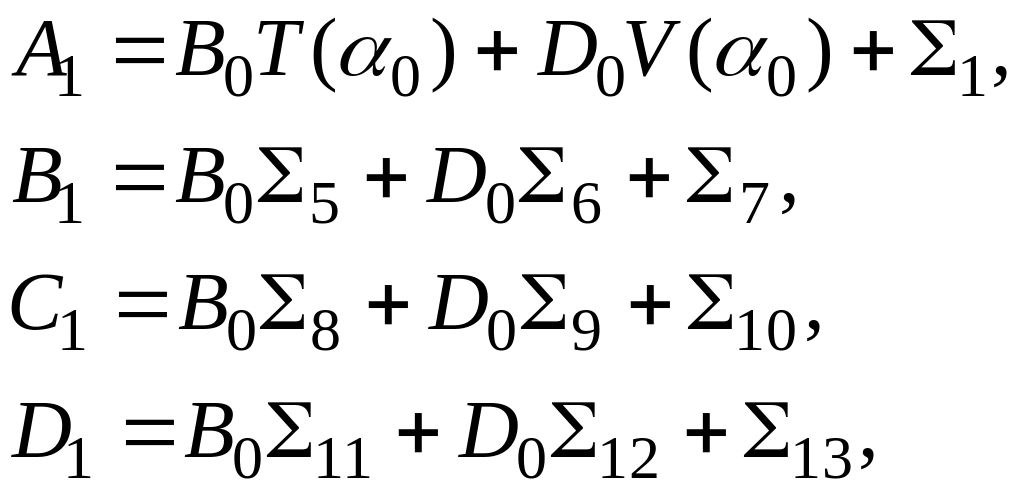(2.7)

где

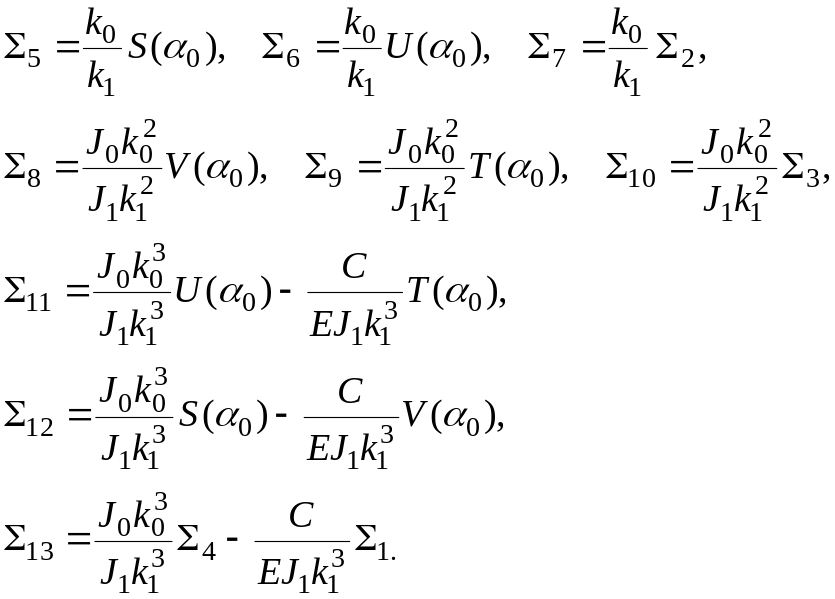
С учетом выражений (2.7) уравнение упругой линии первого участка вала и его первые три производные при запишутся:

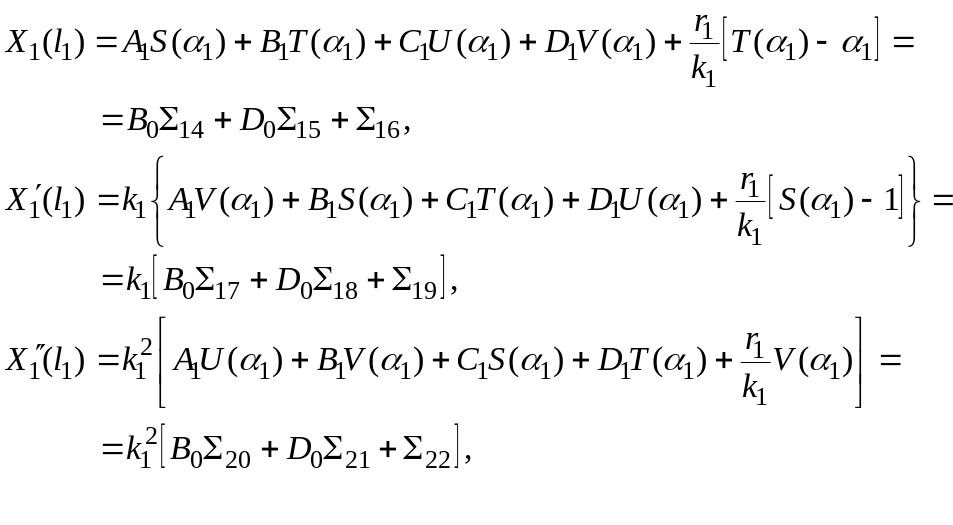(2.8)

Второй участок

Уравнение упругой линии второго участка вала и его первые три производные:

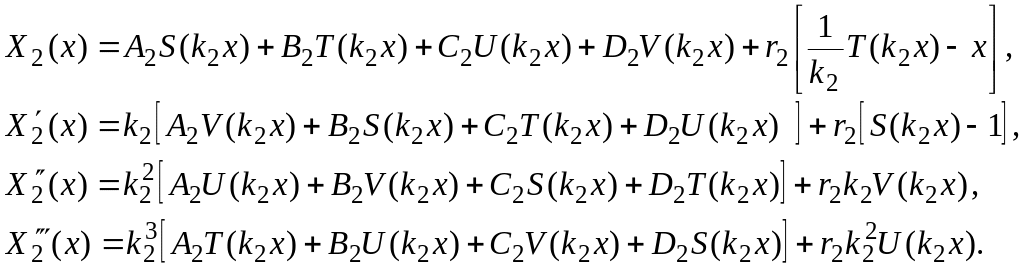(2.9)

Условия сопряжения первого и второго участков вала:

(2.10)

где эксцентриситет массы .

Подставляя выражения (2.9) при и (2.8) в условиях сопряжения (2.10), найдем постоянные интегрирования второго участка вала.

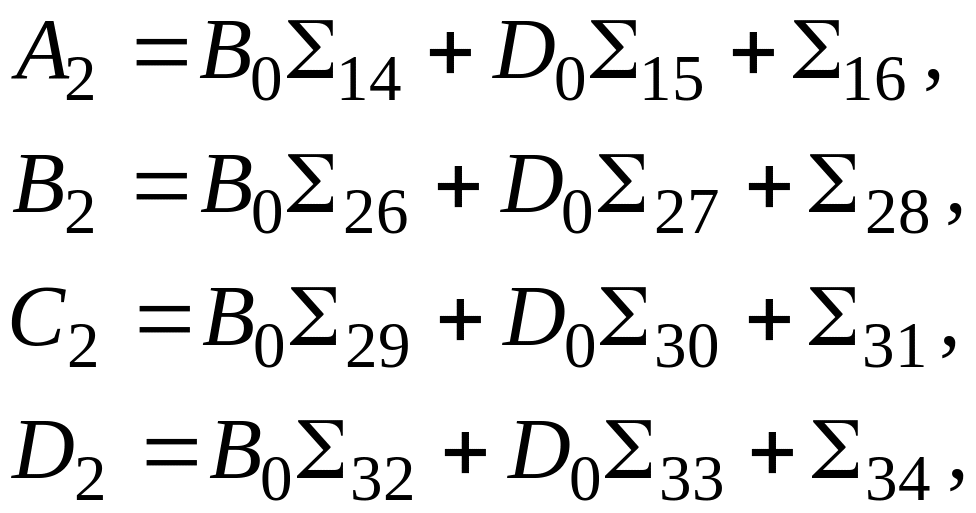(2.11)

где

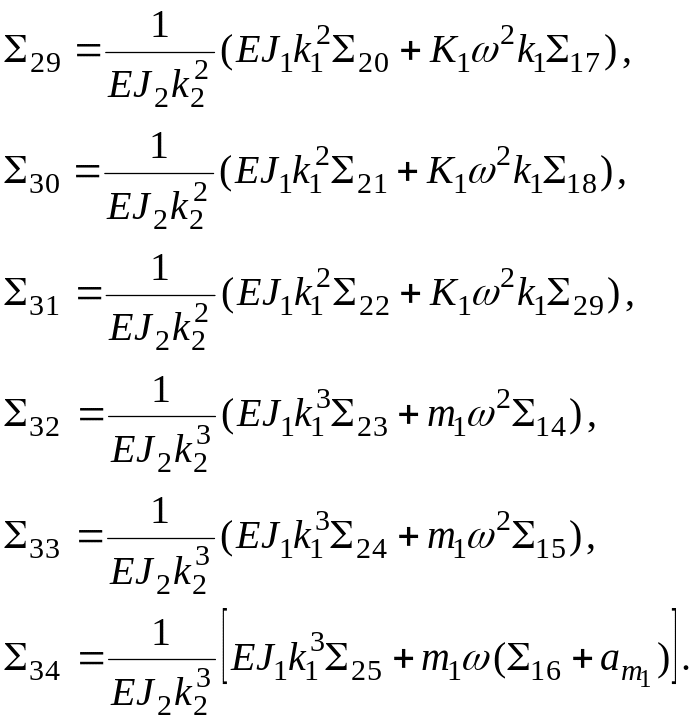
С учетом выражений (2.11) уравнение упругой линии второго участка вала и его первые три производные при запишутся:

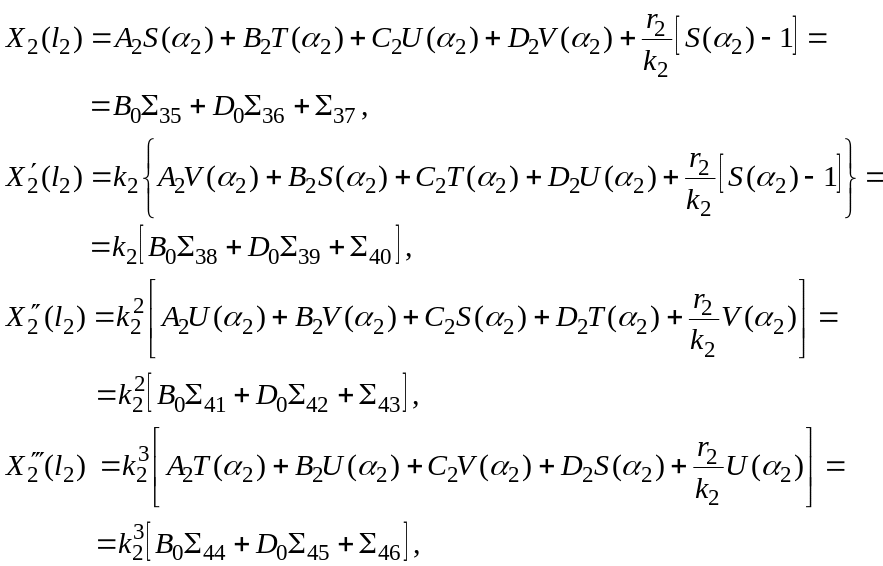
где

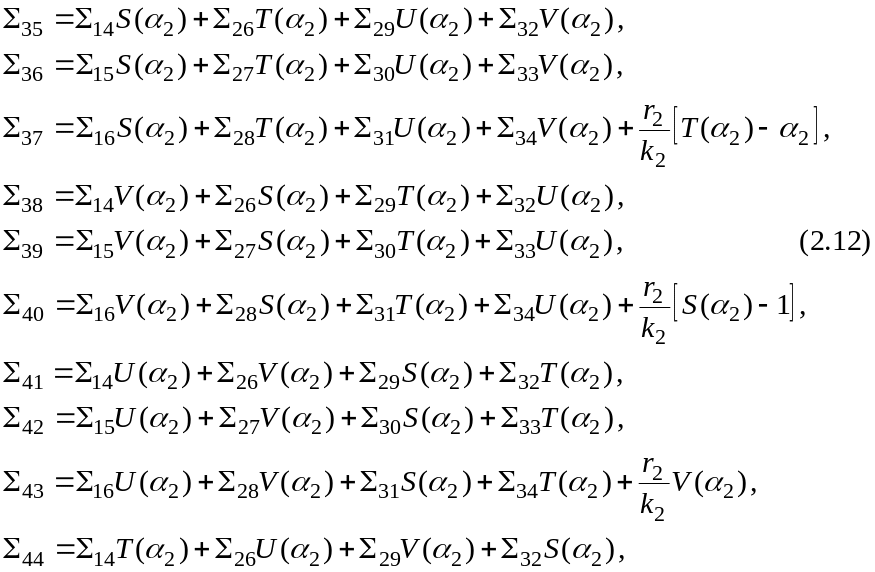
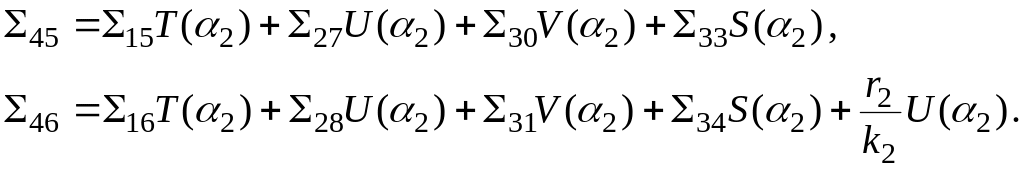
Краевые условия на правом конце вала:

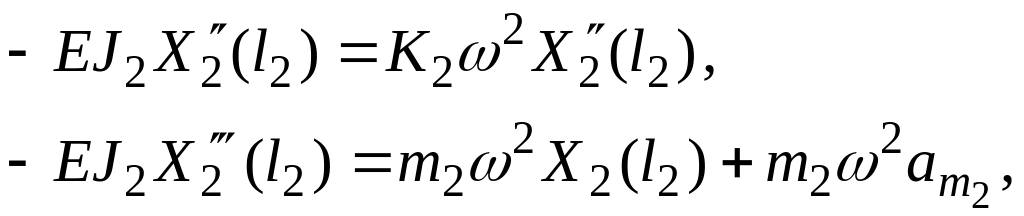(2.13)

где эксцентриситет массы .

Подставляя выражения (2.12) в условия сопряжения (2.13), получим два неоднородных алгебраических уравнения с неизвестными :

(2.14)

где

Из уравнений (2.14) определяем постоянные интегрирования нулевого участка :

Прогибы вала в сечениях запишутся:

(2.15)

.

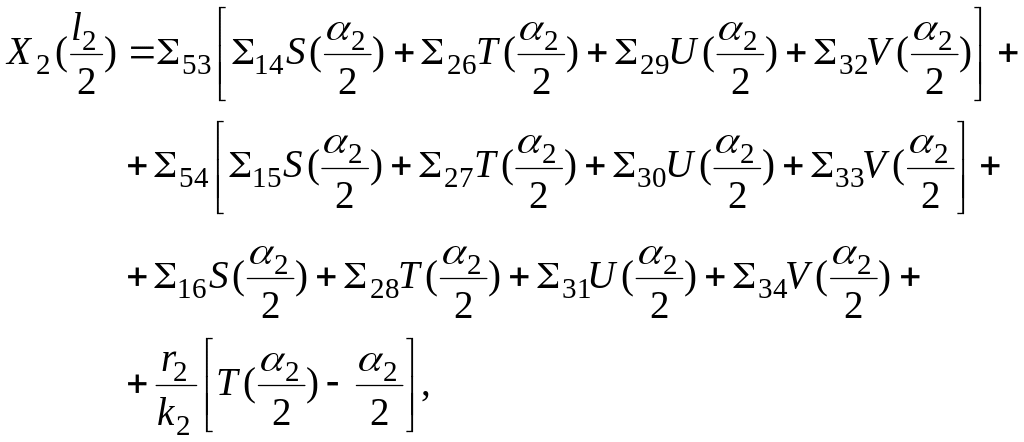
Реакции опор в сечениях вала соответственно

(2.16)

Изгибающие моменты в сечениях вала :

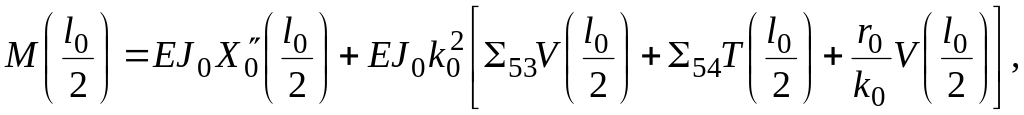
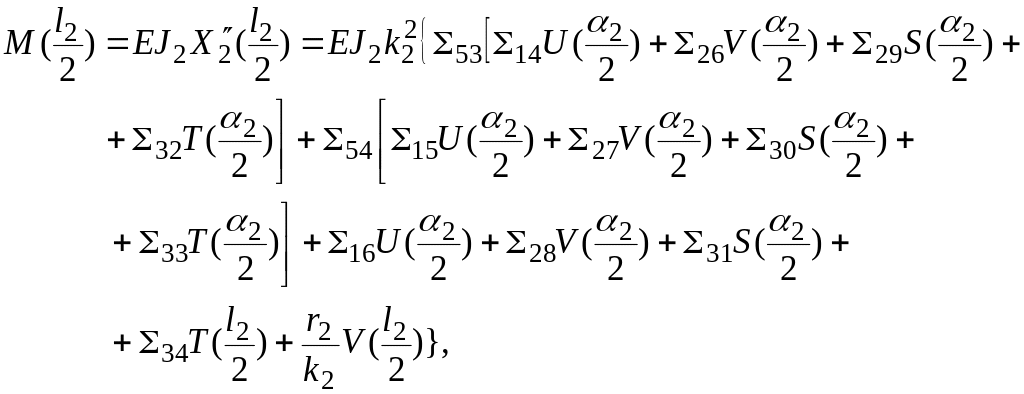(2.17)

Таким образом, с помощью полученных зависимостей (2.15) – (2.17) могут быть определены форма упругой линии вала, реакции опор и найдены опасные сечения вала при любой скорости его вращения.

2.2 Нестационарный режим вращения

Рассмотрение вынужденных изгибных колебаний вала при нестационарном режиме вращения позволяет решить следующие вопросы:

1) рассчитать резонансные амплитуды и определить необходимые зазоры между вращающимися и неподвижными деталями машин (для гибких валов). Знание максимальных амплитуд колебаний вала имеет первостепенную важность в тех случаях, когда по технологическим или другим соображениям зазоры между вращающимися и неподвижными деталями машины должны быть минимальными.

2) оценить реакции опор и напряжения, развивающиеся в опасных сечениях вала при переходе через резонанс, что особенно важно при многократных пусках и остановках вала.

2.2.1 Краткий обзор состояния вопроса

Исследование поведения механических систем при нестационарном переходе через резонансное или критическое состояние развивается, в основном, по следующим направлениям:

- линейная постановка задачи при заранее предписанном законе изменения частоты возмущающей силы;

- нелинейная постановка задачи при заранее предписанном законе изменения частоты возмущающей силы;

- источник энергии и колебательная система рассматриваются как единая, автономная система, в которой имеет место обратная связь. В этом случае частота возмущающей силы зависит от источника энергии, свойств колебательной системы и её поведения в процессе колебаний.

Наиболее полно рассмотрены нестационарные колебания линейных механических систем. Линейные системы являются наиболее простыми моделями реальных объектов и позволяют применить линейную теорию. Нелинейные системы – это широкий класс систем, которые наиболее правильно моделируют реальные объекты. Теория нелинейных колебаний использует очень сложный математический аппарат, поэтому для исследования характера колебаний нелинейных систем обычно прибегают к различным приемам линеаризации. Однако при исследовании существенно нелинейных систем, когда линеаризация принципиально невозможна, применяются специальные методы решения: численное интегрирование, использование аппарата специальных функций, моделирующие устройства, ЭВМ.

Следует отметить, что задачи о нестационарных колебаниях даже в самых простейших случаях отличаются большой математической сложностью. Так, если вращающийся вал может быть приведен к линейной системе с одной степенью свободы (в предположении, что источник энергии обладает достаточно большой мощностью), то решение задачи сводится к интегрированию дифференциального уравнения

(2.18)

где		-	линейное перемещение;
		-	коэффициент, характеризующий затухание;
		-	частота свободных колебаний;
		-	амплитуда возмущающей силы, отнесенная к единице мас-
сы системы;

здесь скорость изменения частоты ,

Интеграл дифференциального уравнения (2.18):

(2.19)

где

Прохождение через резонанс линейной системы с одной степенью свободы посвящены работы Н.Г. Горчакова, А.М. Каца, Б.Г. Коренева, А.Д. Мышкиса, Я.Г. Пановко, А.П. Филиппова и других авторов.

Имеется целый ряд работ, относящихся к анализу переходных процессов в линейных системах с конкретной механической интерпретацией, в частности, большое внимание уделяется изучению колебаний валов в нестационарном режиме. Это работы В.А. Гробова, А.А. Гусарова, П.Л. Капицы, И.Ш. Неймана, Н.А. Пикулева, О.Н. Романива, А.А. Смелкова, К.Т. Шаталова, И.С. Шейнина и других авторов.

В работе Ф.М. Диментберга /3/ исследуется вопрос о соотношении переменной и «постоянной» (медленно изменяющейся во времени) составляющих прогиба вала с диском посередине на жестких и упруго-податливых опорах. Выясняется роль податливости опор. Автор получает решения без учета и с учетом внешнего вязкого трения, представленные через интегралы Френеля действительного аргумента.

Дальнейшим развитием вопроса о нестационарных колебаниях механических систем явилась работа Е.Г. Голоскокова и А.П. Филиппова /1/, в которых подробно рассматривается прохождение через резонанс системы с одной степенью свободы в режимах разгона и выбега при действии возмущающих сил различного характера, с учетом и без учета сил трения. Полученные решения распространяются на случай систем с конечным числом степеней свободы и с распределенными параметрами.

Наряду с развитием теории линейных колебаний за последнее время значительное развитие получили приближенные методы исследования нестационарных колебаний в нелинейных системах, основывающиеся на асимптотических методах нелинейной механики.

Следует особо подчеркнуть важность исследований Ю.А. Митропольского по теории нестационарных колебаний нелинейных систем, обобщенных в монографии /7/. Развивая идеи асимптотических методов нелинейной механики, созданных Н.М. Крыловым и Н.Н. Боголюбовым, автор разработал достаточно общий метод исследования нестационарных колебаний в нелинейных системах с медленно изменяющимися параметрами.

Идеи асимптотических методов используются в работах В.А. Гробова /2/, Е.Г. Голоскокова и А.П. Филиппова /1/ и других авторов.

В.О. Кононенко /4/ положил начало новому разделу в исследованиях нестационарных колебаний механических систем с ограниченным возбуждением. Автором излагаются основные особенности поведения систем с ограниченным возбуждением, исследуются энергетические соотношения, вносимые связностью с двигателем. Для изучения взаимодействия колебательных систем с источником энергии широко использовалось электромоделирование.

Поведение систем с ограниченным возбуждением в дальнейшем рассматривалось в работах Э.А. Аграновской, Е.Г. Голоскокова, С.С. Кораблева, Л.А. Растригина. А.П. Субача и других авторов.

2.2.2 Решение линейной задачи

Анализ конструкций машин и аппаратов, применяемых в химической промышленности, показывает, что во многих случаях вращающиеся валы могут быть рассмотрены как линейные системы с распределенными параметрами.

Наиболее подробно решение такой задачи приведено в работе /17/ на примере разгона вала цетрифуги, расчетная схема которого приведена на рисунке 9.

Переход вала через критическую скорость рассматривается в предположении, что угловая скорость возрастает по заранее предписанному линейному закону , не зависящему от поперечных колебаний системы. Как известно, этот случай соответствует наличию в системе источника энергии, обладающего неограниченным запасом мощности. Характеристика упругой опоры принимается изотропной и линейной с коэффициентом жесткости . Силы внешнего трения принимаются пропорциональными скорости перемещения вала, силы внутреннего трения не учитываются. После изготовления и сборки вал имеет изогнутость Между опорами изогнутость вала изменяется по синусоидальному закону, а на консоли изогнутость по линейному, то есть

Массы имеют остаточную неуравновешенность, характеризуемую соответственно эксцентриситетами Предполагается, что векторы эксцентриситетов распределенных и сосредоточенных масс на каждом участке вала лежат в одной плоскости и направлены в одну сторону, то есть рассматривается худший возможный случай.

Неподвижные оси координат - , подвижные - ; точка центр вала, точка центр тяжести сечения вала (рисунок 10).

Проекции прогиба вала на неподвижные оси координат отыскиваются в виде:

(2.20)

если отношение их массы к массе ротора не превышает 0,005. В противном случае их масса приводится к массе ротора;

где			- функции времени;
			- собственная функция -го участка вала -й частоты.

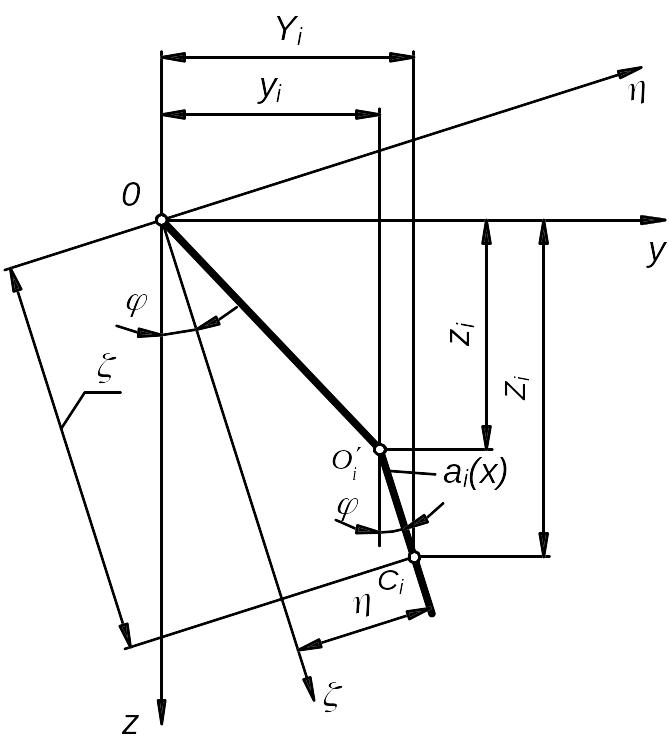
Рисунок 10 – Схема прогиба вращающегося вала в сечении

1) Определение собственных функций

Дифференциальное уравнение для определения собственных функций вала имеет вид, аналогичный уравнению (1.1) /5, 17/.

(2.21)

где здесь собственная частота -го порядка.

В случае многоопорного вала переменного сечения собственные функции участков вала целесообразно находить методом начальных параметров, что позволяет получить довольно простые, удобные для практических расчетов выражения.

Собственные функции вала:

- на нулевом участке

- на первом участке

- на втором участке

Рассматривая, как и прежде, краевые условия на концах вала, а также условия сопряжения между участками, получим следующие выражения для собственных функций вала:

Нулевой участок

(2.22)

(2.23)

где , здесь

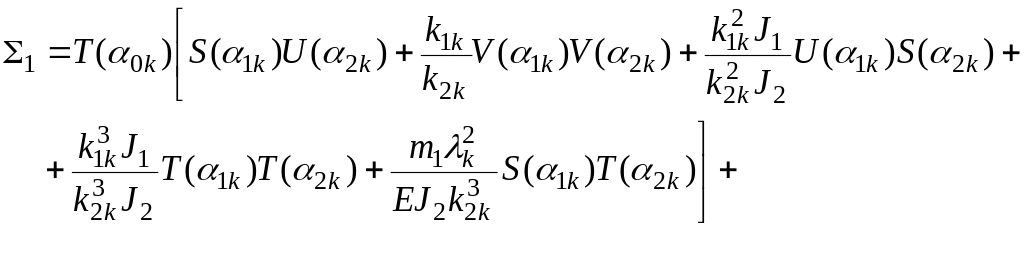
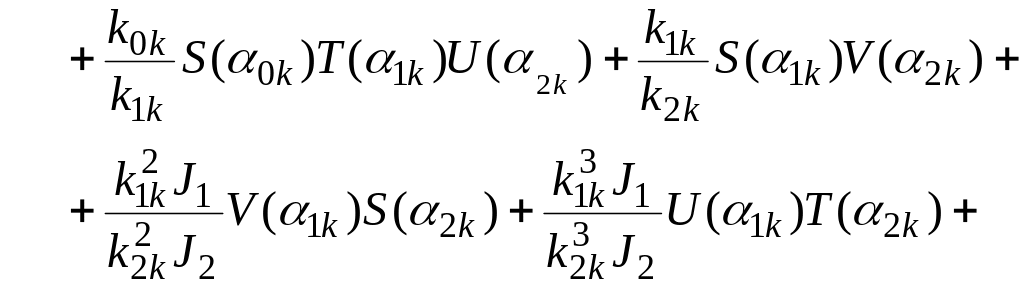
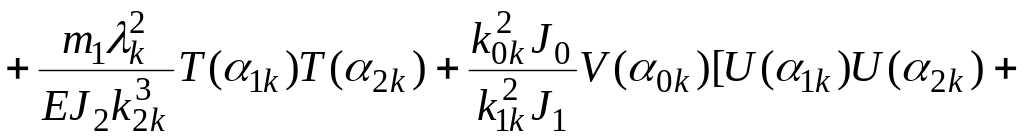
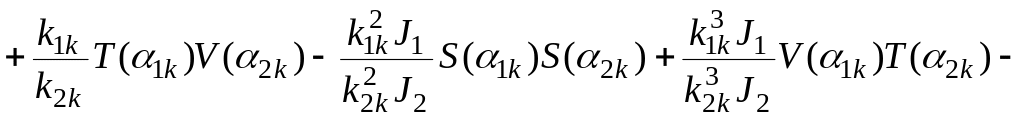
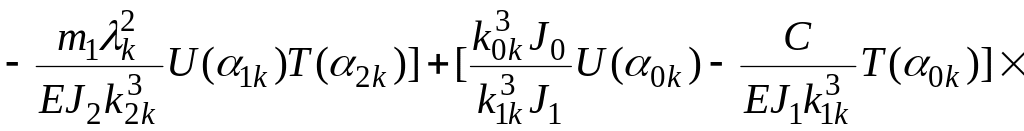
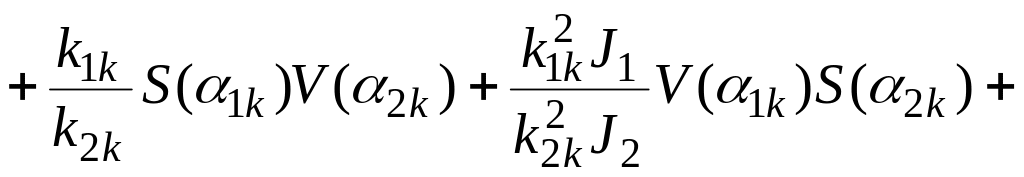
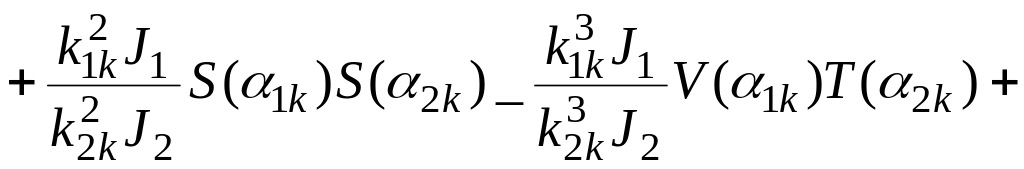
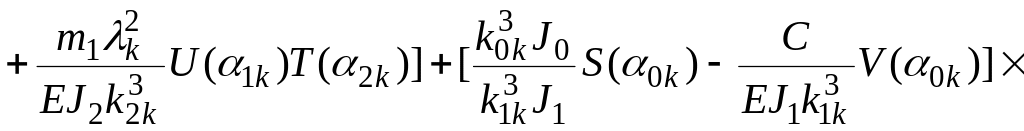
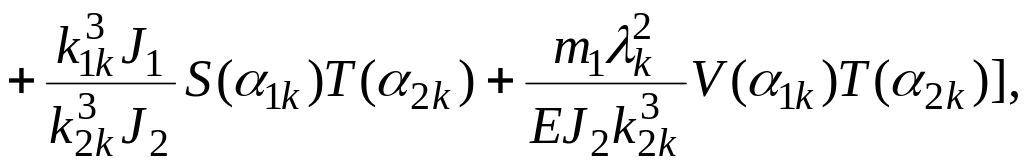
где

Первый участок

(2.24)

(2.25)

где

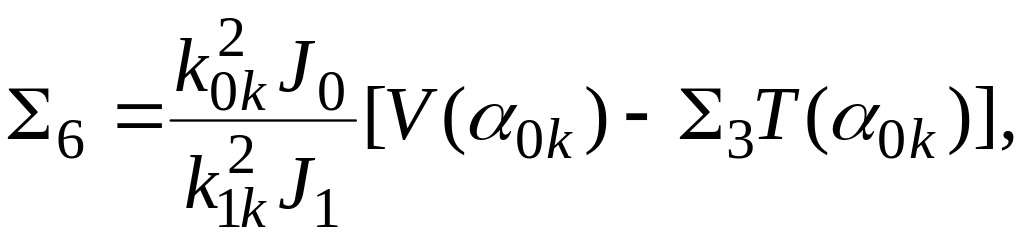
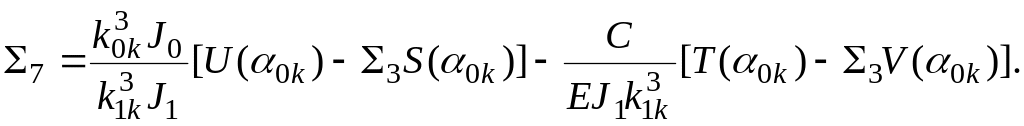
Второй участок

(2.26)

(2.27)

где

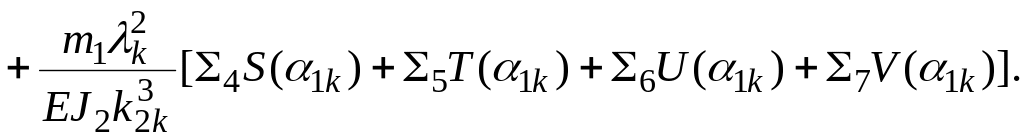
В выражения собственных функций входит неизвестная постоянная интегрирования нулевого участка. При дальнейших выкладках эта величина сокращается и не препятствует получению решения в замкнутом виде.

2) Определение функций времени

Для определения функций используются уравнения Лагранжа

(2.28)

кинетическая энергия вращающегося вала;

потенциальная энергия изогнутого вала и деформированной упругой опоры;

обобщенные силы внешнего трения, отнесенные к координатам ;

обобщенные силы внутреннего трения, отнесенные к тем же координатам.

Кинетическая энергия вращающегося вала /1, 3, 17/:

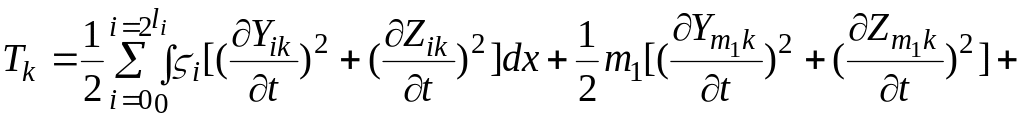
(2.29)

где проекции перемещения центра тяжести произвольного сечения -го участка вала на неподвижные оси координат ,

проекции перемещений центров тяжести сосредоточенных масс на неподвижные оси .

полярные моменты инерции масс

Потенциальная энергия изогнутого вала и деформированной упругой опоры /5,17/:

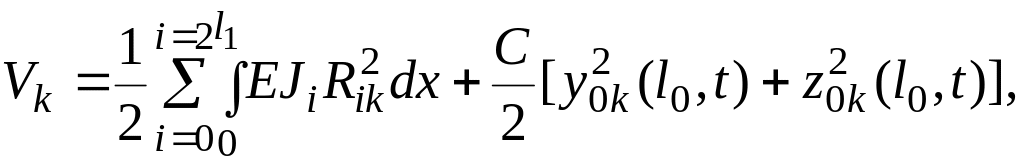(2.30)

где - кривизна упругой линии вала,

При определении обобщенных сил трения считается, что внутреннее трение не способствует ограничению амплитуд при переходе вала через критические скорости /1/.

Механическое объяснение этого факта сводится к тому, что в резонансной зоне упругая линия вала, изогнутого центробежными силами от неуравновешенности распределенных и сосредоточенных масс, вращается вокруг линии опор и при этом не происходит вращения вала «внутри» упругой линии, нет перемен знаков напряжений и, следовательно, внутреннее трение практически отсутствует, то есть можно принять

Силы внешнего трения возникают главным образом в опорах и принимаются пропорциональными скорости перемещения вала. В этом случае проекции внешних сил на координатные оси записываются соответственно в следующем виде /5, 17/:

в жесткой опоре

в упругой опоре

где и коэффициенты пропорциональности, определяемые опытным путем.

Тогда обобщенные силы внешнего трения с учетом выражений (2.20) будут:

(2.31)

Подставляя выражения (2.29) – (2.31) в уравнения Лагранжа (2.28), получим два дифференциальных уравнения:

(2.32)

где

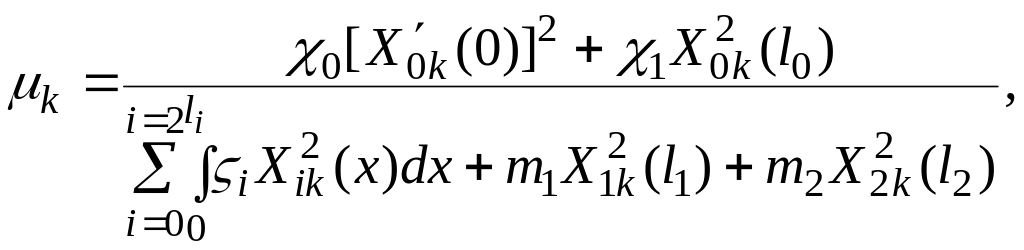
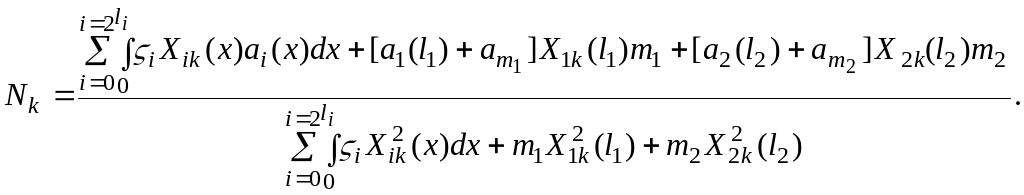
Подставляя значения собственных функций в выражения для и , после интегрирования и ряда преобразований получим:

,

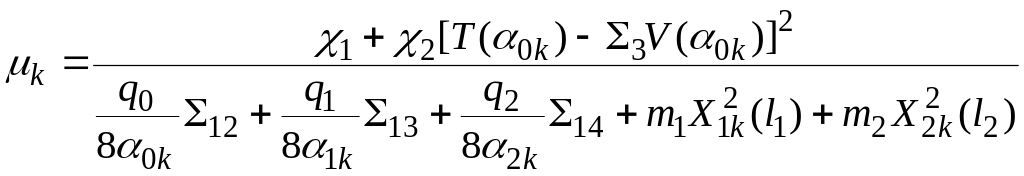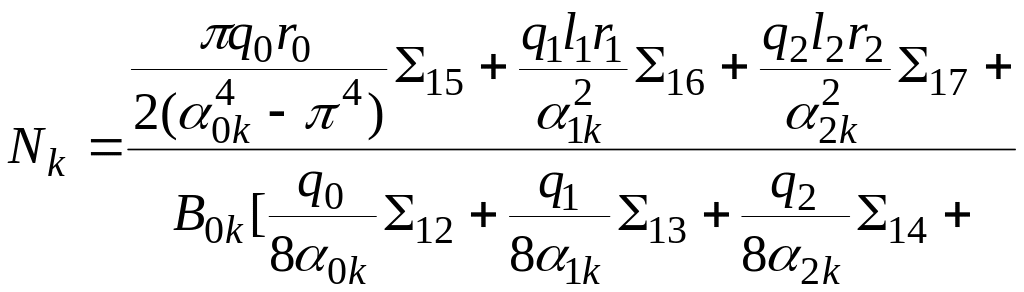
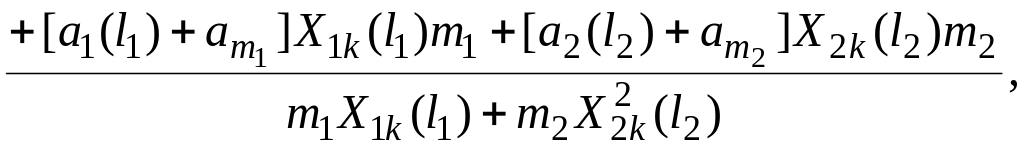
где распределенные массы нулевого, первого и второго участков вала,

Интегралы уравнений (2.32) при нулевых начальных условиях запишутся соответственно:

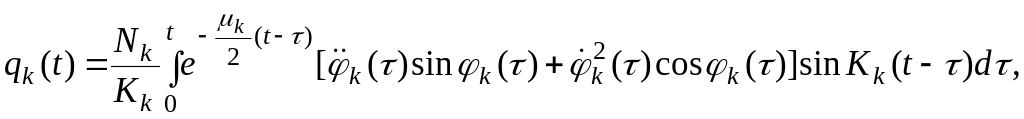(2.33)

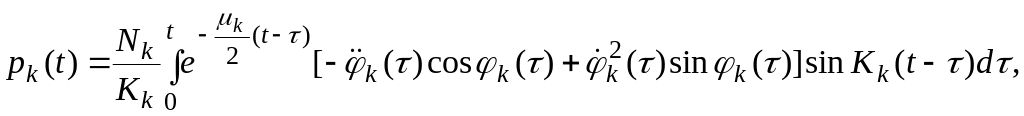(2.34)

где

Интегрируя по частям уравнения (2.33) и (2.34), получим для следующие выражения:

(2.35)

(2.36)

где

здесь

Интегралы могут быть выражены через интегралы Френеля или интегралы Жильбера комплексного аргумента. Однако более простым является решение через интегралы вероятностей комплексного аргумента /1/. Для этого делается переход к интегрированию в комплексной области. Показательные функции принимаются в качестве аналитического продолжения функций на плоскость комплексного переменного, то есть

(2.37)

где

Далее в выражениях (2.37) по тождествам Эйлера представляются в виде показательных функций. Множители, не зависящие от выносятся за знак интеграла и вместо вводятся новые переменные /1,17/:

для интегралов

для интегралов

Для интеграла имеем следующее решение /1/:

(2.38)

где

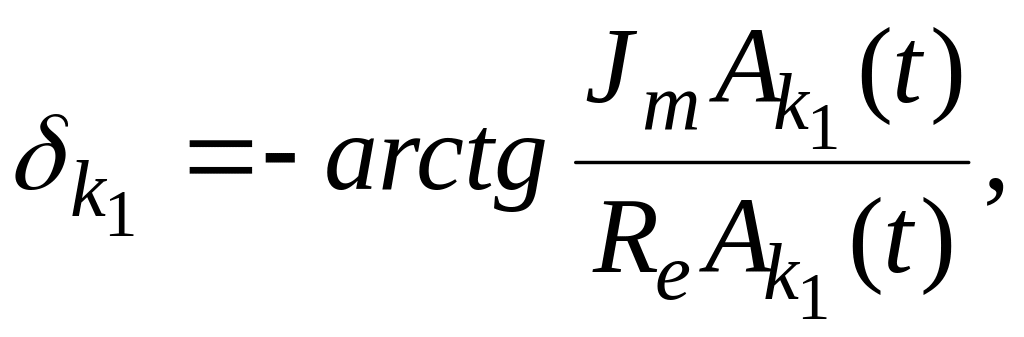
здесь интегралы вероятностей комплексного аргумента, для которых имеются подробные таблицы /18/;

значения при

соответственно действительная и мнимая части .

Аналогично для интегралов имеем решения /17/:

(2.39)

где

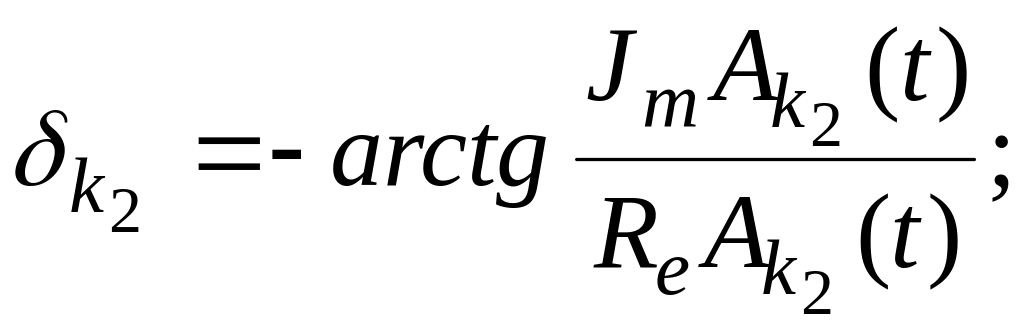
(2.40)

где

Здесь значения при ,

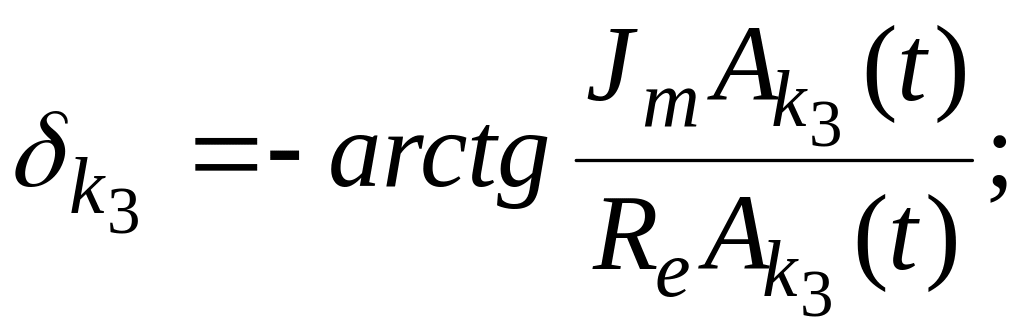
(2.41)

где

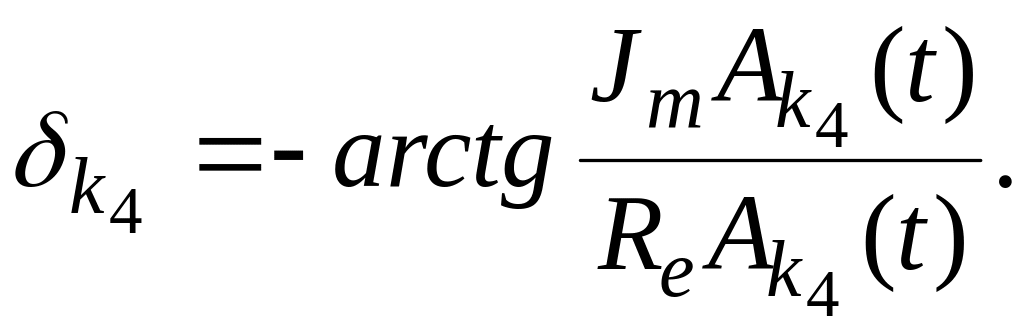
Подставляя выражения (2.38) и (2.39) в (2.35), а выражения (2.40) и (2.41) в (2.36), получим окончательно

Результирующий прогиб на -ом участке вала определяется по формуле

Изгибающие моменты и поперечные силы на -ом участке вала, если на нем не приложены внешние моменты и силы, в проекциях на координатные оси и определяются соответственно из следующих выражений:

где

Результирующие изгибающие моменты и поперечные силы на -ом участке вала

Полученные расчетные зависимости позволяют исследовать переход вала через критические скорости любого порядка с учетом влияния как высших, так и низших гармоник.

Например, для вала, представленного на рисунке 9, при переходе через первую критическую скорость с учетом влияния второй гармоники прогибы в сечениях вала определяются из следующих выражений:

где функции времени, определяемые из условия, что вал с формой колебаний, соответствующей второй гармонике, проходит через первую критическую скорость;

собственные функции соответственно нулевого, первого и второго участков вала, соответствующие первой гармонике;

собственные функции нулевого, первого и второго участков вала, соответствующие второй гармонике.

Аналогично могут быть найдены величины изгибающих моментов и поперечных сил в любом сечении.

Пример. Рассчитать нестационарный режим изгибных колебаний вала центрифуги, расчетная схема которого приведена на рисунке 9.

Исходные данные:

При переходе через первую критическую скорость с ускорением получены с помощью ЭВМ максимальные значения прогибов и изгибающих моментов в пяти сечениях вала, а также реакции опор ( в жесткой шарнирной, в упруго-податливой), приведенные в таблице 2.

Таблица 2 – Результаты расчетов

Вычисляемые параметры	Координата х сечения вала
	0
Прогиб	0	0,160	0,350	0,765	1,655	2,656
Изгибающий момент	0	107,1	214,8	85,2	26,6	0
Реакция опоры	790	-	1400	-	-	-

Момент резонанса

Литература

1 Голоскоков Е.Г., Филиппов А.П. Нестационарные колебания механических систем. – Киев: Наукова думка, 1966. – 336 с.

2 Гробов В.А. Асимптотические методы расчета изгибных колебаний валов турбомашин. – М.: Изд-во АН СССР, 1961. – 166 с.

3 Диментберг Ф.М. Изгибные колебания вращающихся валов. – М.: Изд-во АН СССР, 1959. – 247 с.

4 Кононенко В.О. Колебательные системы с ограниченным возбуждением. – М.: Наука, 1964. – 254 с.

5 Кущуль М.Я. Автоколебания роторов. – М.: Изд-во АН СССР, 1963. – 167 с.

6 Маслов Г.С. Расчеты колебаний валов. Справочник. – М.: Машиностроение, 1980. – 151 с.

7 Митропольский Ю.А. Проблемы асимптотической теории нестационарных колебаний. – М.: Наука, 1964. – 431 с.

8 Пановко Я.Г. Основы прикладной теории упругих колебаний. – М.: Машиностроение, 1967. – 316 с.

9 Филиппов А.П. Колебания деформируемых систем. – М.: Машиностроение, 1970. – 736 с.

10 Крылов А.Н. Об определении критических скоростей вращающегося вала. – Л.: Изд-во АН СССР, 1932. – 31 с.

11 Щеглов А.А. К вопросу определения критических скоростей вала переменного сечения. – В.кн.: Расчеты на прочность. – М.: Машгиз, 1960, вып. 5, с. 273-299.

12 Фаддеева В.Н., Гавурин М.К. Таблицы функций Бесселя целых номеров. –М. – Л.: Гостехтеориздат, 1950. – 439 с.

13 Соколовский В.И., Митрофанов Ю.А., Борисов Б.Р. О применении метода обобщенного анализа к исследованию критических скоростей валов. – Изв. вузов. Машиностроение, 1969, №8, с. 51-55.

14 Соколовский В.И., Митрофанов Ю.А., Борисов Б.Р. О выборе жесткости упругой опоры консольных валов центрифуг. – В.кн. : Проблемы машиностроения. Челябинск, Изд-во ЧПИ, 1973, с.3-14.

15 Борисов Б.Р., Митрофанов Ю.А. К определению критических скоростей и амплитуд колебаний валов центрифуг. – В кн.: Исследования кинематики и динамики машин. Свердловск, Изд-во УПИ, 1970, с. 129-135.

16 Ананьев И.В. Справочник по расчету собственных колебаний упругих систем. – М. – Л.: Гостехиздат, 1946. – 223 с.

17 Борисов Б.Р., Митрофанов Ю.А., Пенцов В.М. Исследование вынужденных изгибных колебаний вала центрифуги при нестационарном режиме вращения. – В.кн.: Динамика и прочность машин. – Харьков, Изд-во ХГУ, 1973, с. 15-51.

18 Фаддеева В.Н., Терентьев Н.М. Таблицы значений интеграла вероятностей от комплексного аргумента. – М.: Гостехиздат, 1954. – 268 с.