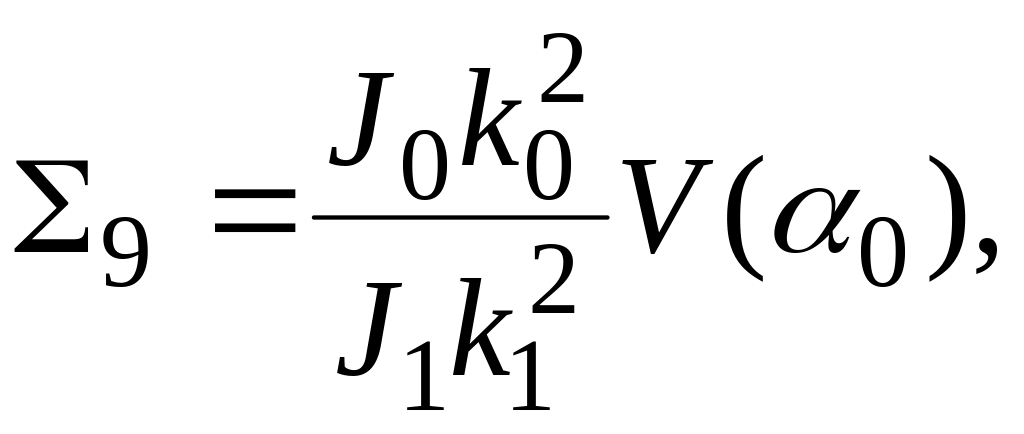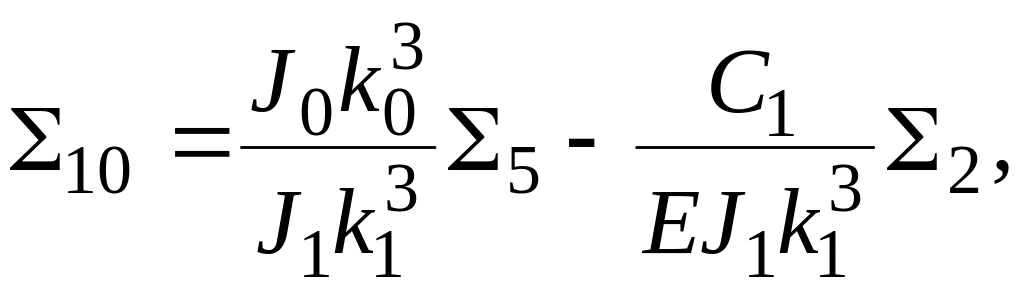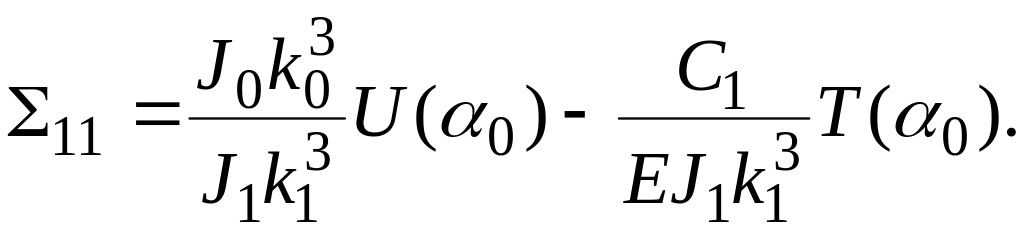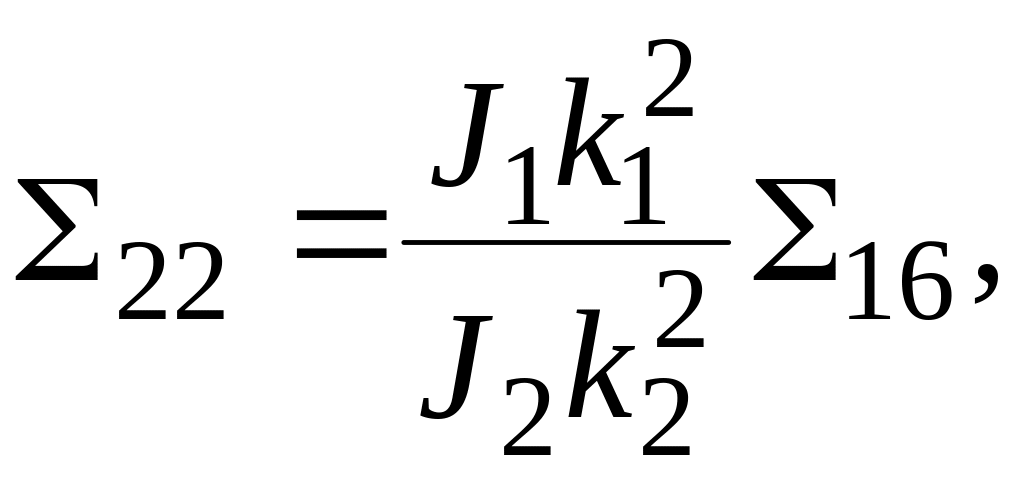Федеральное агентство по образованию

Северская государственная технологическая академия

Томский политехнический университет

__________________________________________________________________

Ю.А.Митрофанов

В.М.Замятин

ИЗГИБНЫЕ КОЛЕБАНИЯ

БЫСТРОВРАЩАЮЩИХСЯ ВАЛОВ

Допущено Учебно-методическим объединением вузов по образованию в области автоматизированного машиностроения (УМО АМ) в качестве учебника для студентов высших учебных заведений, обучающихся по направлению подготовки дипломированных специалистов «Конструкторско-технологическое обеспечение машиностроительных производств»

Томск 2006

УДК 621.824.534

Митрофанов Ю.А., Замятин В.М. Изгибные колебания быстровращающихся валов (для машиностроительных специальностей): Учебник. – Томск: 2006. -103 с.

В учебнике приведены методы расчета изгибных колебаний валов в стационарном и нестационарном режимах вращения. Дается вывод расчетных зависимостей для ряда схем, наиболее часто применяемых в машиностроении.

Учебник подготовлен на кафедрах технической механики и графики Северской государственной технологической академии и теоретической и прикладной механики Томского политехнического университета и предназначен для студентов машиностроительных специальностей, а также для специальности 170500 «Машины и аппараты химических производств».

Печатается по постановлению Редакционно-издательского Совета Томского политехнического университета

Рецензенты:

В.А. Архипов – профессор, доктор физико-математических наук, Томский государственный университет.

С.П. Курдынко – главный механик Сибирского химического комбината, канд. технических наук.

Темплан 2006

©Северская государственная технологическая академия,

Томский политехнический университет, 2006

Введение

В отечественной промышленности широкое применение получили различные машины, аппараты, имеющие в основе своей конструкции быстровращающиеся валы: турбогенераторы, газовые и паровые турбины, реактивные двигатели и т.п.; в химической промышленности – центрифуги, сепараторы, мешалки, центробежные экстракторы, кристаллизаторы, центробежные погружные насосы. Применение высокооборотного оборудования позволяет значительно интенсифицировать многие производственные процессы и повысить их экономическую эффективность.

Рабочие скорости быстровращающихся валов, как правило, располагаются за первой, второй, а иногда и за пределами критических скоростей более высокого порядка. Это обстоятельство в значительной степени повышает уровень требований, предъявляемых к вопросам расчета и проектирования таких валов.

На современном этапе при разработке конструкции вращающегося вала особое внимание уделяется вопросам расчета его вынужденных изгибных колебаний, вызванных как неуравновешенностью самого вала, так и закрепленных на нем узлов и деталей.

В последние два-три десятилетия появилось большое количество работ, посвященных теоретическому и экспериментальному решению вопросов колебаний валов. Это работы Е.Г.Голоскокова, А.П.Филиппова /1, 9/, В.А.Гробова /2/, Ф.М.Диментберга /3/, В.О.Кононенко /4/, М.Я.Кущуля /5/, Т.С.Маслова /6/, Ю.А.Митропольского /7/, Я.Г.Пановко /8/ и других авторов, которые явились крупным вкладом в развитие современной отечественной теории колебаний валов.

Рассмотрение изгибных колебаний валов в полном объеме – это достаточно сложная в теоретическом отношении и трудоемкая задача. Поэтому в инженерной практике в первую очередь решаются следующие вопросы:

1. определение критических скоростей вращающегося вала;

2) расчет стационарного режима вращения вала;

3) расчет нестационарного режима вращения (разгона и выбега) вала.

Решение этих вопросов позволяет правильно выбрать диапазон рабочих скоростей вала, определить как в стационарном, так и в переходном режимах форму упругой линии вала, выбрать необходимые зазоры между вращающимися и неподвижными узлами машины, найти реакции опор и рассчитать вал на прочность с учетом динамического нагружения.

Если решение данных вопросов является недостаточным для разработки конструкции вала и всей машины в целом, то рассматриваются и другие, более сложные, вопросы: устойчивость вращения вала, возможность возникновения автоколебаний и т.д.

При дальнейшем изложении основные сведения из теории колебаний механических систем предполагаются известными.

1 Определение критических скоростей валов

При вращении точки оси вала описывают окружности в направлении вращения или в противоположном направлении. В первом случае ось вала совершает прямую прецессию, во втором – обратную.

Различают критические скорости прямой и обратной прецессии вала. Теоретические и экспериментальные исследования [3, 6] показывают, что колебательное движение, вызываемое неуравновешенность вала или закрепленных на нем сосредоточенных масс, обычно приводит к прямой прецессии.

Критической скоростью прямой прецессии вала без учета гироскопического эффекта распределенных и сосредоточенных масс называют скорость, численно равную собственной частоте его изгибных колебаний на подшипниках качения или скольжения при отсутствии вращения. Таким образом, задача определения критических скоростей в данном случае сводится к нахождению собственных частот изгибных колебаний невращающегося вала. При необходимости учета гироскопического эффекта критическая скорость вала определяется с учетом скорости его вращения.

При критической скорости амплитуды вынужденных колебаний, вызванных неуравновешенностью, становятся бесконечно большими (без учета демпфирования и нелинейности системы). Такой случай в инженерной практике называется резонансом.

Если угловая скорость вращения вала равна угловой скорости обратной прецессии, то она называется критической скоростью, соответствующей обратной прецессии. При этом значении угловой скорости неуравновешенность ротора не приводит к резонансным явлениям.

Знание точных значений критических скоростей прямой прецессии (в дальнейшем – критических скоростей) крайне важно, так как позволяет правильно отстроить рабочие скорости от резонансных зон.

Если угловая скорость вала меньше первой критической, то вал условно называют жестким, а если больше первой критической – гибким; для жестких валов рекомендуется соотношение , для гибких – где и - соответственно первая и вторая критические скорости.

1.1 Метод начальных параметров

В отечественной и зарубежной литературе описываются различные методы определения критических скоростей валов [3, 5, 6, 8, 9]. Наибольшее число исследований посвящено валам постоянного сечения. Для валов переменного сечения в инженерной практике широкое применение получил метод начальных параметров, наиболее удобный для расчета сложных упругих систем.

Метод начальных параметров был впервые предложен академиком А.Н.Крыловым для определения критических скоростей однопролетных валов постоянного сечения, несущих несколько дисков /10/. В дальнейшем этот метод получил развитие в работах Е.Б.Лунца, Н.И.Безухова, М.Я.Кущуля, А.А.Щеглова и некоторых других российских и зарубежных авторов.

При проведении численных расчетов методом начальных параметров вал с непрерывно изменяющимся сечением заменяется ступенчатым и разделяется на цилиндрические и конические участки. Нумерация участков проводится слева-направо: 0, 1, 2 и т.д. Границами участков служат места, в которых либо скачком изменяется поперечное сечение, либо расположена опора, либо приложены внешние момент или сила, либо, наконец, вал сопрягается с насаженными на него деталями. Начало координаты выбирается в начале каждого участка вала, а направление оси принимается для всех участков одинаковым – вниз. Используется следующее правило знаков: внешние силы, действующие на вал, считаются положительными, если они направлены вниз (в сторону положительных прогибов), а моменты – по часовой стрелке.

1.1.1 Цилиндрический вал

Дифференциальное уравнение упругой линии -го участка вала, совершающего прямую прецессию, имеет вид [5]

, (1.1)

где	-параметр, являющийся для данного участка вала функцией скорости;
, здесь и		-соответственно масса единицы длины и
	жесткость -го участка вала,
	-искомая критическая скорость вала.

Общий интеграл дифференциального уравнения (1.1) для -го цилиндрического участка вала

, (1.2)

где
и	-постоянные интегрирования;
и	-нормальные фундаментальные решения уравнения (1.1) или функции частот:

причем

		(1.3)

Дифференцируя выражение (1.2) последовательно по , получим

	(1.4)
.

Пусть на границе двух участков и приложены сосредоточенная внешняя сила и момент (рисунок 1,а). Тогда в точке с абсциссой условия сопряжения между участниками будут

	(1.5)

Первые два условия следуют из непрерывности упругой линии и её первой производной, вторые два – из равновесия бесконечно малого элемента, содержащего точку . Изгибающие моменты и поперечные силы в равенствах (1.5) берутся справа и слева от сечения на бесконечно близком расстоянии от него.

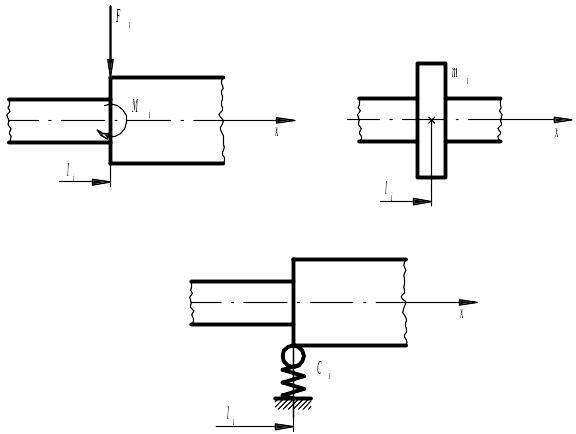
Рисунок 1 – Случаи сопряжения участков вала

Из выражений (1.5) можно получить условия сопряжения для различных частных случаев. Так, если на границе двух смежных участков вала закреплен диск с массой (рисунок 1,б), то условия сопряжения примут вид

где - гироскопический момент диска,

здесь - разность между полярным и осевым моментами инерции диска с массой ; величина может быть как положительной (в случае диска), так и отрицательной (в случае цилиндра, вытянутого вдоль оси вала);

- центробежная сила инерции диска,

Если на границе двух смежных участков вала расположена упругая линейная шарнирная опора с коэффициентом жесткости , то условия сопряжения будут

Приложенные в местах сопряжения внешние силы и моменты в каждом отдельном случае должны быть определены.

В машинах и аппаратах самых разнообразных назначений валы часто несут на себе длинные детали, опирающиеся на вал в двух и более местах, как, например, барабаны, втулки, шнеки и т.п. Во многих случаях при изучении изгибных колебаний можно с достаточной точностью такие детали рассматривать как балку переменного сечения. Таким образом, возникает задача о критических скоростях составных валов. Условия сопряжения составных валов значительно сложнее рассмотренных и подробно исследованы в монографии М.Я.Кущуля [5].

Решение задачи определения критических скоростей начинается с рассмотрения условий закрепления левого конца вала.

Например, в случае жесткой шарнирной опоры (рисунок 2,а) прогиб и изгибающий момент в начале нулевого участка равны нулю, то есть и . Тогда из уравнений (1.2) и (1.4) с учетом выражений (1.3) следует, что .

При жестком защемлении левого конца вала (рисунок 2, б) прогиб и угол поворота в начале нулевого участка равны нулю, то есть и . Отсюда .

В случае свободного левого конца вала (рисунок 2, в) изгибающий момент и поперечная сила в начале нулевого участка равны нулю, то есть и . Отсюда .

В случае упругой шарнирной линейной опоры с коэффициентом жесткости (рисунок 2, г) имеем

Отсюда или

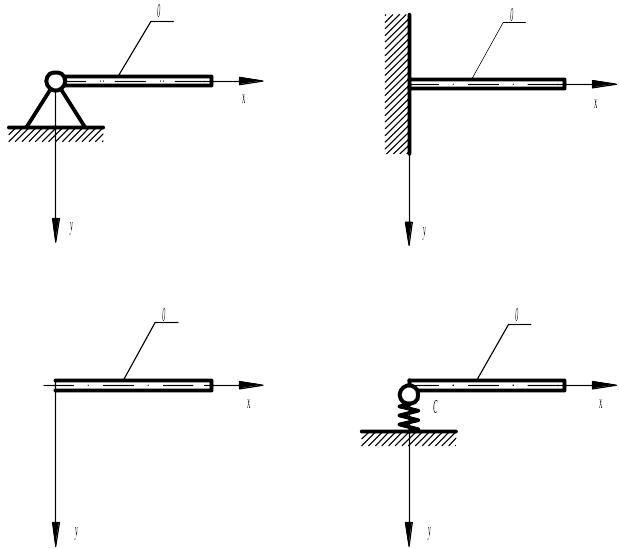
Рисунок 2 – Варианты закрепления левого конца вала

Таким образом, каковы бы ни были условия закрепления левого конца вала, две из четырех постоянных интегрирования могут быть исключены.

Определение критических скоростей проводится в следующей последовательности. Исходя из какой-либо приближенной оценки или из опыта проведения подобных расчетов, задаются численным значением критической скорости того или иного порядка. Вычисляют значения коэффициентов , аргументов и функций частот для всех участков вала. Далее рассматривают условия закрепления левого конца вала.

Основная идея метода начальных параметров состоит в том, чтобы, используя условия сопряжения, выразить постоянные интегрирования последующего -го участка через постоянные интегрирования предыдущего -го участка.

После рассмотрения условий закрепления правого конца вала задача сводится к решению двух линейных, однородных алгебраических уравнений относительно двух начальных параметров. Если заданная угловая скорость – критическая, то система этих уравнений имеет нетривиальное решение, её детерминант ; в противном случае строится кривая зависимости величины детерминанта (так называемого «остатка») от задаваемых значений критических скоростей (рисунок 3). Точки пересечения этой кривой с осью абсцисс дают значения критических скоростей различных порядков. Обычно бывает достаточно двух-трех расчетов, чтобы, интерполируя, определить критическую скорость с нужной для инженерных расчетов точностью.

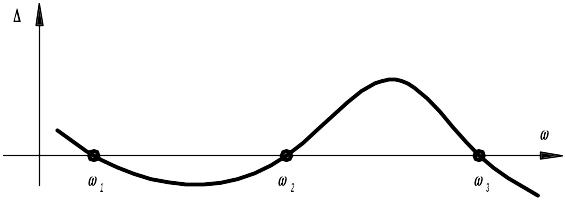
Рисунок 3 – Зависимость детерминанта от угловой скорости вала

В отличие от вариационных методов, где сложность вычислений возрастает вместе с порядком критической скорости, метод начальных параметров дает возможность определять критические скорости всех порядков совершенно одинаково. Однообразие выкладок при этом методе позволяет значительно ускорить расчетную работу путем применения электронно-вычислительных машин.

1.1.2 Конический вал

При расчете многоступенчатых валов с небольшим числом сосредоточенных масс каждая совокупность из нескольких цилиндрических участков, расположенных между массами, может быть заменена одним коническим участком. Вследствие этого число участков, вводимых в расчет, значительно уменьшается. В этом случае, а также в случае наличия конических участков может быть применена так называемая теория конического вала. Подробное изложение этой теории приведено в работе [11].

Упругая линия конического вала, совершающего прямую прецессию с угловой скоростью , описывается уравнением

, (1.6)

где и	-постоянные интегрирования;
и	-частные решения, составляющие нормальную фундаментальную систему;
	-параметр, являющийся для данного вала функцией скорости; , здесь и - соответственно массы единицы длины вала и изгибная жесткость в начальном сечении
	-относительная абсцисса произвольного сечения вала, определяемая формулой , здесь - расстояние от начала координат до точки пересечения образующих конуса (рисунок 4).

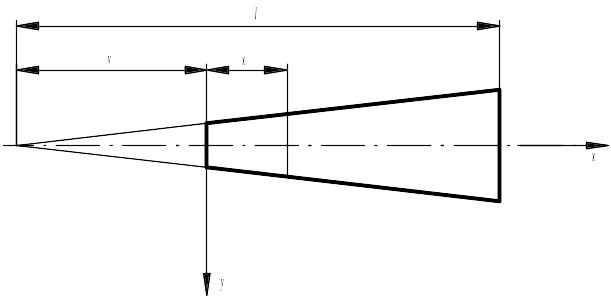
Рисунок 4 – Схема конического вала

В случае вала с уменьшающимся диаметром параметры и являются отрицательными.

В качестве частных решений в уравнении (1.6) выбраны функции, составляющие нормальную фундаментальную систему, то есть подчиненные единичной матрице.

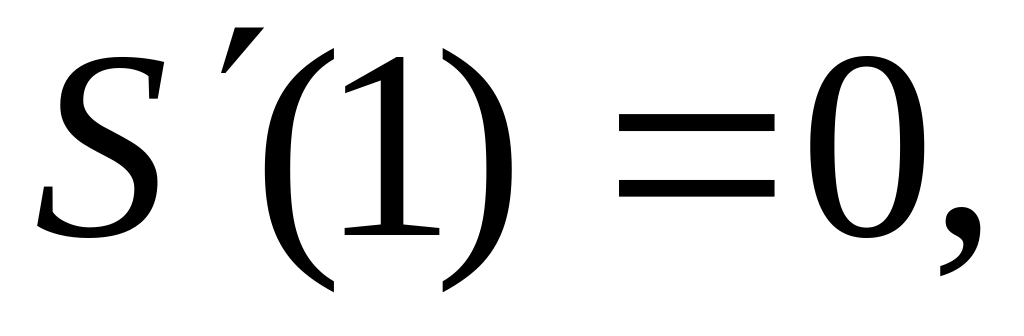
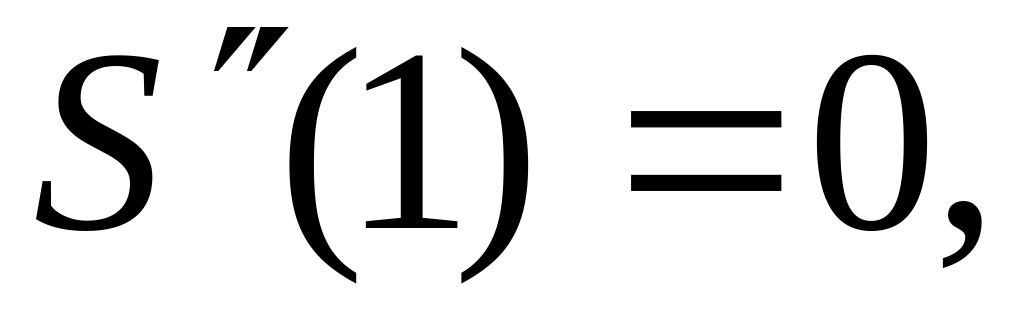
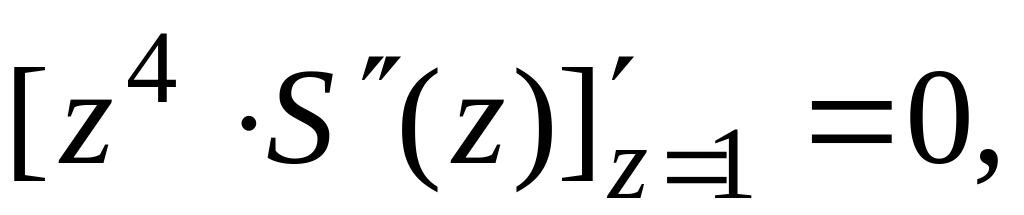
				(1.7)

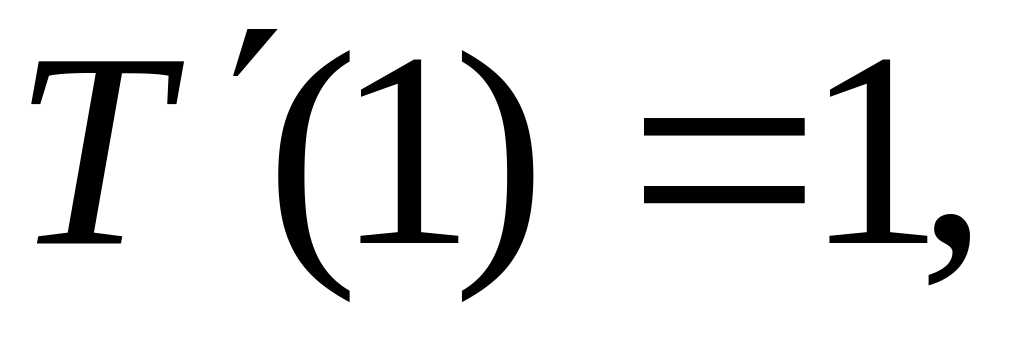
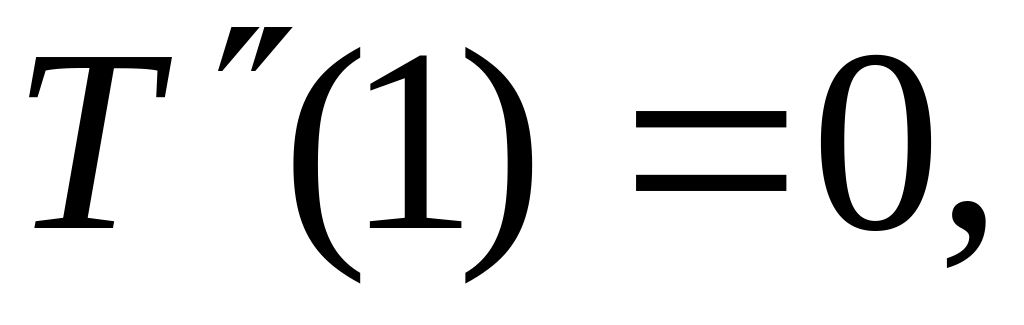
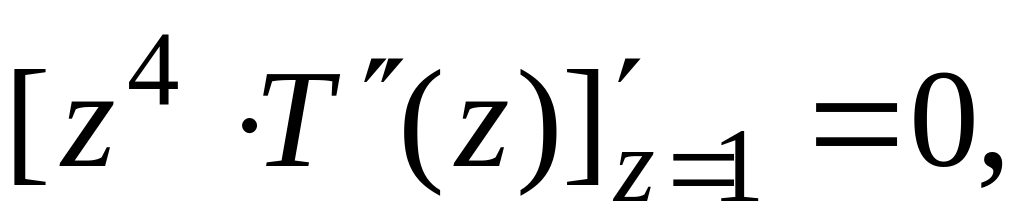
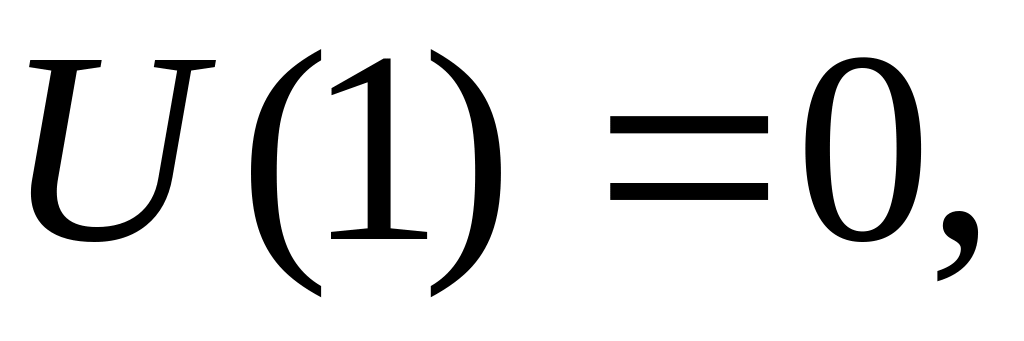
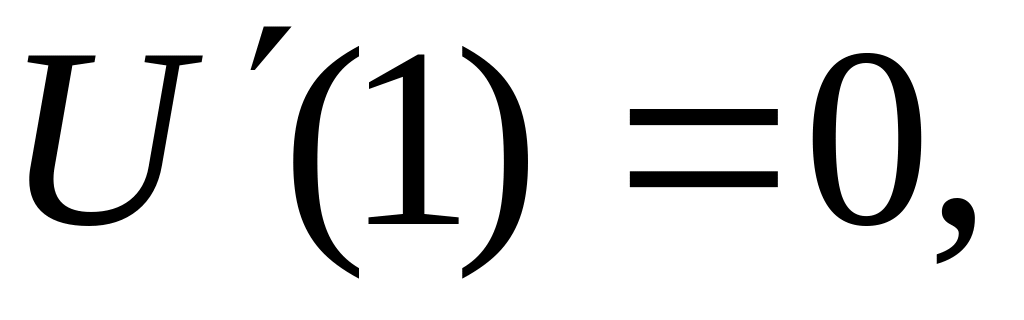
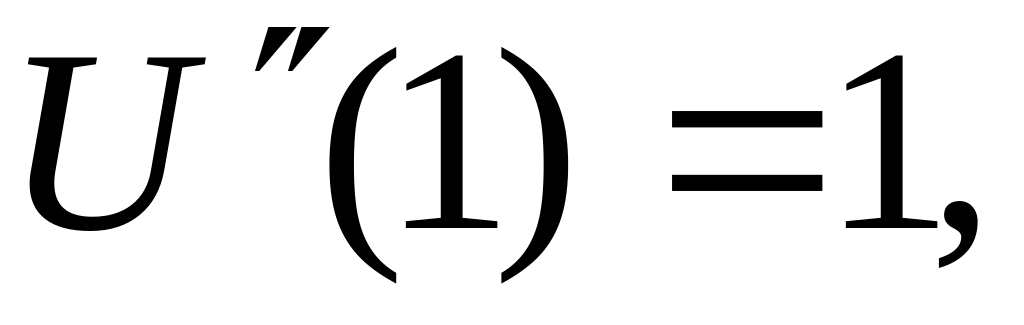
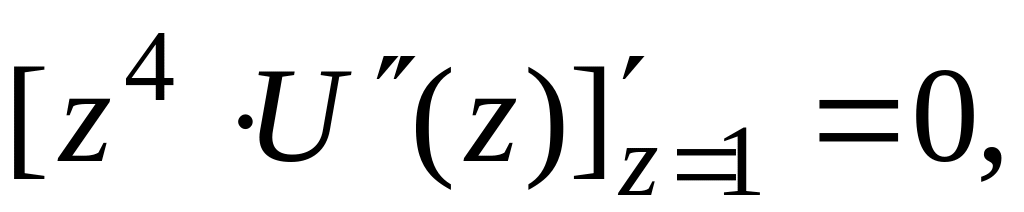
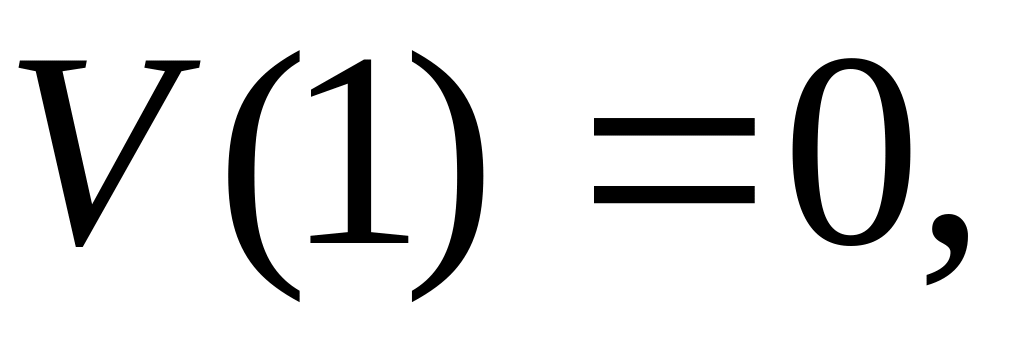
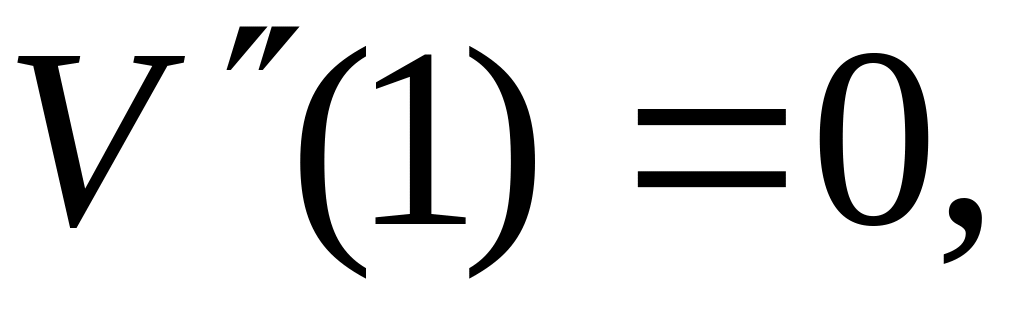
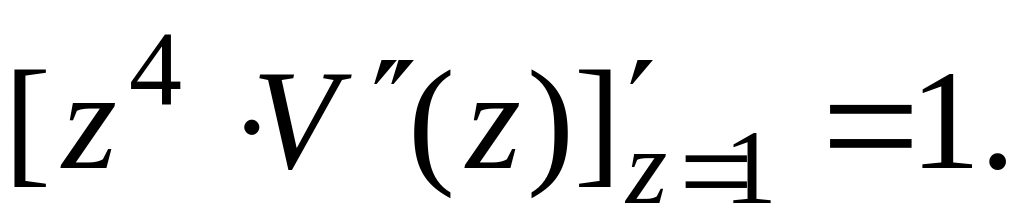
Функции и определяются из выражений

где и

-функции Бесселя второго порядка, вычисляемые для аргумента (аргумент для краткости опущен) и образующие фундаментальную систему решений исходного дифференциального уравнения.

Постоянные коэффициенты определяются из условий матрицы (1.7) и равны

где и

-функции Бесселя соответственно третьего и четвертого порядков, вычисляемые для аргумента .

Табличные значения функций Бесселя приведены в работе [12].

Поскольку общий интеграл (1.6) составлен из функций, образующих нормальную фундаментальную систему решений, то, как известно, постоянные при последних оказываются равными начальным параметрам или величинам, им пропорциональным. В данном случае можно записать

где и

-соответственно прогиб, угол поворота, изгибающий момент и поперечная сила в начале координат.

Для частных случаев опирания левого конца вала имеем:

в случае жесткой шарнирной опоры

в случае заделки

в случае свободного конца

Для всех случаев сопряжения участков вала граничные условия в общем виде записываются одинаково

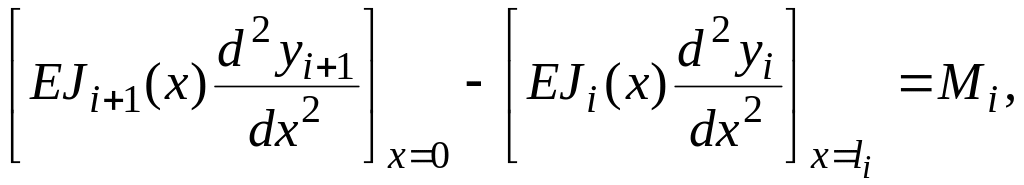
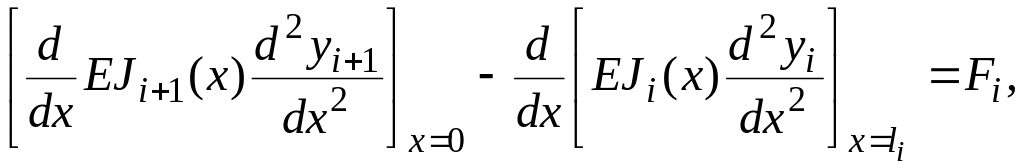
где	-внешний момент и сосредоточенная сила, приложенные в рассматриваемом сечении .

Для составления условий сопряжения необходимо иметь производные функций и . Эти производные приведены в таблице 1.

Таблица 1 – Производные функций частот

Функции, входящие в табл. 1, определяются формулами

,

В приведенных формулах аргумент функций Бесселя, равный , для краткости опущен.

Критические скорости определяются методом остатка в той же последовательности, что и в случае цилиндрического вала.

1.2 Составление расчетной схемы вала

Составление расчетной схемы является одним из ответственнейших этапов при расчете критических скоростей валов.

Валы машин и аппаратов, используемых в химической промышленности, как правило, представляют собой двухопорные валы переменного сечения с несколькими распределенными и сосредоточенными нагрузками. Определение критических скоростей таких валов является достаточно сложной и трудоемкой задачей, причем сложность решения этой задачи существенно зависит от расчетной схемы вала.

В связи с этим при составлении расчетной схемы конструктор часто стоит перед дилеммой: с одной стороны, для более точного решения задачи необходимо учесть максимально-возможное количество факторов, влияющих на критические скорости вала; с другой стороны, ряд факторов желательно было бы отбросить, что существенно могло бы упростить расчетную схему вала. Однако для этого необходимо точно знать, влиянием каких факторов можно пренебречь при данных конструктивных соотношениях параметров как самого вала, так и деталей узлов, вращающихся вместе с валом.

Практика проектирования показывает, что на стадиях эскизной и технической проработки конструкции размеры отдельных деталей и узлов машины претерпевают неоднократные изменения. Это вызывает необходимость многократного проведения трудоемких расчетов для различных конструктивных вариантов. Внедрение ЭВМ в расчетную практику может значительно упростить решение данной задачи.

В качестве примера на рисунке 5 приведен узел вращения одной из промышленных центрифуг.

Вал центрифуги – цилиндрический переменного сечения на двух опорах – верхней и нижней. Верхняя опора образована двумя спаренными радиально-упорными шарикоподшипниками 2, наружные кольца которых закреплены в жестком корпусе. Нижняя опора – радиальный шарикоподшипник 5, наружное кольцо которого вмонтировано в упругую опору 4.

Вместе с валом вращаются следующие детали и узлы: на верхнем конце вала – соединительная полумуфта 1; над нижней опорой – детали узла крепления подшипника 5; между нижней опорой и ротором 7 – детали узла уплотнения 6; на нижнем конце вала – мешалка 9 и рабочее колесо центробежного насоса 10.

На основании теоретических и экспериментальных исследований [13, 14], а также опыта эксплуатации центрифуг данного типа при составлении расчетной схемы вала (рисунок 6) принимается следующее:

1) верхняя опора вала принимается упругой с коэффициентом жесткости так как она расположена в достаточно массивном, жестко закрепленном корпусе. Сдвоенные подшипники качения, расположенные рядом, считаются шарнирной опорой; в качестве межопорного расстояния принимается расстояние от центра нижнего подшипника до середины верхней опоры;

2) характеристика нижней упругой опоры принимается линейной и изотропной; коэффициент жесткости опоры ;

3) масса соединительной полумуфты учитывается в виде сосредоточенной массы , приложенной в центре тяжести полумуфты. Эта масса в расчетах не учитывается, если отношение , а отношение . Гироскопический момент полумуфты не учитывается;

4) масса деталей узла крепления нижнего подшипника учитывается в виде приведенной сосредоточенной массы , закрепленной в месте ступенчатого изменения диаметра вала;

5) масса деталей узла уплотнения учитывается в виде приведенной сосредоточенной массы , закрепленной в месте расположения упругой опоры;

6) ротор центрифуги считается абсолютно жестким. Точкой закрепления массы ротора принимается середина посадочной ступицы. Расстояние от центра тяжести ротора до середины посадочной ступицы обозначается отрезком . Небольшие детали вблизи ротора не учитываются,

если отношение их массы к массе ротора не превышает 0,005. В противном случае их масса приводится к массе ротора;

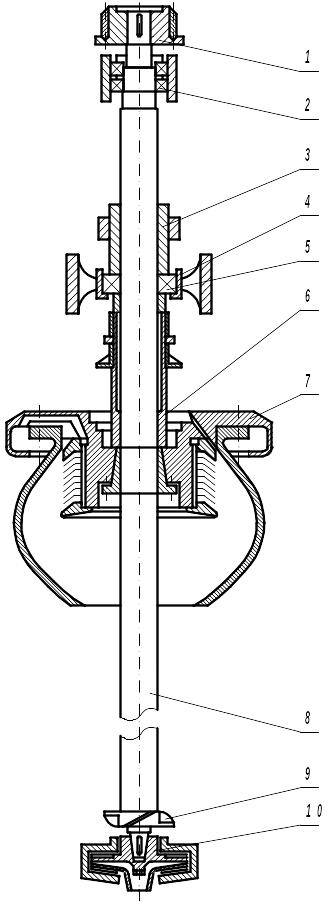
1 – соединительная полумуфта; 2 – радиально‑упорные подшипники качения; 3 – узел крепления радиального подшипника; 4 – упругая опора; 5 – радиальный подшипник; 6 – узел уплотнений; 7 - ротор; 8 – вал; 9 – мешалка; 10 – центробежный насос.

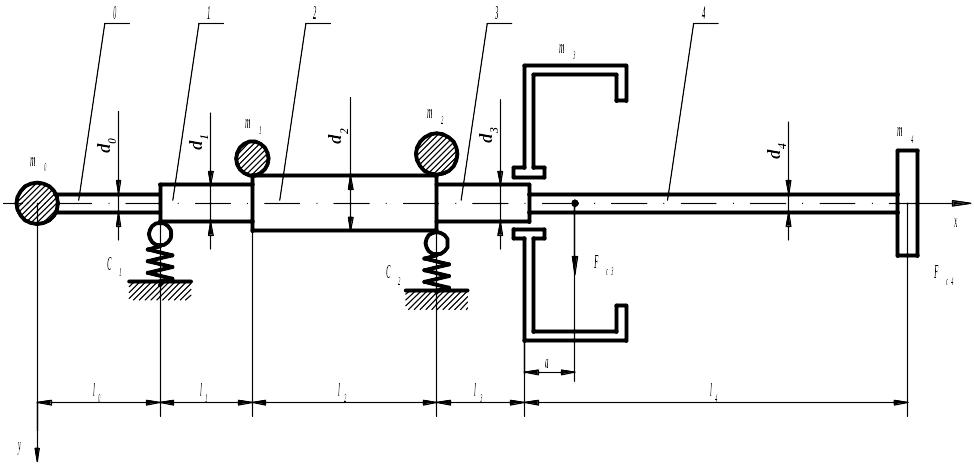
Рисунок 6 – Расчетная схема вала центрифуги

7) рабочее колесо центробежного насоса представляется в виде диска, центр тяжести которого совпадает с центром тяжести рабочего колеса, а масса равна его массе;

8) два участка вала, отношение диаметров которых не превышает величины 1,05, а отношение длин – величины 1,1, могут быть приняты за один участок.

Данные рекомендации по составлению расчетной схемы вала получены для определенного типа центрифуг и, естественно, не могут носить универсального характера. Подобные рекомендации должны разрабатываться для каждого класса и типоразмера машин на основании специальных исследований и опыта эксплуатации.

1.3 Вывод расчетных зависимостей

В качестве примера рассмотрим вывод расчетных зависимостей для вала, схема которого представлена на рисунке 6. Вал разбивается на участки: нулевой, первый, второй, третий и четвертый. При выводе расчетных зависимостей дополнительно к ранее принятым вводятся следующие условные обозначения:

	- диаметры соответствующих участков вала;
	- осевые моменты инерции сечений соответствующих участков вала;
	-длины соответствующих участков вала;
	- разность между полярным и осевым моментами инерции соответственно масс и ;
	- гироскопические моменты масс и ;
	- центробежные силы инерции масс и ;
	- коэффициенты жесткости соответственно верхней и нижней упругих опор;
	- расстояние от центра тяжести до точки закрепления массы ротора.

Нулевой участок

Уравнения упругой линии нулевого участка вала и первых трех производных имеют вид

(1.8)

где - здесь - искомая критическая скорость вала.

Краевые условия на левом конце вала

Тогда или (1.9)

или (1.10)

где

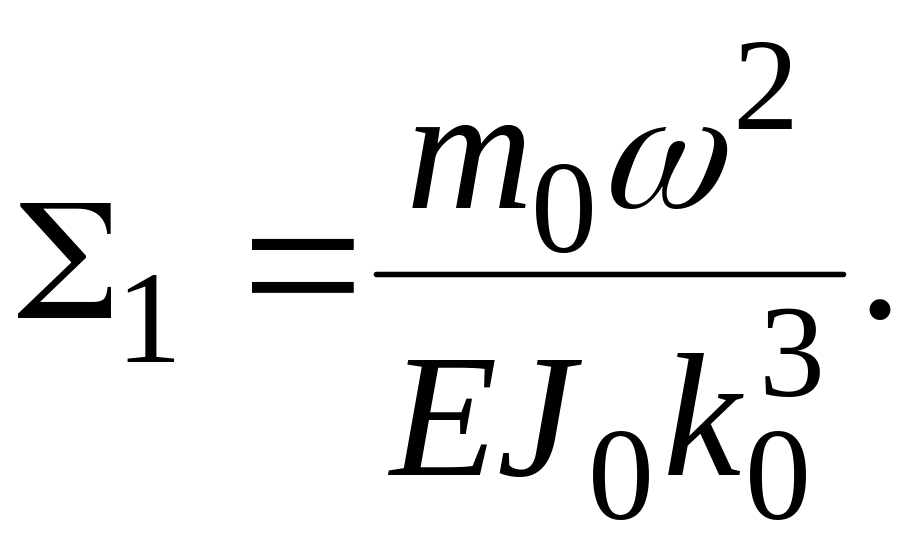
При с учетом (1.9) и (1.10) выражения (1.8) запишутся

(1.11)

где

Первый участок

Уравнения упругой линии первого участка вала и первых трех производных

(1.12)

где .

При уравнения (1.12) примут вид

(1.13)

Условия сопряжения нулевого и первого участков вала

(1.14)

Путем подстановки (1.11) и (1.13) в условия сопряжения (1.14) определяются произвольные постоянные и

(1.15)

где

С учетом (1.15) при уравнения (1.12) запишутся

,

(1.16)

где

здесь

Второй участок

Уравнения упругой линии второго участка вала и первых трех производных

(1.17)

где .

При уравнения (1.17) примут вид

(1.18)

Условия сопряжения первого и второго участков вала

(1.19)

.

Путем подстановки (1.16) и (1.18) в условия сопряжения (1.19) определяются постоянные интегрирования и

(1.20)

где

С учетом (1.20) при уравнения (1.17) запишутся

(1.21)

где

здесь .

Третий участок

Уравнения упругой линии третьего участка вала и первых трех производных

,

,

(1.22)

,

,

где .

При уравнения (1.22) примут вид

. (1.23)

Условия сопряжения второго и третьего участков вала

,

,

(1.24)

,

.

Путем подстановки (1.21) и (1.23) в условия сопряжения (1.24) определяются постоянные интегрирования и

,

,

(1.25)

где

С учетом (1.25) при уравнения (1.22) запишутся

,

,

(1.26)

,

где ,

,

,

,

,

,

,

,

здесь .

Четвертый участок

Уравнение упругой линии четвертого участка вала и первых трех производных

(1.27)

где .

При уравнения (1.27) примут вид

(1.28)

Условия сопряжения третьего и четвертого участков вала

(1.29)

где

Путем подстановки (1.26) и (1.28) в условия сопряжения (1.29) определяются постоянные интегрирования и

(1.30)

где

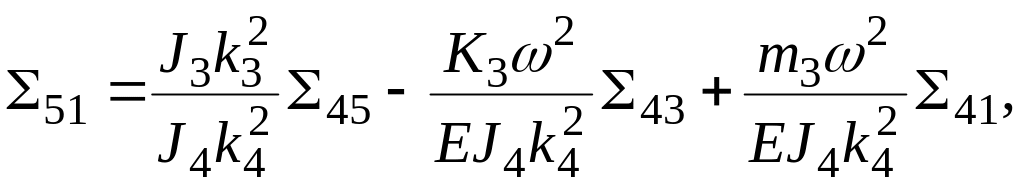
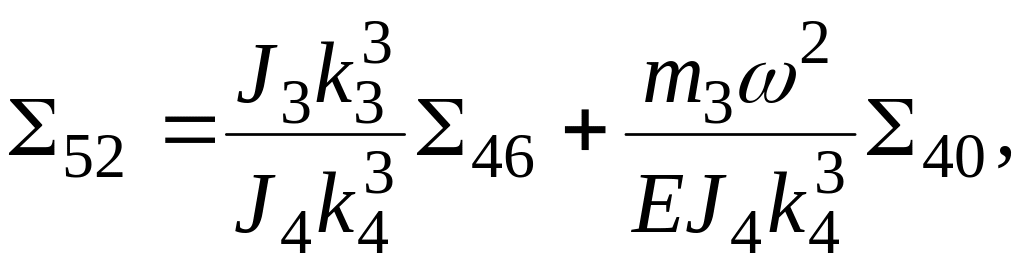
С учетом (1.30) при уравнения (1.27) запишутся

(1.31)

где

здесь .

Краевые условия на правом конце вала

(1.32)

где (1.33)

С учетом выражений (1.31) и (1.33) после алгебраических преобразований краевые условия (1.32) окончательно запишутся в виде

(1.34)

где

Таким образом, задача сводится к решению системы из двух линейных однородных алгебраических уравнений (1.34) относительно начальных параметров и . Детерминант этой системы

Если заданная угловая скорость -критическая, то детерминант должен быть равен нулю. В противном случае следует задаться новым значением угловой скорости и расчет повторить.

На рисунке 7 приведены расчетные схемы валов, которые получили достаточно широкое распространение в химическом машиностроении, особенно в центрифугостроении. Сравнительная простота этих схем позволяет вывести трансцендентные уравнения для определения критических скоростей валов любого порядка. Вывод трансцендентных уравнений производится методом начальных параметров, как и для расчетной схемы вала, представленной на рисунке 6, поэтому приведем их в окончательном виде [15]:

д л я с х е м ы (см. рисунок 7, а)

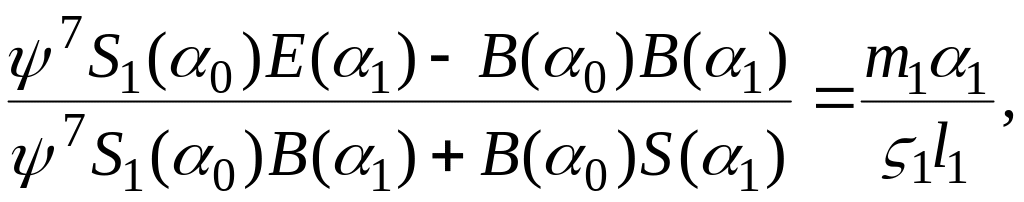
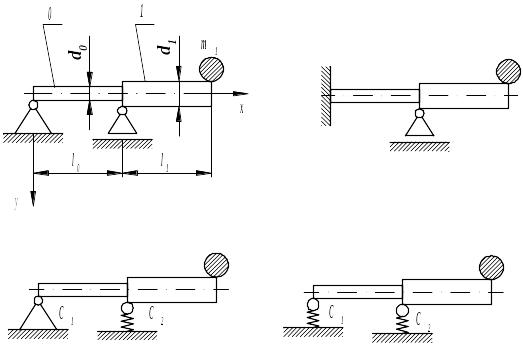
Рисунок 7 – Расчетные схемы валов

д л я с х е м ы (см. рисунок 7, б)

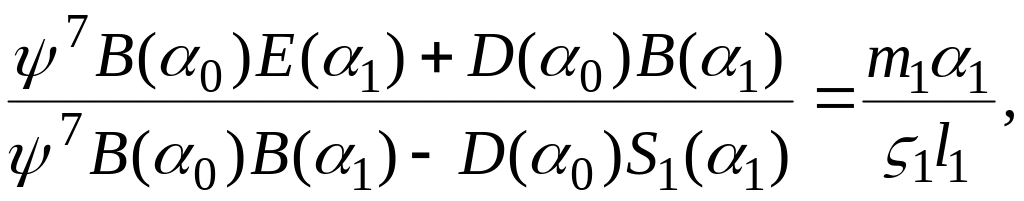
д л я с х е м ы (см. рисунок 7, в)

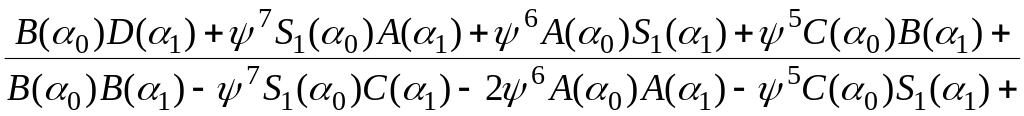
д л я с х е м ы (см. рисунок 7, г)

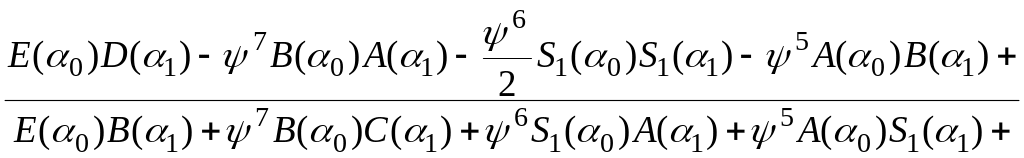
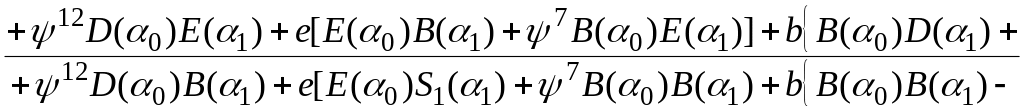
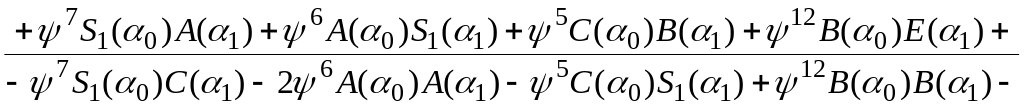
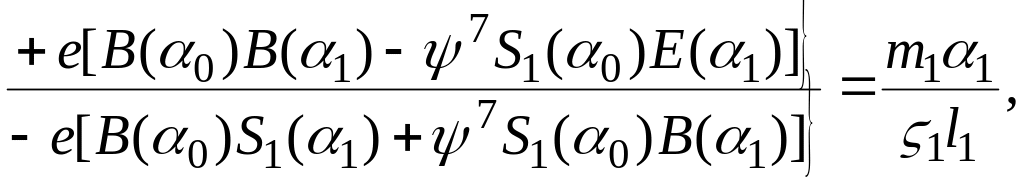
где 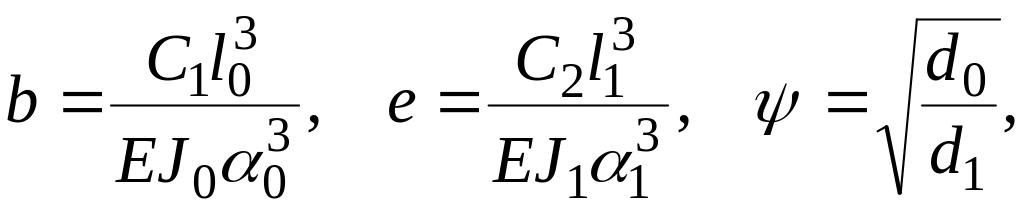здесь и - аргументы функций частот, определяемые по формулам: и - функции частот [16]

Определение критических скоростей по приведенным трансцендентным уравнениям производится методом подбора в следующем порядке:

1) задаются значением угловой скорости ;

2) по формуле определяются коэффициенты и ;

3) определяются аргументы и функций частот;

4) по таблицам [15] находятся значения функций частот и подставляются в полученные уравнения;

5) в случае равенства левой и правой частей уравнения заданная угловая скорость будет равна критической, а в случае неравенства – задаются новым значением и весь порядок расчета повторяется заново.

Использование подобных уравнений в инженерной практике позволяет значительно сократить время на проведение расчетных работ по определению критических скоростей валов.