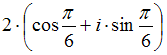Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[-
;
],
не
является
…
на
[-
;
],
не
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямоугольные координаты на плоскости Точки и лежат на одной прямой, параллельной оси ординат. Расстояние между точками и равно 6. Тогда положительные координаты точки равны …
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
|
Тема:
Прямоугольные координаты на плоскости
Даны
точки
![]() и
и
![]() .
Тогда координаты точки
.
Тогда координаты точки
![]() ,
симметричной точке
относительно
точки
,
равны …
,
симметричной точке
относительно
точки
,
равны …
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямая на плоскости Уравнение прямой, проходящей через точку пересечения прямых и перпендикулярно прямой имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Прямая на плоскости
Прямые
![]() и
и
![]() …
…
|
|
|
перпендикулярны |
|
|
|
пересекаются под острым углом |
|
|
|
совпадают |
|
|
|
параллельны |
Тема: Прямая на плоскости
Прямая
отсекает на оси
отрезок
![]() и
имеет угловой коэффициент
и
имеет угловой коэффициент
![]() .
Тогда ее уравнение имеет вид …
.
Тогда ее уравнение имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
6 |
|
|
|
7 |
|
|
|
|
|
|
|
|
Тема: Градиент скалярного поля Градиент скалярного поля в точке пересечения оси с поверхностью равен …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Градиент скалярного поля
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
3 |
|
|
|
9 |
|
|
|
|
|
|
|
|
Тема:
Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
Тема:
Дифференциальное исчисление
ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() ,
вычисленное с помощью полного
дифференциала, равно …
,
вычисленное с помощью полного
дифференциала, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Непрерывность функции, точки разрыва
Функция
 непрерывна
на отрезке …
непрерывна
на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле Коэффициент в разложении в ряд Фурье функции на интервале равен …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Гармонические колебания
Амплитуда
гармонических колебаний равна
![]() ;
угловая частота равна
рад.;
а начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
;
угловая частота равна
рад.;
а начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
![]() составляет …
составляет …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямоугольные координаты на плоскости Даны точки и . Тогда координаты точки , симметричной точке относительно точки , равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Поверхности второго порядка
Даны
уравнения поверхностей второго
порядка:
А)
 B)
B)
 C)
C)
 D)
D)
 Тогда
двуполостный гиперболоид задается
уравнением …
Тогда
двуполостный гиперболоид задается
уравнением …
|
|
|
B |
|
|
|
C |
|
|
|
A |
|
|
|
D |
Тема: Полная вероятность. Формулы Байеса Банк выдает 44% всех кредитов юридическим лицам, а 56% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,2; а для физического лица эта вероятность составляет 0,1. Тогда вероятность того, что очередной кредит будет погашен в срок, равна …
|
|
|
0,856 |
|
|
|
0,144 |
|
|
|
0,85 |
|
|
|
0,866 |
Тема: Определение вероятности Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Числовые характеристики случайных величин Дисперсия дискретной случайной величины , заданной законом распределения вероятностей: равна 0,06. Тогда значение равно …
|
|
|
1,5 |
|
|
|
0,5 |
|
|
|
3 |
|
|
|
6 |
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
ее функция распределения вероятностей
имеет вид …
Тогда
ее функция распределения вероятностей
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Численное дифференцирование и
интегрирование
Значение
дифференцируемой функции
в
точке
![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Сходимость числовых рядов
Сумма
числового ряда
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
1 |
Тема: Базис и размерность линейного пространства За базис трехмерного векторного пространства можно принять совокупность векторов …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Базис и размерность линейного пространства Разложение вектора по векторам и имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Норма вектора в евклидовом пространстве Даны векторы и , угол между которыми равен . Проекция вектора на вектор равна . Тогда норма вектора равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
При решении системы дифференциальных уравнений
 можно
получить уравнение второго порядка
вида …
можно
получить уравнение второго порядка
вида …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Метрические пространства
Функция
![]() ,
где
,
где ![]() и
и
![]() ,
…
,
…
|
|
|
не удовлетворяет аксиоме треугольника |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
Тема:
Мера плоского множества
Мера
плоского множества
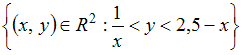 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Тема:
Точечные оценки параметров распределения
Из
генеральной совокупности извлечена
выборка объема
:
 Тогда
выборочная дисперсия равна …
Тогда
выборочная дисперсия равна …
|
|
|
0,84 |
|
|
|
11,4 |
|
|
|
0,94 |
|
|
|
1,0 |
Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Элементы корреляционного анализа
При
построении выборочного уравнения парной
регрессии вычислены выборочный
коэффициент корреляции
![]() и
выборочные средние квадратические
отклонения
и
выборочные средние квадратические
отклонения
![]() .
Тогда выборочный коэффициент регрессии
Y
на X
равен …
.
Тогда выборочный коэффициент регрессии
Y
на X
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Умножение матриц Матрица , где и . Тогда элемент равен …
|
|
|
11 |
|
|
|
– 10 |
|
|
|
– 11 |
|
|
|
10 |
Тема: Вычисление определителей Определитель равен …
|
|
|
45 |
|
|
|
135 |
|
|
|
– 45 |
|
|
|
– 135 |
Тема: Численное дифференцирование и интегрирование Значение дифференцируемой функции в точке можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Численные методы решения дифференциальных
уравнений и систем
Решение
дифференциального уравнения
![]() на
отрезке
на
отрезке
![]() с
шагом
с
шагом
![]() ,
при начальном условии
,
в точке
по
методу Эйлера может быть найдено как …
,
при начальном условии
,
в точке
по
методу Эйлера может быть найдено как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Числовые последовательности Из числовых последовательностей , , , не является сходящейся последовательность …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Сходимость числовых рядов Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
|
|
|
ряд А) расходится, ряд В) расходится |
|
|
|
ряд А) сходится, ряд В) сходится |
|
|
|
ряд А) расходится, ряд В) сходится |
Тема:
Отображение множеств
Образом
отрезка
 при
отображении
при
отображении
![]() является
отрезок …
является
отрезок …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Метрические пространства
Функция
 заданная
на множестве целых чисел …
заданная
на множестве целых чисел …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
Тема:
Элементы теории множеств
Даны
множества:
![]() и
и
![]() .
Тогда число элементов, принадлежащих
их пересечению равно …
.
Тогда число элементов, принадлежащих
их пересечению равно …
|
3
|
|
Тема: Типы дифференциальных уравнений Уравнение является …
|
|
|
дифференциальным уравнением первого порядка в полных дифференциалах |
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
Тема: Векторное произведение векторов Векторное произведение векторов и равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Если
и
являются
решением системы линейных уравнений
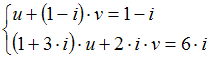 ,
то
,
то
![]() равно
…
равно
…
|
|
|
2 |
|
|
|
|
|
|
|
32 |
|
|
|
0 |
Тема:
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференциальное исчисление ФНП
Частная
производная
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Непрерывность функции, точки разрыва
Функция
 не
является непрерывной на отрезке …
не
является непрерывной на отрезке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Точечные оценки параметров распределения В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …
|
|
|
0,13 |
|
|
|
0,065 |
|
|
|
3,9 |
|
|
|
0,7 |
Тема:
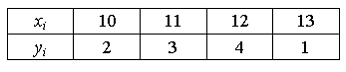
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
представлена
таблицей:
 Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
|
|
|
5,5 |
|
|
|
11 |
|
|
|
6 |
|
|
|
0 |
Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочное среднее признака равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Точечные оценки параметров распределения В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
|
|
|
11,25 |
|
|
|
19,5 |
|
|
|
15 |
|
|
|
21,25 |
|
|
|
|
Тема:
Интервальные оценки параметров
распределения
Дан
доверительный интервал
![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точность этой оценки
равна …
|
|
|
1,12 |
|
|
|
0,01 |
|
|
|
2,24 |
|
|
|
13,56 |
Тема:
Градиент скалярного поля
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
4 |
Тема: Норма вектора в евклидовом пространстве Если и – ортогональные векторы из евклидова пространства со стандартным скалярным произведением, такие что , , то норма вектора равна …
|
|
10 |
|
|
25 |
|
|
5 |
|
|
7 |
Тема:
Норма вектора в евклидовом пространстве
Даны
векторы
и
![]() ,
угол между которыми равен
.
Тогда проекция вектора
на
вектор
равна …
,
угол между которыми равен
.
Тогда проекция вектора
на
вектор
равна …
|
|
|
|
|
|
|
– 1 |
|
|
|
3 |
|
|
|
|
Тема:
Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
1 | |
Тема:
Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
![]() на
интервале
равен
…
на
интервале
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции Период функции равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Комплексные числа и их представление
Показательная
форма записи комплексного числа
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Однородные дифференциальные уравнения
Общий
интеграл дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Типы дифференциальных уравнений
Уравнение
![]() является
…
является
…
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
Тема:
Системы линейных уравнений
Решение
системы линейных уравнений
 методом
Крамера может иметь вид …
методом
Крамера может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Умножение матриц
Матрица
,
где
 и
и
 .
Тогда элемент
.
Тогда элемент
![]() равен …
равен …
|
|
|
10 |
|
|
|
4 |
|
|
|
– 3 |
|
|
|
0 |
Тема: Дифференциальное исчисление ФНП Приближенное значение функции в точке , вычисленное с помощью полного дифференциала, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Типы дифференциальных уравнений Уравнение является …
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
линейным дифференциальным уравнением первого порядка |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
|
|
|
уравнением Бернулли |
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Комплексные числа и их представление
Главное
значение аргумента комплексного числа
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференциальное исчисление
ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() ,
вычисленное с помощью полного
дифференциала, равно …
,
вычисленное с помощью полного
дифференциала, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Базис и размерность линейного
пространства
Даны
вектор
![]() и
матрица
и
матрица
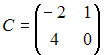 перехода
от старого базиса к новому. Тогда
координаты вектора
в
новом базисе имеют вид …
перехода
от старого базиса к новому. Тогда
координаты вектора
в
новом базисе имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Поверхности второго порядка
Координаты
центра поверхности
![]() равны …
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Типы дифференциальных уравнений
Уравнение
![]() является
…
является
…
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными коэффициентами
Решение
задачи Коши

![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
Тема:
Системы двух линейных дифференциальных
уравнений с постоянными
коэффициентами
Решение
задачи Коши
|
Тема: Полная вероятность. Формулы Байеса Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
|
|
|
|
|
|
|
|
|
|
|
0,07 |
|
|
|
0,05 |
Тема:
Законы распределения вероятностей
дискретных случайных величин
Для
дискретной случайной величины
:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
 Тогда
значение параметра
может
быть равно …
Тогда
значение параметра
может
быть равно …
|
|
|
0,655 |
|
|
|
1 |
|
|
|
0,25 |
|
|
|
0,45 |
Тема:
Метрические пространства
Расстояние
между матрицами
 и
и
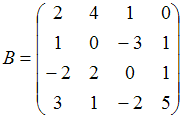 в
метрике
в
метрике
 равно …
равно …
|
|
|
43 |
|
|
|
13 |
|
|
|
2 |
|
|
|
34 |
Тема: Гармонические колебания Гармонические колебания с частотой 0,5 амплитудой колебания и начальной фазой, равной нулю, описывается уравнением …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Гармонические колебания
Угловая
частота гармонических колебаний равна
![]() ,
начальная фаза
рад,
а смещение колеблющейся точки от нулевого
положения через 2 секунды равно 0,1. Тогда
амплитуда гармонических колебаний
составляет …
,
начальная фаза
рад,
а смещение колеблющейся точки от нулевого
положения через 2 секунды равно 0,1. Тогда
амплитуда гармонических колебаний
составляет …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа Функцией, ортогональной к функции на [0, ], не является …
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Элементы гармонического анализа
Разложение
функции
![]() на
гармоники имеет вид …
на
гармоники имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Периодические функции
Период
функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Норма вектора в евклидовом пространстве
Норма
вектора
![]() в
евклидовом пространстве со стандартным
скалярным произведением равна …
в
евклидовом пространстве со стандартным
скалярным произведением равна …
|
|
|
6 |
|
|
|
– 2 |
|
|
|
36 |
|
|
|
10 |
Тема:
Область сходимости степенного ряда
Область
сходимости степенного ряда
 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Числовые последовательности
Предел
числовой последовательности
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Вычисление определителей
Разложение
определителя
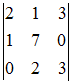 по
строке может иметь вид …
по
строке может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Гармонические колебания
Модуль
скорости точки, совершающей гармонические
колебания, с амплитудой
,
угловой частотой
![]() и
начальной фазой
,
в момент времени
равен …
и
начальной фазой
,
в момент времени
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Тема: Определение вероятности В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() ,
гистограмма относительных частот
которой имеет вид
,
гистограмма относительных частот
которой имеет вид
 Тогда
значение a
равно …
Тогда
значение a
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Векторное произведение векторов
Площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
6 |
Тема:
Линейные дифференциальные уравнения
второго порядка с постоянными
коэффициентами
Общее
решение линейного однородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Типы дифференциальных уравнений Уравнение является …
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
линейным дифференциальным уравнением первого порядка |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
|
|
|
уравнением Бернулли |
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Элементы теории множеств
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
.
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
|
4 |
Тема:
Поверхности второго порядка
Сфера
с центром
![]() проходит
через точку
проходит
через точку
![]() .
Тогда ее уравнение имеет вид …
.
Тогда ее уравнение имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Определитель
системы
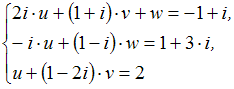 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Линейные дифференциальные уравнения
второго порядка с постоянными
коэффициентами
Общий
вид частного решения
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Область сходимости степенного ряда
Радиус
сходимости степенного ряда
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Числовые последовательности
Числовая
последовательность задана формулой
общего члена
![]() .
Тогда значение
.
Тогда значение
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференциальное исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Периодические функции
Период
функции
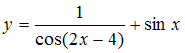 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Поверхности второго порядка
Уравнение
сферы имеет вид
![]() .
Тогда радиус сферы равен …
.
Тогда радиус сферы равен …
|
|
|
7 |
|
|
|
19 |
|
|
|
10 |
|
|
|
49 |
Тема:
Числовые характеристики случайных
величин
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее среднее квадратическое отклонение
равно …
Тогда
ее среднее квадратическое отклонение
равно …
|
|
|
0,80 |
|
|
|
0,64 |
|
|
|
2,60 |
|
|
|
14,16 |
Тема: Полная вероятность. Формулы Байеса В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Определение вероятности Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа Функция представлена таблицей Тогда значение , вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
|
|
|
– 3 |
|
|
|
14 |
|
|
|
|
|
|
|
– 8 |
Тема:
Метрические пространства
Расстояние
между точками
![]() и
и
![]() в
метрике
в
метрике
![]() ,
где
и
,
равно …
,
где
и
,
равно …
|
|
|
10 |
|
|
|
1 |
|
|
|
|
|
|
|
– 1 |
Тема:
Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно …
равно …
|
1 | |
Тема:
Непрерывность функции, точки разрыва
Точка
разрыва функции
 равна
…
равна
…
|
|
|
2 |
|
|
|
– 1 |
|
|
|
3 |
|
|
|
0 |
Тема:
Системы линейных уравнений
Система
 будет …
будет …
|
|
|
совместной и неопределенной |
|
|
|
несовместной и неопределенной |
|
|
|
совместной и определенной |
|
|
|
несовместной и определенной |
Тема:
Ряд Фурье. Теорема Дирихле
Значение
ряда Фурье функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
0 |
|
|
|
– 1 |
|
|
|
1 |
|
|
|
|
Тема: Плоскость в пространстве Плоскость, проходящая через точки и параллельно оси , задается уравнением …
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Однородные дифференциальные
уравнения
Дифференциальное
уравнение
![]() будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
|
|
|
4 |
|
|
|
2 |
|
|
|
0 |
|
|
|
6 |
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: Тогда относительная частота варианты в выборке равна …
|
|
|
0,05 |
|
|
|
0,06 |
|
|
|
0,25 |
|
|
|
0,20 |
Тема:
Числовые характеристики случайных
величин
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
4,6 |
|
|
|
5,0 |
|
|
|
3,0 |
|
|
|
4,9 |
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
число вариант
Тогда
число вариант
![]() в
выборке равно …
в
выборке равно …
|
|
|
32 |
|
|
|
82 |
|
|
|
8 |
|
|
|
31 |
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид
![]() .
Тогда выборочное среднее признака
равно
…
.
Тогда выборочное среднее признака
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Дифференцирование функции комплексного
переменного
Если
и
![]() ,
то мнимая часть производной этой функции
имеет
вид …
,
то мнимая часть производной этой функции
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Системы линейных уравнений с комплексными
коэффициентами
Система
 решается
методом Крамера по формулам
,
,
.
Тогда вспомогательный определитель
решается
методом Крамера по формулам
,
,
.
Тогда вспомогательный определитель
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Определение вероятности В круг радиуса 8 помещен меньший круг радиуса 5. Тогда вероятность того, что точка, наудачу брошенная в больший круг, попадет также и в меньший круг, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Законы распределения вероятностей
дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
ее функция распределения вероятностей
имеет вид …
Тогда
ее функция распределения вероятностей
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Периодические функции
Наименьший
положительный период функции
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямоугольные координаты на плоскости Расстояние между точками и равно 2 при , равном …
|
|
|
1 |
|
|
|
3 |
|
|
|
– 1 |
|
|
|
– 5 |
Тема:
Сходимость числовых рядов
Даны
числовые ряды:
А)
 .
В)
.
В)
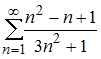 ,
Тогда
…
,
Тогда
…
|
|
|
ряд А) сходится, ряд В) расходится |
|
|
|
ряд А) расходится, ряд В) расходится |
|
|
|
ряд А) сходится, ряд В) сходится |
|
|
|
ряд А) расходится, ряд В) сходится |
Тема: Норма вектора в евклидовом пространстве Скалярное произведение векторов и равно 8, угол между векторами равен , норма вектора равна 4. Тогда норма вектора равна …
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
3 |
Тема:
Градиент скалярного поля
Модуль
градиента скалярного поля
![]() в
точке пересечения оси
с
поверхностью
в
точке пересечения оси
с
поверхностью
![]() равен
…
равен
…
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
Тема:
Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
![]() на
интервале
равен …
на
интервале
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Гармонические колебания
Если
амплитуда гармонических колебаний
равна
![]() и
за 2 минуты совершается 240 колебаний, а
начальная фаза колебаний равна
рад,
то уравнение гармонических колебаний
имеет вид …
и
за 2 минуты совершается 240 колебаний, а
начальная фаза колебаний равна
рад,
то уравнение гармонических колебаний
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Интервальные оценки параметров распределения Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Численные методы решения дифференциальных
уравнений и систем
На
отрезке
задано
дифференциальное уравнение
![]() .
Значение производной второго порядка
в точке
.
Значение производной второго порядка
в точке
![]() может
быть заменено выражением …
может
быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Интерполирование функций: интерполяционные
полиномы Лагранжа
Функция
представлена
таблицей
 Тогда
значение
Тогда
значение
![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
– 6 |
Тема:
Мера плоского множества
Мера
плоского множества
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Тема:
Базис и размерность линейного
пространства
Дано
двухмерное векторное пространства с
базисом
![]() .
Если вектор
.
Если вектор
![]() ,
то вектор
,
то вектор
![]() может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференциальное исчисление ФНП Частная производная второго порядка функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Область сходимости степенного ряда
Радиус
сходимости степенного ряда
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Типы дифференциальных уравнений Уравнение является …
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
|
|
|
дифференциальным уравнением с разделяющимися переменными |
Тема:
Непрерывность функции, точки разрыва
Точка
![]() является
точкой разрыва функции …
является
точкой разрыва функции …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид
![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Численные методы решения дифференциальных
уравнений и систем
Методом
Эйлера решается задача Коши
![]() ,
с
шагом
.
Тогда значение искомой функции
в
точке
будет
равно …
,
с
шагом
.
Тогда значение искомой функции
в
точке
будет
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Плоскость в пространстве
Уравнение
плоскости, проходящей через точку
![]() параллельно
векторам
параллельно
векторам
![]() и
и
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Поверхности второго порядка
Вершина
параболоида
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы теории множеств Даны два множества: и . Тогда количество целых значений , принадлежащих объединению множеств и , равно …
|
8 | |
Тема:
Числовые последовательности
Числовая
последовательность задана формулой
общего члена
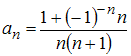 .
Тогда значение
.
Тогда значение
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Числовые характеристики случайных величин Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
Тема:
Численные методы решения дифференциальных
уравнений и систем
Для
задачи Коши
выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
:
 Тогда
значение
Тогда
значение ![]() ,
записанное с двумя знаками после запятой,
равно …
,
записанное с двумя знаками после запятой,
равно …
|
|
|
1,12 |
|
|
|
0,9155 |
|
|
|
1,11 |
|
|
|
1,1155 |
Тема:
Градиент скалярного поля
Градиент
скалярного поля
![]() равен
нулевому вектору в точке …
равен
нулевому вектору в точке …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Векторное произведение векторов
Даны
два вектора:
![]() и
и
![]() .
Тогда вектор
.
Тогда вектор
![]() будет
перпендикулярен и вектору
,
и вектору
,
при
равном
…
будет
перпендикулярен и вектору
,
и вектору
,
при
равном
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Интервальные оценки параметров распределения Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема
,
полигон относительных частот которой
имеет вид:
 Тогда
число вариант
Тогда
число вариант
![]() в
выборке равно …
в
выборке равно …
|
|
|
37 |
|
|
|
63 |
|
|
|
100 |
|
|
|
36 |
Тема: Системы линейных уравнений с комплексными коэффициентами Система решается матричным способом по формуле , где , – матрица свободных членов. Тогда матрица , обратная к матрице системы , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений Однородная система имеет только одно нулевое решение, если принимает значения не равные …
|
|
|
2 |
|
|
|
– 2 |
|
|
|
1 |
|
|
|
– 1 |
Тема: Базис и размерность линейного пространства Даны матрица перехода от старого базиса к новому и вектор с координатами в новом базисе. Тогда координаты вектора в старом базисе имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа Функция представлена таблицей Тогда значение , вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
6 |
Тема:
Числовые характеристики случайных
величин
Проводится
n
независимых испытаний, в каждом из
которых вероятность появления события
A
постоянна и равна 0,6. Тогда математическое
ожидание
![]() и
дисперсия
и
дисперсия
![]() дискретной
случайной величины X
– числа появлений события A
в
дискретной
случайной величины X
– числа появлений события A
в
![]() проведенных
испытаниях равны …
проведенных
испытаниях равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
|
Тема:
Численные методы решения дифференциальных
уравнений и систем
Методом
Эйлера решается задача Коши
![]() ,
с
шагом
.
Тогда значение искомой функции
в
точке
будет
равно …
,
с
шагом
.
Тогда значение искомой функции
в
точке
будет
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Плоскость в пространстве
Нормальное
уравнение плоскости
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Периодические функции
Основной
период функции
![]() равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Системы линейных уравнений
Система
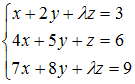 совместна,
если
равно …
совместна,
если
равно …
|
|
|
1 |
|
|
|
2 |
|
|
|
– 1 |
|
|
|
– 2 |
Тема:
Вычисление определителей
Определитель
 равен
…
равен
…
|
|
|
– 22 |
|
|
|
2 |
|
|
|
|
|
|
|
22 |
Тема: Умножение матриц Умножение матрицы A на матрицу B возможно, если эти матрицы имеют вид …
|
|
|
|
|
|
|
и
|
|
|
|
|
|
|
|
и
|
Тема:
Элементы теории множеств
Даны
множества:
![]() ,
,
![]() .
Тогда число целых чисел, принадлежащих
их объединению равно …
.
Тогда число целых чисел, принадлежащих
их объединению равно …
|
9 |
|
Тема:
Дифференцирование функции комплексного
переменного
Значение
производной функции
![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы теории множеств Даны три множества: , и . Тогда число элементов множества равно …
|
1
|
|
|
Тема: Числовые характеристики случайных величин Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее дисперсия равна …
|
Ошибка! Ошибка внедренного объекта. |
|
|
|
Ошибка! Ошибка внедренного объекта. |
|
|
|
Ошибка! Ошибка внедренного объекта. |
|
|
|
Ошибка! Ошибка внедренного объекта. |
|
|
Тема: Непрерывность функции, точки разрыва Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Тема: Дифференциальное исчисление ФНП Приближенное значение функции в точке , вычисленное с помощью полного дифференциала, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Основные методы интегрирования Множество первообразных функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тЕма:
Приложения определенного интеграла
Объем
тела, полученного вращением вокруг оси
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Прямая на плоскости
Прямые
![]() и
и
![]() пересекаются
в точке, лежащей на оси абсцисс. Тогда
эта точка имеет координаты …
пересекаются
в точке, лежащей на оси абсцисс. Тогда
эта точка имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Поверхности второго порядка Центр сферы имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямоугольные координаты на плоскости Даны точки и . Тогда координаты точки , симметричной точке относительно точки , равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Сходимость числовых рядов Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
|
|
|
ряд А) расходится, ряд В) расходится |
|
|
|
ряд А) сходится, ряд В) сходится |
|
|
|
ряд А) расходится, ряд В) сходится |
Тема: Числовые последовательности Числовая последовательность задана рекуррентным соотношением , , . Тогда равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
последовательно:
![]() ,
,
![]() .
.
Тема: Область сходимости степенного ряда Область сходимости степенного ряда имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Метрические пространства Расстояние между матрицами и в метрике равно …
|
|
|
43 |
|
|
|
13 |
|
|
|
2 |
|
|
|
34 |
Тема: Элементы теории множеств Даны три множества: , и . Тогда число элементов множества равно …
|
1 |
Тема: Отображение множеств Прообразом множества при отображении является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Мера плоского множества Плоская мера множества равна …
|
|
|
0 |
|
|
|
32 |
|
|
|
8 |
|
|
|
18 |
Тема: Градиент скалярного поля Модуль градиента скалярного поля в точке равен …
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
4 |
Тема: Норма вектора в евклидовом пространстве Даны векторы и , угол между которыми равен . Проекция вектора на вектор равна . Тогда норма вектора равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Векторное произведение векторов Площадь треугольника, образованного векторами и , равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Точечные оценки параметров распределения
Из
генеральной совокупности извлечена
выборка объема
![]() :
:
 Тогда
несмещенная оценка математического
ожидания равна …
Тогда
несмещенная оценка математического
ожидания равна …
|
|
|
13,14 |
|
|
|
13,0 |
|
|
|
13,34 |
|
|
|
13,2 |
Тема: Интервальные оценки параметров распределения Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Статистическое распределение выборки Из генеральной совокупности извлечена выборка объема : Тогда значение равно …
|
|
|
34 |
|
|
|
81 |
|
|
|
47 |
|
|
|
33 |
Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочный коэффициент корреляции может быть равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление Тригонометрическая форма записи комплексного числа имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами Система решается методом Крамера по формулам , . Тогда вспомогательный определитель равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного Значение производной функции в точке равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Законы распределения вероятностей дискретных случайных величин Дискретная случайная величина задана законом распределения вероятностей: Тогда ее функция распределения вероятностей имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Числовые характеристики случайных величин Дисперсия дискретной случайной величины , заданной законом распределения вероятностей: равна 0,06. Тогда значение равно …
|
|
|
1,5 |
|
|
|
0,5 |
|
|
|
3 |
|
|
|
6 |
Тема: Определение вероятности Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Полная вероятность. Формулы Байеса В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Типы дифференциальных уравнений Уравнение является …
|
|
|
уравнением с разделяющимися переменными |
|
|
|
линейным дифференциальным уравнением 1-го порядка |
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
|
|
|
уравнением Бернулли |
Тема: Однородные дифференциальные уравнения Общий интеграл дифференциального уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами Решение задачи Коши , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами Общее решение линейного однородного дифференциального уравнения второго порядка имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Базис и размерность линейного пространства Совокупность векторов , , не может являться базисом трехмерного линейного пространства, если равно …
|
|
|
2 |
|
|
|
4 |
|
|
|
1 |
|
|
|
3 |
Тема: Системы линейных уравнений Однородная система имеет только одно нулевое решение, если принимает значения не равные …
|
|
|
2 |
|
|
|
– 2 |
|
|
|
1 |
|
|
|
– 1 |
Тема: Умножение матриц Матрица , где и . Тогда элемент равен …
|
|
|
10 |
|
|
|
4 |
|
|
|
– 3 |
|
|
|
0 |
Тема: Вычисление определителей Определитель равен …
|
|
|
45 |
|
|
|
135 |
|
|
|
– 45 |
|
|
|
– 135 |
Тема: Интерполирование функций: интерполяционные полиномы Лагранжа Функция представлена таблицей Тогда значение , вычисленное с помощью интерполяционного многочлена Лагранжа, равно …
|
|
|
– 3 |
|
|
|
14 |
|
|
|
|
|
|
|
– 8 |
Тема: Численные методы решения дифференциальных уравнений и систем На отрезке задано дифференциальное уравнение . Значение производной второго порядка в точке может быть заменено выражением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Численное дифференцирование и интегрирование Значение определенного интеграла по формуле парабол (Симпсона) можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле Значение ряда Фурье функции в точке равно …
|
|
|
0 |
|
|
|
– 1 |
|
|
|
1 |
|
|
|
|
Тема: Элементы гармонического анализа Разложение функции на гармоники имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания Амплитуда гармонических колебаний равна ; угловая частота равна рад.; а начальная фаза равна . Тогда смещение колеблющейся точки от нулевого положения при составляет …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции Основной период функции равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление Тригонометрическая форма записи комплексного числа имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами Система решается методом Крамера по формулам , , . Тогда вспомогательный определитель равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|






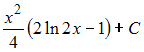








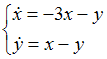 ,
,





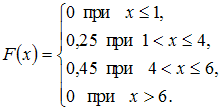





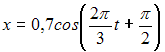


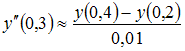
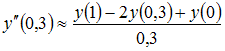


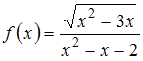

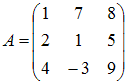 и
и

 и
и