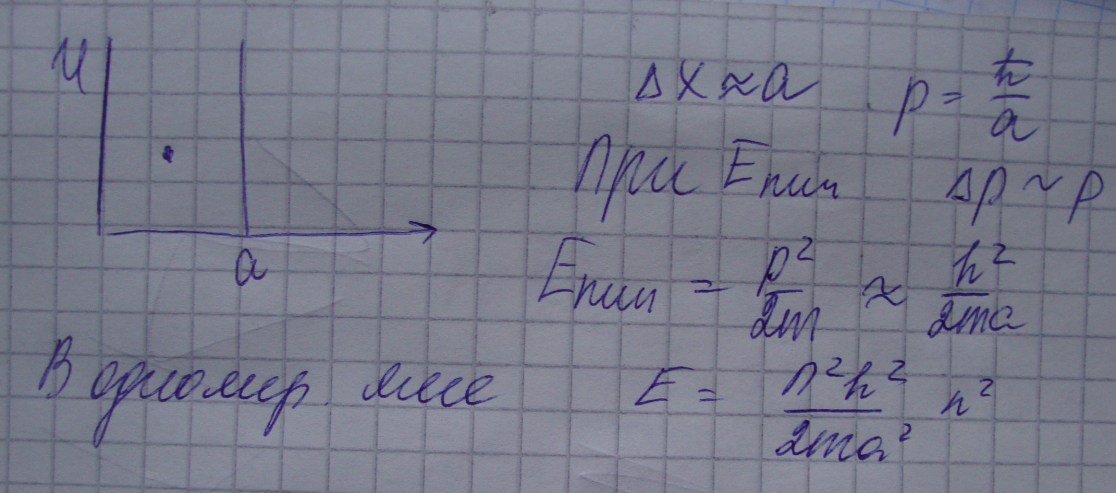Вопрос1. 1й постулат квантовой механики: состояние частицы в квантовой механике описывается волновой функцией ᵠ(X,y,z,t), являющейся функцией пространственных координат и времени.

2й постулат : каждой физической величине соответствует определённый оператор этой физической величины. При этом соотношение м/ду операторами в квантовой механике имеют ту же структуру, что и соотношение м/ду соответствующими им физическими величинами в классической механике.

3й постулат : в результате измерения физической величины f в любой квантовой системе могут быть получены только такие значения, которые являются собственными значениями оператора Ф, соответствующего этой величине.

Это важный постулат квантовой механики устанавливает связь м/ду теорией и возможностью её экспериментальной проверки.

4й постулат : Для расчёта среднего значения физической величины f в квантовом состоянии системы, описываемом волновой функцией ᵠ, окончательно получаем формулу <f>=∫ᵠ*(Фᵠ)dV.

Оператор координаты. Действие этого оператора на волновую функцию сводится к умножению её на соответствующую координату, т.е.

Оператор импульса. С помощью операций дифференцирования по координатам определим операторы проекций импульса, написав эти определения в символической операторной форме:

, используя оператор Лапласса:

Оператор момента импульса. Согласно формуле классической механики, определяющей момент импульса частицы как вектор L=r x p, запишем выражение для его проекции на координатной оси:

Опратор энергий. Классическая формула связи кинетической энергии частицы с квадратом её импульса Е_к=p² /(2m₀) позволяет записать аналогичное соотношение м/ду соответствующими операторами. Поэтому:

Если частица движется в стационарном силовом поле и её потенциальная энергия U=U(x,y,z) определена в любой точке пространства, то оператор потенциально функции определяется как оператор умножения функции U, т.е.

Так как полная энергия частицы в классической механике есть сумма кинетической и потенциальной энергии, то в квантовой механике оператор полной энергии H определяется как сумма операторов кинетической и потенциальной энергий. Поэтому

Представляя выражение для оператора квадрата импульса из формулы, запишем оператор полной энергии как

В классической механике полную энергию частицы, выраженную ч/з её координаты и импульсом, называют функцией Гамильтона. Поэтому в квантовой механике оператор полной энергии H назыюают функцией Гамильтона или просто гамильтолианом.

Гамильтон Н являтся основным оператором квантовой механики.

Вопрос3.

Задача2. Дано: r=0.1yv=0.1*10^-9м. V-? С помощью соотношения неопределённости

Решение: ∆x*∆p_x≥Ћ/2 ; ∆p_x=m∆v_x ; ∆x*∆v_x≥Ћ/2m; ∆x=r ; ∆v_x≥Ћ/2mr=1.054*10^-34/(2*9.1*10^-31*0.1*10^-9) = 0.579*10⁶ м/c

Ответ: 0,579*10⁶ м/с.

Билет 30

1) В квантовой физике вводится комплекснозначная функция , описывающая чистое состояние объекта, которая называется волновой функцией.

Гамильтониан H является основным оператором квантовой механики, поскольку, выбирая конкретный вид гамильтониана с учетом силового поля, действующего на частицу, мы формулируем на математическом языке все особенности квантовой системы. Поэтому и основное уравнение нерелятивистской квантовой механики – уравнение Шредингера – может быть записано в операторной форме, содержащей гамильтониан H:

Пример нерелятивистского уравнения Шрёдингера в координатном представлении для точечной частицы массы , движущейся в потенциальном поле c потенциалом  :

Согласно М. Борну, волновые функции  должны интерпре­тироваться статистически. На основании статистической интер­претации вероятность нахождения частицы в момент време­ни  с координатами х и x+dx, у и y+dy, z и z+dz определяется интенсивностью волновой функции, т. е. квадратом пси-функции. Поскольку в общем случае  — комплексная функция, а вероят­ность должна быть всегда действительной и положительной ве­личиной, то за меру интенсивности принимается квадрат модуля волновой функции

, где * — функция, комплексно сопряженная .

3) Теорию фотоэффекта создал немецкий ученый А. Эйнштейн в 1905 г. В основе теории Эйнштейна лежит понятие работы выхода электронов из металла и понятие о квантовом излучении света. По теории Эйнштейна фотоэффект имеет следующее объяснение: поглощая квант света, электрон приобретает энергии . При вылете из металла энергия каждого электро на уменьшается на определенную величину, котору называют работой выхода (  ). Работа выхода это работа, которую необходимо затратить, чтобы удалить электрон из металла. Поэтому максимальная кинетическая энергия электронов после вылета (если нет других потерь) равна: