2. Надбарьерное отражение

Этот термин употребляется, чтобы описать невозможное в классической физике явление отражения от потенциального барьера, высота которого меньше полной энергии частицы.

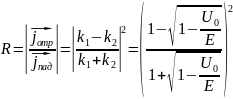
При 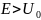существует отличная вероятность отражения частицы от низкого потенциального порога, этот результат является квантовым и объясняется наличием у частиц волновых свойств.

3. Исходя из того, что оператор азимутального угла имеет вид 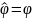, а оператор проекции момента импульса на ось 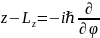, решить вопрос о возможности одновременного измерения в квантовой механике угла и проекции.

Возьмем одновр.измерения

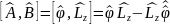
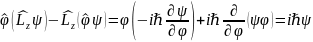
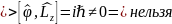
Билет 16.

1. Основные постулаты квантовой механики. Представление физических величин операторами. Гамильтониан квантовой системы как оператор полной энергии.

Постулат 1. О волновой функции.

Любое состояние системы полностью описывается некоторой функцией 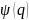от координат всех образующих систему частиц и времени.

Постулат 2. О способе описания физических величин.

Каждой динамической переменной ставится в соответствие самосопряженный оператор. Все отношения м/у величинами классики в квантовой заменяются отношениями м/у операторами.

Постулат 3. Об основном уравнении квантовой механики.

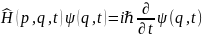
Постулат 4. О возможных значениях физических величин.

Единственно возможными значениями, которые могут быть получены при измерении динамической переменной , являются собственные значения 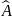операторного уравнения

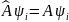
Постулат 5. О среднем значении физической величины.

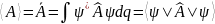
Постулат 6. Принцип суперпозиции.

Если система может находиться в состояниях, описываемых волновыми функциями, то она может находиться и в состоянии

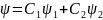
Постулат 7. Об антисимметричности волновой функции.

Волновая функция системы частиц с полуцелым спином должна быть антисимметрична относительно перестановки координат любых двух частиц:

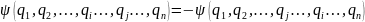
Гамильтониа́н ( H) в квантовой теории — оператор полной энергии системы

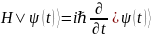
2. Красная граница фотоэффекта.

минимальная частота или максимальная длина волны света, при которой еще возможен внешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота зависит только от работы выхода электрона

3. Частица массы м находится в двумерной квадратной потенциальной яме с беск.высокими стенками. Сторона равна а. Найти значения энергии частицы для первых четырех уровней.

Билет 17.

1. Основные постулаты квантовой механики. Представление физических величин операторами. Гамильтониан квантовой системы как оператор полной энергии.

Постулат 1. О волновой функции.

Любое состояние системы полностью описывается некоторой функцией от координат всех образующих систему частиц и времени.

Постулат 2. О способе описания физических величин.

Каждой динамической переменной ставится в соответствие самосопряженный оператор. Все отношения м/у величинами классики в квантовой заменяются отношениями м/у операторами.

Постулат 3. Об основном уравнении квантовой механики.

Постулат 4. О возможных значениях физических величин.

Единственно возможными значениями, которые могут быть получены при измерении динамической переменной , являются собственные значения операторного уравнения

Постулат 5. О среднем значении физической величины.

Постулат 6. Принцип суперпозиции.

Если система может находиться в состояниях, описываемых волновыми функциями, то она может находиться и в состоянии

Постулат 7. Об антисимметричности волновой функции.

Волновая функция системы частиц с полуцелым спином должна быть антисимметрична относительно перестановки координат любых двух частиц:

Гамильтониа́н ( H) в квантовой теории — оператор полной энергии системы

Вероятностный смысл волновой функции. Квадрат модуля волновой функции (x,y,z,t) определяет плотность вероятности w того, что в момент времени t0 частица может быть обнаружена в точке пространства M=M(x,y,z) с координатами x, y и z.w=dP/dV=||²=*. Волновую функцию, удовлетворяющую условию нормировки _F||²dV=1, называют нормированной волновой функцией. Представление физических величин операторами. Вычисление средних значений физических величин.

А) Оператор координаты. Действие сводится к умножению волновой функции на эту координату: x^{^}=x, y^=y, z^=z или x^=x…

б) Оператор проекций импульса. Выражаются с помощью операторов дифференцирования по соответствующим координатам: P^_x=(h/i)(/x), P^_y=(h/i)(/y), P^_z=(h/i)(/z),­­­­­­p^={ P^_x, P^_y, P^_z}.

В) Оператор момента импульса:

L=rp, L_x=yp_z-zp_y; L_y=zp_y-xp_z; L_z=xp_y-yp_x;

L^_x=y^p^_z-z^p^_y=(h/i)(y/x-z/y).

Г) Оператор кинетической энергии. Определим T, пользуясь формулой Т=p²/2m, T^=p^²/2m=-h²/2m. Вычисление средних значений: L^=L,<L>=*L^dV, (r)=Aexp(-r/a)

Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии квантаэлектромагнитного излучения с его частотой так же, как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действия с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское  .

 Дж·c^[1]

Часто применяется величина  :

покажите, что в атоме водорода на круговой стационарной боровской орбите укладывается целое число длин волн де Бройля электрона. Определите длину волны де Бройля электрона на круговой орбите с главным квантовым числом n.

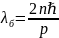
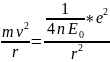
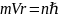
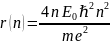
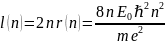
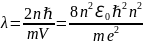
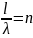
Билет 18.

Если для некоторого квантового состояния волновая функция ψ не является

JK

собственной функцией оператора Ф, то в этом квантовом состоянии физическая величина f не имеет определенного значения. Вероятность Рn того, что при измерении физической величины f в этом квантовом состоянии будет получено численное значение fn находится по формуле

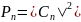^(Ы)

а среднее значение (математическое ожидание) физической величины по результатам большого числа измерений можно определить как

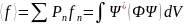
Необходимым и достаточным условием возможности одновременного точного

измерения двух физических величин а и h является коммутативность

соответствующих им операторов А и B , т. е. выполнение равенства

[A,В]= ВА-BA=0. (1-6)

Если же коммутатор [A,В] двух операторов не равен нулю, то соответствующие

им две физические величины не могут быть измерены одновременно точно. Для таких физических величин справедливы соотношения неопределенностей вид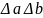 >0 утверждающие, что обе неопределенности 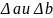не могут одновременно стремиться к нулю.

A a и A b не могут одновременно стремится к нулю. Принцип неопределенности Гейзенберга Своеобразие св-в микрочастиц - не для всех переменных получаются при измерениях опред. значения. Микрочастица не может иметь одновр.точных зн-ий

коорд. и импульса. Неопределенности зн-ий х и рхудовл. соотн.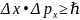

Произведение неопред, зн-ий двух сопряженных переменных не может быть по порядку величины оытъ меньше пост, планка. Для энергии имеем 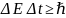(Для измер. энергии с погрешностью необх. время не меньшее чем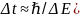

1. Энергетические величины. Поток излучения Ф_е— величина, равная отношению энергии W излучения ко времени t, за которое излучение произошло:

Единица потока излучения — ватт (Вт).

Энергетическая светимость (излучательность) R_e — величина, равная отношению потока излучения Ф_е; испускаемого поверхностью, к плошали S сечения, сквозь которое этот поток проходит:

т. е. представляет собой поверхностную плотность потока излучения.

Единица энергетической светимости — ватт на метр в квадрате (Вт/м²)

задача.

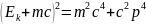
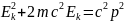
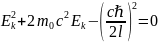
решая уравнение 2 коня, один отрицательный – не имеет смысла, следовательно ответ :

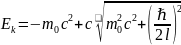
Билет 19.