
- •1. Ядерная модель атома. Постулаты Бора
- •2. Уравнение Энштейна для фотоэффекта, его физический смысл.
- •3. Испускательная способность тела , ее физический смысл.
- •Билет 11
- •Билет 12
- •Надбарьерное отражение
- •Красная граница фотоэффекта.
- •Стационарное уравнение Шредингера для атома водорода. Спектр атома водорода.
- •Надбарьерное отражение квантовой частицы, его физическая причина.
- •Тепловое излучение. Интегральные и спектральные характеристики излучения. Закон Кирхгофа. Закон Стефана-Больцмана. Закон смещения Вина.
- •Квантовые числа и их физический смысл.
- •Вопрос 2.
- •1.Корпускулярно-волновой дуализм материи. Гипотеза де Бройля. Опыты по дифракции микрочастиц.
- •Вопрос1. 1й постулат квантовой механики: состояние частицы в квантовой механике описывается волновой функцией ᵠ(X,y,z,t), являющейся функцией пространственных координат и времени.
- •Вопрос3.
Билет 1.
Тепловое излучение- ЭМ волны, испускаемые при температуре выше абсолютного нуля всеми телами за счет их внутренней энергии .
Спектральные характеристики рассматривают распределение энергии на различных частотах.
Интегральные хар-ки:
Энергия излучения W
Поток излучения (мощность)
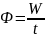 (Вт)
(Вт)Излучательность (энергетическая светимость) R- величина, равная потоку излучения, испускаемого с единицы площади тела по всем направлениям в полусферу.
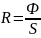
Лучистость (энергетическая яркость) поверхности .
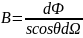
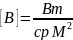
Спектральные хар-ки:
Спектр. Объемная плотность.
 .
Энергия излучения
.
Энергия излучения
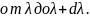
Спектр. Плотность энергетической светимости.
 .
А по всем длинам волн
.
А по всем длинам волн

Спектр. Коэф. Поглощения – отношение поглощенного потока излучения к падающему потоку излучения
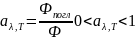
Закон
Кирхгофа: для всех тел отношение
испускательной способности к поглощательной
способности равно испускательной
способности абсолютно черного тела при
той же температуре и длине волны.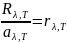 Не зависит от их формы и химической
природы.
Не зависит от их формы и химической
природы.
Закон
смещения Вина: Длина волны
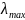 , соответствующая максимальной
спектральной плотности излучательности
АЧТ, обратно пропорционально температуре.
, соответствующая максимальной
спектральной плотности излучательности
АЧТ, обратно пропорционально температуре.

Закон
Стефана-Больцмана. Излучательность
АЧТ, т.е. полная мощность излучения с
единичной площади, пропорциональная
четвертой степени температуры.
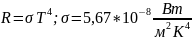
3)
Отношение квадратов амплитуд волн,
прошедшей в область и падающей на барьер,
показывает коэф. Прозрачности.
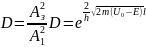 .
Физический смысл: вероятность прохождения
частицы через потенциальный барьер из
области 1 в область 2. Это вероятность
не равна 0, даже когда энергия частицы
меньше энергии барьера.
.
Физический смысл: вероятность прохождения
частицы через потенциальный барьер из
области 1 в область 2. Это вероятность
не равна 0, даже когда энергия частицы
меньше энергии барьера.
2)
Частица находится в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками в состоянии,
описываемом квантовым числом n.
Найдите среднее значение квадрата
импульса частицы
 в этом состоянии.
в этом состоянии.
Решение:

Билет 2.
ЭМ волна при поглощении и излучении может минимально дробиться только на порции по
 .
Формула Планка для плотности энергии
излучения.
.
Формула Планка для плотности энергии
излучения.
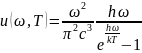
Гипотеза
Планка. Э.М. излучение испускается и
поглощается в виде отдельных порций
энергии (квантов)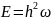 . Из принципа детального равновесия
следует, что возбуждены будут все уровни
энергии с различной вероятностью.
Вероятность n-ого уровня
. Из принципа детального равновесия
следует, что возбуждены будут все уровни
энергии с различной вероятностью.
Вероятность n-ого уровня
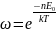 ,
среднее значение энергии
,
среднее значение энергии
3)Система, полная энергия к-рой определяется заданием оператора Я (гамильтониана), может иметь т стационарных состояний, для к-рых ур-ние Шрёдингера [Шредингера] определяет соответствующие волновые ф-ции(i = 1, 2, ..., т)и одно значение энергии Е, одинаковое для всех т состояний. Энергетический уровень квантовой системы называется вырожденным, если содержит более одного состояния. Говоря математически, соответствующее значение энергии является кратным собственным значением гамильтониана. Количество независимых таких состояний (то есть кратность собственного значения) называется кратностью вырождения.
2)Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками во втором возбужденном состоянии. Какова вероятность нахождения частицы в средней трети ямы?
Решение:

Билет 3.
№1 Фотоэффект - явление испускания электронов под действием света или УФ излучения.
З![]() аконы
фотоэффекта. 1)кол-во испускаемых за ед
времени электронов пропорционально
интенсивности излучения. 2)для каждого
вещества существует мин. частота или
макс длина волны (красная граница
фотоэффекта) за которой фотоэффект
отсутствует. 3) макс. кинетическая
энергия испущенных электронов линейно
возрастает с увеличением частоты
излучения и не зависит от его интенсивности.
аконы
фотоэффекта. 1)кол-во испускаемых за ед
времени электронов пропорционально
интенсивности излучения. 2)для каждого
вещества существует мин. частота или
макс длина волны (красная граница
фотоэффекта) за которой фотоэффект
отсутствует. 3) макс. кинетическая
энергия испущенных электронов линейно
возрастает с увеличением частоты
излучения и не зависит от его интенсивности.
уравнение Эйнштейна для фотоэффекта. Работа выхода- минимальная энергия сообщаемая электрону для выхода с поверхности метала
Такие явления как интерференция и дифракция свидетельствуют о волновой природе света. Фотоэффект свидетельствует о том, что свет является потоком частиц(корпускул). Т.е. свет обнаруживает корпускулярно-волновой дуализм.
№2

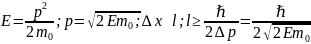 №3 Как
следует из решения уравнения Шредингера
для атома водорода, квантовое состояние
электрона полностью определяется
заданием трех квантовых чисел.
№3 Как
следует из решения уравнения Шредингера
для атома водорода, квантовое состояние
электрона полностью определяется
заданием трех квантовых чисел.
Число n определяет значение электрона в атоме и называется главным квантовым числом n=1,2,3...
Число l определяет величину момента импульса электрона, называется орбитальным квантовым числом. l=0,1,....(n-1)
Число m называется магнитным квантовым числом. Оно определяет проекцию момента импульса на ось вращения. m=-l,....,0,....l
Билет 4.
№1
Эффект
Комптона.- явление, состоящее в изменении
длины волны рассеянного излучения при
пропускании через вещество рентгеновского
диапазона. Изменение длины волны не
зависит от свойств вещества, но зависит
от угла рассеяния. если длина волны
падающего излучения 𝜆,
длины волны рассеянного 𝜆',
θ- угол рассеяния, то справедлива формула
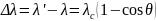 ,
где
,
где
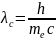 -постоянная
величина(комптоновская постоянная)
-постоянная
величина(комптоновская постоянная)
Такие явления как интерференция и дифракция свидетельствуют о волновой природе света. Фотоэффект свидетельствует о том, что свет является потоком частиц(корпускул). Т.е. свет обнаруживает корпускулярно-волновой дуализм.
№2
nx |
ny |
nz |
E |
выр |
1 |
1 |
1 |
3с (1ур) |
1 |
1 |
1 |
2 |
6с(2ур) |
3 |
1 |
2 |
2 |
9с(3ур) |
3 |
2 |
2 |
2 |
12с (5ур) |
1 |
1 |
1 |
3 |
11с (4ур) |
3 |

кратность вырождения 3 уровня =3
№3
Энергия ионизации наименьшая энергия, необходимая для удаления электрона от свободного атома в его низшем энергетическом (основном) состоянии на бесконечность. Энергия ионизации атома зависит от его электронной конфигурации. В частности, завершенные электронные слои обнаруживают повышенную устойчивость
Билет 5.
1. Ядерная модель атома. Постулаты Бора
Резерфорд предложил, что атом устроен подобно планетарной системе. Суть модели строения атома по Резерфорду заключается в следующем: в центре атома находится положительно заряженное ядро, в котором сосредоточена вся масса, вокруг ядра по круговым орбитам на больших орбитах вращаются электроны (как планеты вокруг солнца). Заряд ядра совпадает с номером химического элемента в системе Менделеева.
Постулаты Бора: 1. Атом может находится в определенных стационарных состояниях (квантовых). В них атом не излучает электромагнитных волн. 2. Электрон в атоме, не теряя энергии, движется по определенным стационарным орбитам, причем момент импульса зависит от номера орбиты и определяется формулой: mVnrn=nh, n – номер орбиты. 3. При переходе электрона с орбиты на орбиту он либо излучает энергию, либо поглощает ее (фотон). С более высокой орбиты на более низкую он теряет Е, в обратном случает получает: Энергия излучения: hω=En-Em
2. Уравнение Энштейна для фотоэффекта, его физический смысл.
Уравнение
Энштейна: hν=Aвых+ Смысл:
энергия кванта тратится на работу выхода
электрона из металла и сообщении ему
кинетической энергии.
Смысл:
энергия кванта тратится на работу выхода
электрона из металла и сообщении ему
кинетической энергии.
Задача
U=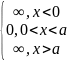 Внутри
ямы
Внутри
ямы
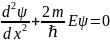 K=
K=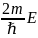 n
n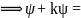 ;
;
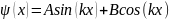 ;
Bcos(kx)=0;
;
Bcos(kx)=0;
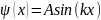 ;
;
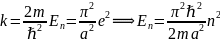

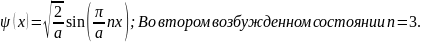
 ;
;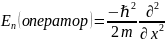 (оператор кинетической энергии)
(оператор кинетической энергии)
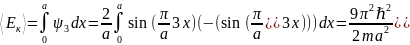
Билет 6.
1. Корпускулярно-волновой дуализм материи. Теория де Бройля. Опыты, подтверждающие наличие волновых свойств у микрочастиц. Корпускулярно волновой дуализм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантовых полей и квантовой теории поля.
Как классический пример, свет можно трактовать как поток корпускул (фотонов), которые во многих физических эффектах проявляют свойства электромагнитных. Свет демонстрирует свойства волны в явлениях дифракции и интерференции при масштабах, сравнимых с длиной световой волны. Например, даже одиночные фотоны, проходящие через двойную щель, создают на экране интерференционную картину, определяемую уравнениями Максвела.
Гипотеза
де Бройля: Де Бройль поставил в соответствие
движения микрочастиц - некоторый
волновой процесс
 ,
,
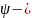 какая-то
характеристика волны. Энергия фотона
какая-то
характеристика волны. Энергия фотона
 ,
импульс
,
импульс
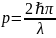 .
По
идее де Бройля движение электрона или
какой-либо другой частиц связано с
волновым процессом, длина волны которого
равна
.
По
идее де Бройля движение электрона или
какой-либо другой частиц связано с
волновым процессом, длина волны которого
равна
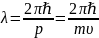 ,
а частота
,
а частота
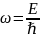 .
Экспериментальная
проверка гипотезы де Бройля: Дэвисон и
Джермер (1927) отражение электронов от
монокристала никеля, в результате
образуется дифракционная картина.
Томпсон получил дифракционную картину
при прохождении электронного пучка
через тонкую металлическую фольгу и
попадающего на фотопластину.
.
Экспериментальная
проверка гипотезы де Бройля: Дэвисон и
Джермер (1927) отражение электронов от
монокристала никеля, в результате
образуется дифракционная картина.
Томпсон получил дифракционную картину
при прохождении электронного пучка
через тонкую металлическую фольгу и
попадающего на фотопластину.
3. Испускательная способность тела , ее физический смысл.
Спектральной
испускательной способностью тела
(спектральной плотностью энергетической
светимости) называется физическая
величина, равная отношению мощности
излучения dRω
для волн с частотами в диапазоне (ω ,ω+
dω
) к величине этого диапазона
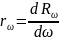 ⋅
Следовательно, если известна функция
спектральной испускательной способности,
то можно получить энергетическую
светимость
⋅
Следовательно, если известна функция
спектральной испускательной способности,
то можно получить энергетическую
светимость
 .
Поэтому энергетическую светимость
называют также интегральной испускательной
способностью. Т.к. тепловое излучение
осуществляется за счёт внутренней
энергии, то мощность излучения зависит
от температуры тела, поэтому спектральная
светимость является функцией двухпараметров
– частоты и температуры, что подчёркивают
соответствующими обозначениями
.
Поэтому энергетическую светимость
называют также интегральной испускательной
способностью. Т.к. тепловое излучение
осуществляется за счёт внутренней
энергии, то мощность излучения зависит
от температуры тела, поэтому спектральная
светимость является функцией двухпараметров
– частоты и температуры, что подчёркивают
соответствующими обозначениями
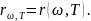 Тогда
RТ=
Тогда
RТ=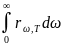 .
.
Задача
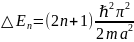


Билет 7.
1)Состояние
частицы в квантовой механике описывается
волновой
функцией
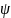 (x,y,z,t),
являющейся функцией пространственных
координат и времени.
(x,y,z,t),
являющейся функцией пространственных
координат и времени.
Статический
(вероятностный) смысл волновой ф-ции:
квадрат модуля волновой ф-ции
(x,y,z,t)
определяет плотность вероятности
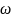 того, что в момент времени t>=
0 частица может быть обнаружена в точке
пространства М=М(x,y,z).т
е
того, что в момент времени t>=
0 частица может быть обнаружена в точке
пространства М=М(x,y,z).т
е
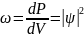 , dP=
, dP=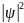 dV=
*
dV,
где dP
вероятность того, что для заданного
квантового состояния частиц в некоторый
момент времени мы обнаружим частицу в
элементарном объёме dV,
окружающем точку М. Можно так же рассчитать
вероятность Р того, что частица будет
обнаружена в любой области пространства
конечного объёма V.
dV=
*
dV,
где dP
вероятность того, что для заданного
квантового состояния частиц в некоторый
момент времени мы обнаружим частицу в
элементарном объёме dV,
окружающем точку М. Можно так же рассчитать
вероятность Р того, что частица будет
обнаружена в любой области пространства
конечного объёма V.
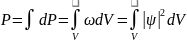 или
или
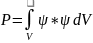 .
.
Условия регулярности волновой функции. 1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких что интегалы (см выше) станут расходящимися интегралами. 2. Условие однозначности волновой ф-ции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определиться в каждой задаче однозначно. 3. Условие непрерывности волновой ф-ции. В любой момент времени волновая ф-ция и её частные производные должна быть непрерывной ф-цией пространственных координат.
Принцип
суперпозиции в квантовой механике. Если
частица может находиться в квантовом
состоянии, описываемом волновой функцией
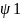 ,
а также в другом квантовом состоянии,
описываемом волновой функцией
,
а также в другом квантовом состоянии,
описываемом волновой функцией
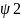 ,
то эта частица может находиться в
состоянии, описываемом волновой функцией
,
то эта частица может находиться в
состоянии, описываемом волновой функцией
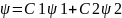 ,
т е существует квантовое состояние
частицы, описываемое волновой ф-цией
,
т е существует квантовое состояние
частицы, описываемое волновой ф-цией
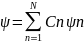 , где Сn-вероятность
нахождения частицы в квантовом состоянии
, где Сn-вероятность
нахождения частицы в квантовом состоянии
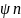 .
.
2) R*=
R*=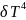 T=
T=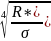 ,
,

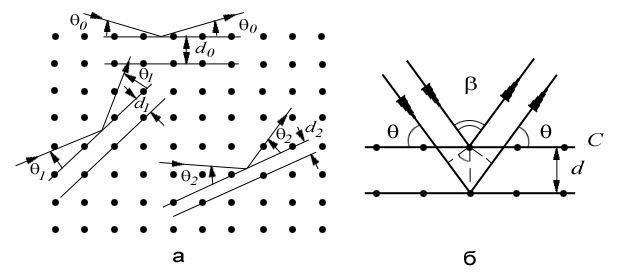 3)
Физический
смысл условия Брэгга-Вульфа. Рассмотрим дифракцию
электронов на совершенном кристалле,
т.е. кристалле, обладающем идеальной,
без каких-либо нарушений кристаллической
решеткой. Пусть электроны падают на
кристалл под углом скольжения
3)
Физический
смысл условия Брэгга-Вульфа. Рассмотрим дифракцию
электронов на совершенном кристалле,
т.е. кристалле, обладающем идеальной,
без каких-либо нарушений кристаллической
решеткой. Пусть электроны падают на
кристалл под углом скольжения 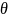 по
отношению к рассеивающему семейству
плоскостей. Тогда угол
будет
углом скольжения, под которым электроны
падают на поверхность кристалла, а
угол
по
отношению к рассеивающему семейству
плоскостей. Тогда угол
будет
углом скольжения, под которым электроны
падают на поверхность кристалла, а
угол 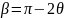 -
углом между падающим и дифрагировавшим
пучками электронов. При
значении угла
,
удовлетворяющем условию
Брэгга-Вульфа
-
углом между падающим и дифрагировавшим
пучками электронов. При
значении угла
,
удовлетворяющем условию
Брэгга-Вульфа
 возникает
интенсивный дифракционный максимум
отраженной волны. Здесь
возникает
интенсивный дифракционный максимум
отраженной волны. Здесь ![]() -
брэгговский угол,
-
брэгговский угол, ![]() -
расстояние между отражающими плоскостями
(постоянная решетки кристалла),
-
расстояние между отражающими плоскостями
(постоянная решетки кристалла), ![]() -
целое число, принимающее значения 1, 2,
3, ... , называемое порядком отражения.
Физический смысл условия Брэгга-Вульфа :
дифракционный максимум появляется в
тех случаях, когда разность хода волн,
отраженных от соседних атомных плоскостей,
равна целому числу длин волн де Бройля.
Именно в этом случае отраженные волны
усиливают друг друга, т.е. имеет место
конструктивная интерференция.
-
целое число, принимающее значения 1, 2,
3, ... , называемое порядком отражения.
Физический смысл условия Брэгга-Вульфа :
дифракционный максимум появляется в
тех случаях, когда разность хода волн,
отраженных от соседних атомных плоскостей,
равна целому числу длин волн де Бройля.
Именно в этом случае отраженные волны
усиливают друг друга, т.е. имеет место
конструктивная интерференция.
Билет 8.
1) Первый постулат : Состояние частицы в квантовой механике описывается волновой функцией (x,y,z,t), являющейся функцией пространственных координат и времени. Второй постулат: Каждой физич величине соответствует определённый оператор этой физич величины. (Оператор-это математ правило, следуя которому можно преобразовать одну функцию в другую)
1.Оператор координаты.
Действие
этого оператора на волновую функцию
сводится к умножению ее на соответствующую
координату, то есть.
![]() В символической операторной форме
записи этих операций имеют вид.
В символической операторной форме
записи этих операций имеют вид.
![]() Объединяя эти формулы, можно ввести
векторный оператор
Объединяя эти формулы, можно ввести
векторный оператор ![]() ,
соответствующий радиусу-вектору
,
соответствующий радиусу-вектору ![]() в
классической механике. Такой оператор
формально рассматривается как некоторый
вектор, имеющий в качестве компонент в
декартовой системе координат операторы
в
классической механике. Такой оператор
формально рассматривается как некоторый
вектор, имеющий в качестве компонент в
декартовой системе координат операторы ![]() .
Поэтому
.
Поэтому
![]()
2.Оператор
импульса. С помощью операций
дифференцирования по координатам
определим операторы проекций импульса,
записав эти определения в символической
операторной форме как
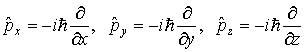 ,
можно объединить
,
можно объединить
![]() ,
,
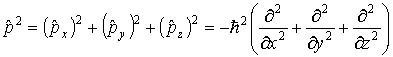 ,
,
![]() .
.
 3.Оператор
момента импульса.
По
формуле классической механики,
определяющей момент импульса частицы
как вектор
3.Оператор
момента импульса.
По
формуле классической механики,
определяющей момент импульса частицы
как вектор ![]() ,
запишем выражения для его проекций на
координатные оси:
,
запишем выражения для его проекций на
координатные оси:
![]() .
Операторные,
определяющие операторы проекций момента
импульса и оператор квадрата момента
импульса.
.
Операторные,
определяющие операторы проекций момента
импульса и оператор квадрата момента
импульса.
![]()
Где
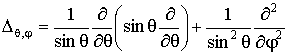
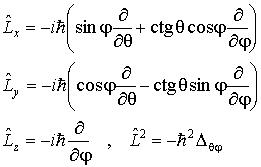 .
.
3.Оператор энергии.
Классическая
формула связи кинетической энергии
частицы с квадратом ее импульса
 позволяет
записать соотношение между соответствующими
операторами
позволяет
записать соотношение между соответствующими
операторами
 Если частица движется в стационарном
силовом поле, и ее потенциальная энергия
U=U(x,y,z)
определена в любой точке пространства,
то оператор потенциальной энергии
Если частица движется в стационарном
силовом поле, и ее потенциальная энергия
U=U(x,y,z)
определена в любой точке пространства,
то оператор потенциальной энергии
![]() .
Полная энергия частицы
.
Полная энергия частицы
 ,
,
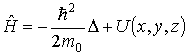 .
.
Третий
постулат:
что
в результате измерений физической
величины ![]() в
любой квантовой системе могут быть
получены только такие значения, которые
являются собственными значениями
соответствующего оператора
в
любой квантовой системе могут быть
получены только такие значения, которые
являются собственными значениями
соответствующего оператора![]() .
Он устанавливает связь между теорией
и возможностью ее эксперементальной
проверки.
.
Он устанавливает связь между теорией
и возможностью ее эксперементальной
проверки.
![]() ,
,
![]() ,
формула
для расчета среднего значения физической
величины
в
квантовом состоянии системы, описываемом
волновой функцией
,
формула
для расчета среднего значения физической
величины
в
квантовом состоянии системы, описываемом
волновой функцией ![]() :
:
![]() -
четвёртый
постулат.
-
четвёртый
постулат.
![]() .
.
2)
 ,
условие Брэгга-Вульфа:
,
условие Брэгга-Вульфа:
 ,
n=1,
,
n=1,
 ,
,
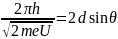 ,
,
 ,
,
 .
.
Если в качестве области пространства в P=
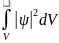 или
взять
все пространство
или
взять
все пространство  ,
для которого
,
для которого 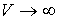 ,
то обнаружение частицы во всем
пространстве является достоверным
событием, вероятность которого равна
единице. Следовательно, из вероятностного
смысла волновой функции вытекает, что
,
то обнаружение частицы во всем
пространстве является достоверным
событием, вероятность которого равна
единице. Следовательно, из вероятностного
смысла волновой функции вытекает, что
 или
или
 (1) . Эти условия называют
условием нормировки волновой функции,
а волновую функцию, удовлетворяющую
этому условию, называют нормированной
волновой функцией. в некоторых задачах
квантовой механики условие нормировки
в виде (1) может
не выполняться. В таких задачах частица
движется из бесконечности и уходит в
бесконечность. Поэтому квадрат модуля
волновой функции в таких задачах не
стремится к нулю на бесконечности, и
интеграл в условии (1) становится
расходящимся. Примером такой волновой
функции служит плоская волна де Бройля
(1) . Эти условия называют
условием нормировки волновой функции,
а волновую функцию, удовлетворяющую
этому условию, называют нормированной
волновой функцией. в некоторых задачах
квантовой механики условие нормировки
в виде (1) может
не выполняться. В таких задачах частица
движется из бесконечности и уходит в
бесконечность. Поэтому квадрат модуля
волновой функции в таких задачах не
стремится к нулю на бесконечности, и
интеграл в условии (1) становится
расходящимся. Примером такой волновой
функции служит плоская волна де Бройля 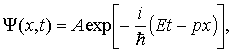 ,
которая является волновой функцией,
описывающей квантовое состояние
свободно движущейся частицы.
,
которая является волновой функцией,
описывающей квантовое состояние
свободно движущейся частицы.
Билет № 9
Уравнение Шредингера и его свойства. Статистическая интерпретация волновой функции.
Состояние микрочастицы, характеристики её движения, взаимодействия с другими частицами и т.д. полностью задаётся функцией, которую называют волновой функцией и обозначают Ψ (пси-функция).
Волновая функция должна являться решением уравнения Шрёдингера
iћ (/t)= - (ћ2/2m)* + U* (1);
где m – масса частицы, U – действительная функция координат и времени, такая, что вектор−gradU является классическим аналогом силы, действующей на частицу. В случае, когда U не зависит от времени, она совпадает с потенциальной энергией.
i2=-1; = (2/x2) + (2/y2) + (2/z2) - результат действия на функцию Ψ оператора Лапласа.
Уравнение (1) так же носит название (временное) уравнение Шредингера. Уравнение Шрёдингера является линейным, т.е. линейная комбинация решений тоже является решением. Принцип суперпозиции состояний не противоречит уравнению Шрёдингера.
Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость Y от времени, иными словами, найти уравнение Шредингера для стационарных состояний - состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частила движется, стационарно, т. е. функция U = U(х, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде
( x,y,z,t) = ѱ(x,y,z) e –i(E/ћ)t , или
ѱ + (2m/ћ2)(E-U)ѱ=0.
dP - вероятность того , что частица находится в некоторой малой области пространства, объём которой dV, определяется равенством
dP ||2dV
т.е. квадрат модуля волновой функции равен плотности вероятности нахождения частицы в некоторой области пространства (dP/dV)=||2. Поэтому для нахождения вероятности того, что частица находится в некоторой области V надо вычислить интеграл
P(V)=∫| |2dV=0.
2 задача.
Дано:
Абсолютно черное тело,
а) 3 К, б) 300 К,в) 3000 К, г) 5000 К
Найти: λm
Решение: λm=b/T,
b=2,90*10-3м * К;
λm1=2,90*10-3м * К/ 3 К=0.97*10-3м(далекая инфракрасная область, ограниченная с микроволновым диапазоном);
λm2=2,90*10-3м * К/300К=0,0097 *10-3 м(инфракрасная область);
λm3=2,90*10-3м * К/3000К=970нм(близкая инфракрасная область);
λm4=2,90*10-3м * К/5000К=580нм(видимая часть спектра).
Задание 3
Энергети́ческая
свети́мость ![]() — физическая
величина,
одна из энергетических
фотометрических
величин.
Характеризует мощность оптического
излучения,
излучаемого малым участком поверхности
единичной площади. Равна отношению потока
излучения
— физическая
величина,
одна из энергетических
фотометрических
величин.
Характеризует мощность оптического
излучения,
излучаемого малым участком поверхности
единичной площади. Равна отношению потока
излучения ![]() ,
испускаемого малым участком поверхности
источника излучения, к его площади
,
испускаемого малым участком поверхности
источника излучения, к его площади ![]() :
:
= / ; Численно энергетическая светимость равна среднему по времени модулю составляющей вектора Пойнтинга, перпендикулярной поверхности. Усреднение при этом проводится за время, существенно превосходящее период электромагнитных колебаний. [Вт.м−2]
Билет №10
Стационарные состояния, их временная зависимость. Уравнение Шредингера для стационарных состояний.
Состояния частицы, для которых значение энергии определено однозначно, называются
стационарными состояниями.
Волновая функции частицы в стационарном состоянии со значением энергии Е принимает особый вид Ψ( x,y,z,t) = ѱ(x,y,z) e –i(E/ћ)t, где функция «пси малая» ψ зависит только от координат частицы, но не зависит от времени, поэтому её иногда называют координатной частью волновой функции стационарного состояния. В стационарном состоянии плотность вероятности не зависит от времени. Действительно, плотность вероятности равна квадрату модуля волновой функции
|Ψ|2=| ѱ *e –i(E/ћ)t |2=| ѱ|2*| e –i(E/ћ)t|2=| ѱ|2
Следовательно, для стационарного состояния уравнение непрерывности для вероятности
примет вид: div (j) = 0/
Соответственно, вектор плотности вероятности для стационарного состояния имеет вид:
j=(iћ/2m)(ψ gradѱ*-ѱ*gradѱ)/
Уравнение Шрёдингера для стационарного состояния.
Необходимым условием стационарности состояния является независимость от времени
функции U, т.е. в стационарном состоянии эта функция однозначно трактуется как потенциальная энергия. В этом случае, подставим во временное уравнение Шрёдингера = ѱ * e –i(E/ћ)t ; ѱ + (2m/ћ2)(E-U)ѱ=0.
3 задание.
Уравнение Эйнштейна для фотоэффекта, его физический смысл.
Фотоэлектрическим эффектом или внешним фотоэффектом называется явление испускания электронов металлами под действием падающего света. (Явление испускания электронов веществом под действием падающего света называется фотоэмиссией).
А.Эйнштейн в 1905 г. построил теорию фотоэффекта (за эту работу он получил Нобелевскую премию по физике). Он предположил, что электромагнитное излучение не только испускается квантами, но поглощается тоже квантами. Тогда по закону сохранения энергии ћω=Ав+Екин_мах или hν= Ав+Екин_мах, т.е. энергия поглощённого кванта энергии расходуется на совершение электроном работы по выходу из металла (величина АВ называется работой выхода из металла) и на сообщение электрону кинетической энергии движения. Величина работы выхода АВ – это минимальная величина энергии, затрачиваемая на выход электрона из металла. В этом случае электрон приобретает максимальную кинетическую энергию ЕКИН_МАХ. В других случаях возможна ситуация, при которой электрону понадобится затратить больше энергии для выхода, поэтому и его кинетическая энергия будет меньше максимальной.
Законы фотоэффекта:
Формулировка 1-го закона фотоэффекта: Сила фототока прямо пропорциональна плотности светового потока.
Согласно 2-му закону фотоэффекта, максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.
3-й
закон фотоэффекта: для
каждого вещества существует красная
граница фотоэффекта, то есть минимальная
частота света ![]() (или
максимальная длина волны λ0),
при которой ещё возможен фотоэффект, и
если
(или
максимальная длина волны λ0),
при которой ещё возможен фотоэффект, и
если ![]() ,
то фотоэффект уже не происходит.
,
то фотоэффект уже не происходит.
