2.4. Сферические зеркала

В геодезии сферические зеркала стали применять сравнитель­но недавно — с появлением зеркально-линзовых зрительных труб. Сферические зеркала бывают вогнутые и выпуклые. От­метим, что закон отражения от плоского зеркала справедлив для малых элементов сферических зеркал, необходимо только перпен­дикуляром к поверхности элемента зеркала в точке падения луча считать нормаль к поверхности.

Рассмотрим вогнутое зеркало. Прямая, проходящая через центр кривизны зеркала С и центральную точку (вершину) зеркальной поверхности О, — главная ось зеркала (рис 8, а) - Луч S, идущий параллельно главной оси и имеющий угол падения i₁, отразится под углом i΄₁, равным по модулю углу падения i₁, но противоположным по знаку, а затем пройдет через точку F — фокус зеркала. Расстояние от фокуса F до вершины 0 называют фокусным и обозначают f. Если R — радиус кривизны зеркала, то

f = R/2 (24)

Угол между радиусами, проведенными из центра кривизны зеркала к его краям, – отверстный угол зеркала (рис. 8, б).

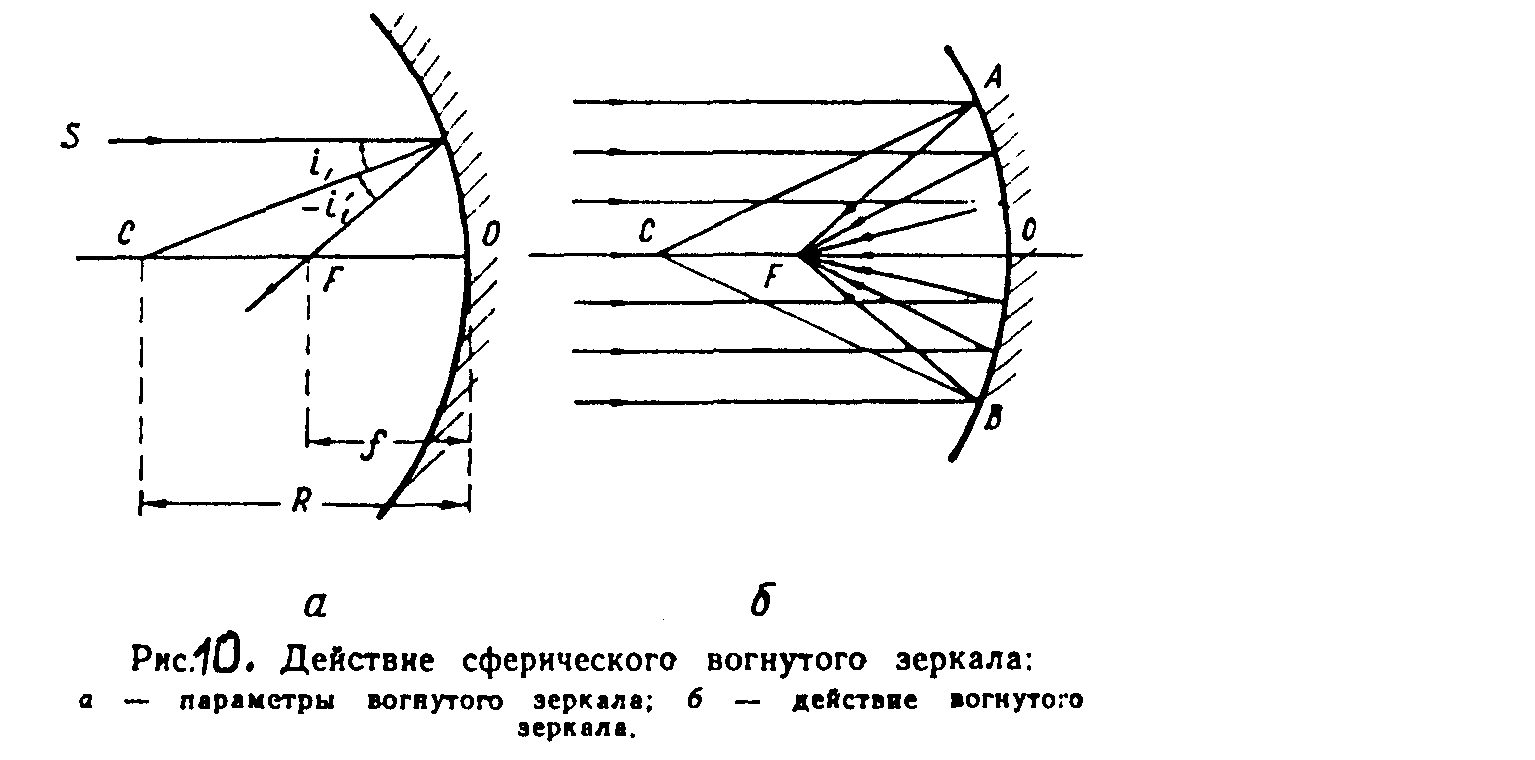
Рис.8. Действие сферического вогнутого зеркала:

а – параметры вогнутого зеркала;

б – действие вогнутого зеркала.

Все лучи, идущие к зеркалу параллельно его главной оси, после отражения соберутся в фокус F, и, наоборот, все лучи, проходящие через фокус F вогнутого сферического зеркала, после отражения пойдут параллельно его главной оси.

2.5. Линзы

Кусок прозрачного стекла с правильными большей частью сферическими поверхностями называют линзой. Линзы бывают двояковыпуклые, плосковыпуклые, вогнуто-выпуклые, двояковогнутые, плосковогнутые и выпукло-вогнутые.

Рис. 9. Типы линз

Первые три типа линз называются собирательными, т. к. световые лучи после прохождения через них сближаются по сравнению со своими начальными направлениями. Вторые три – рассеивающими, потому что лучи после прохождения через линзы удаляются друг от друга.

Лупа представляет собой двояковыпуклую линзу со сферическими поверхностями с центрами С₁ и С₂.

О

С₂

С₁

Линия, соединяющая центры С₁ и С₂ называется главной оптической осью линзы, а точка О оптическим центром линзы. Параллельные лучи, падающие на поверхность линзы после преломления, пересекают главную оптическую ось в одной точке, называемую главным фокусом. Расстояние от главного фокуса до оптического центра О называется фокусным расстоянием. Плоскости, проходящие через фокусы линзы и перпендикулярные к оптической оси, называются фокальными плоскостями. Лучи, проходящие через центр линзы, практически не преломляются.

В геодезических инструментах лупа предназначена для рассмотрения мелких штрихов лимба и верньера. Ход лучей можно видеть на рисунке. Наблюдаемый предмет ав от линзы находится на расстоянии меньше фокусного. Возьмем два луча, исходящие из точки а, один аm, параллелен оптической оси, другой аО, проходящий через оптический центр О. Для глаза они дадут изображение в точке А. Аналогично этому лучи, исходящие из точки в, дадут изображение в точке В. Таким образом АВ будет изображением рассматриваемого предмета ав. Это изображение мнимое, прямое, увеличенное. В лупу глаз видит изображение АВ под углом β=АОВ, а простым глазом тот же предмет виден под углом, α=а₀Ов₀. Отношение указанных углов есть увеличение лупы.

(25)

Увеличение можно выразить отношением длин АВ:а₀в₀=АВ:ав. С учетом подобия треугольников Fmn и FАВ V= или (26)

D – расстояние наилучшего зрения, l – расстояние глаза до линзы. Лупа с коротким фокусом дает большее увеличение. Отбросим , тогда увеличение прямо пропорционально расстоянию D и обратно пропорционально фокусному расстоянию f.

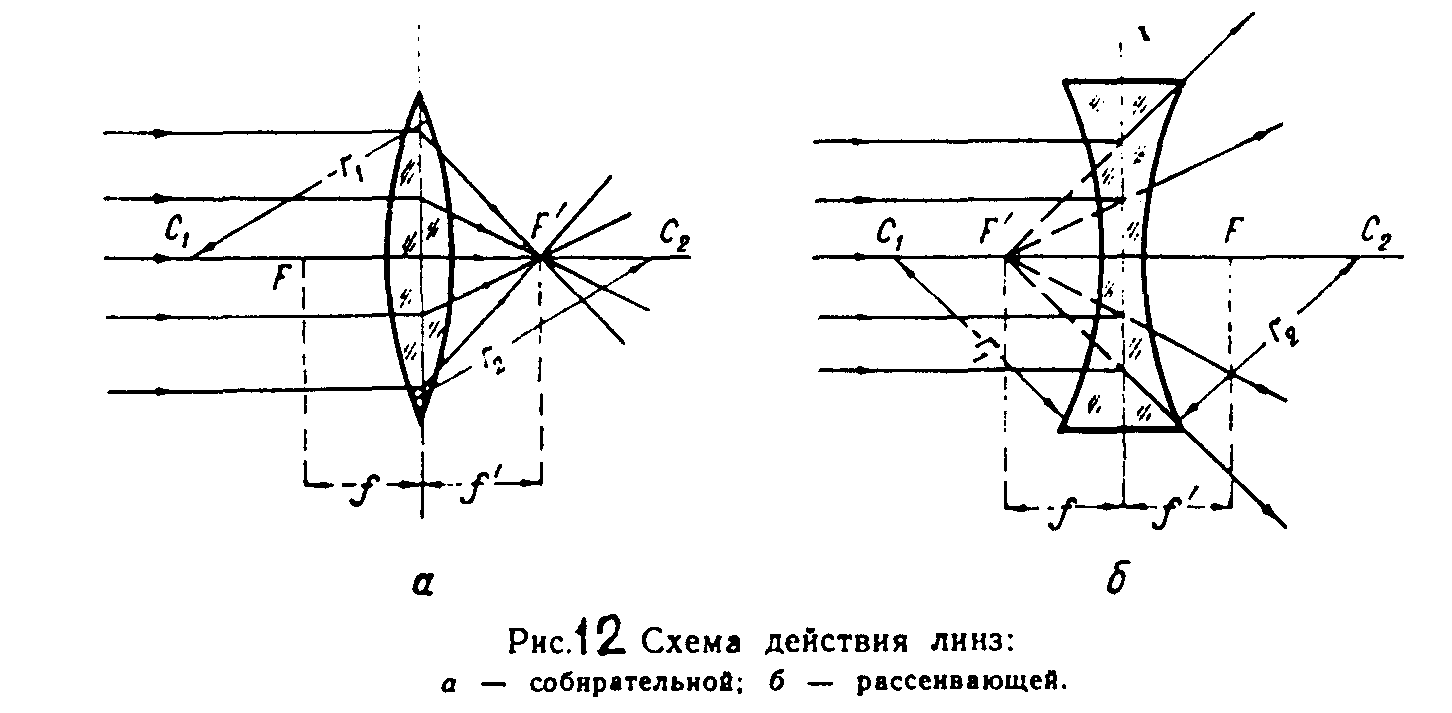
Рис.10. Схема действия линз:

а – собирательной; б – рассеивающей.

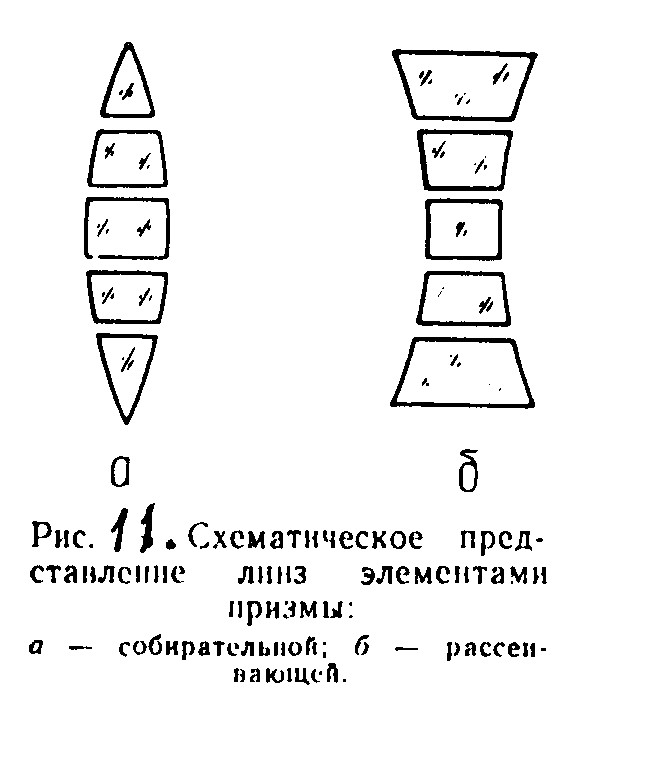
Рис. 11. Схематическое представление линз элементами призмы:

а – собирательной; б - рассеивающей