2.2. Плоскопараллельная пластинка

Плоскопараллельная пластинка – прозрачное тело, ограниченное двумя взаимно параллельными отшлифованными плоскостями.

П усть луч S составляет с нормалью к грани плоскопараллельной пластинки в точке падения N угол i₁ (рис.6). После преломления на границе «воздух - стекло» он пойдет по направлению NN₁ под углом i΄₁ к нормали и, вновь преломившись в точке N₁ на границе «стекло – воздух», получит направление N₁ S₁, составив с нормалью угол i_2. Ход луча подчиняется закону преломления

n₀ sin i₁ = n sin i΄₁ (11)

n sin i₂ = n₀ sin i΄₂

Напомним, что для воздуха показатель преломления n₀ принимается равным единице. Любые нормали к шлифованным плоскостям плоскопараллельной пластинки, в том числе и нормали в точках N и N΄, показанные на рис.8 пунктирными линиями, параллельны между собой. Поэтому i΄₁= i₂. Следовательно, на основании уравнений (11) имеем

sin i₁ = sin i΄₂;

i₁ = i΄₂ (12)

Последнее означает, что выходящий луч S₁ параллелен входящему лучу S, но смещен относительно него на величину h. Определим смещение h. Из прямоугольного треугольника NN₁O

(13)

Первое равенство системы (11) запишем следующим образом:

. (14)

Поскольку углы i₁, i΄₁ и (i ₁- i΄₁) - малые, толщину пластинки d примем равной отрезку NN₁, а синусы этих углов – самим углам в радианной мере. Тогда выражения (13) и (14) примут вид

; . (15)

Образуем из равенства (15) производную пропорцию

. (16)

Исходя из формулы (16)

. (17)

Подставляя значения разности ( i ₁- i΄₁) из уравнения (17) в (15) окончательно получаем

. (18)

Отсюда следует, что для одной и той же пластинки (d и n - постоянны) смещение луча h прямо пропорционально углу поворота пластинки i ₁. Свойство плоскопараллельной пластинки смещать лучи, оставляя их параллельными начальным направлениям, обуславливает ее применение в оптических микрометрах теодолитов, нивелиров и других приборов.

Рис.6. Ход луча через плоскопараллельную пластинку

2.3. Призмы

Различают призмы: преломляющие и полного внутреннего от­ражения. Преломляющая призма — прозрачное тело, ог­раниченное двумя полированными пересекающимися под некото­рым углом α плоскими гранями.

Призмы полного внутреннего отражения — прозрачные многогранники с полированными гранями.

Рассмотрим вначале преломляющие призмы.

Линию пересечения граней таких призм называют прелом­ляющим ребром, а угол пересечения — преломляю­щим углом (рис. 7). Преломляющую призму с малым прелом­ляющим углом (α ≤6°) называют оптическим клином. Луч S попадает на грань стеклянной призмы с показателем прелом­ления n в точке N. Углы падения и преломления соответственно i₁ и i΄₁. В призме луч идет по направлению NN₁, а далее попадает в воздух, преломившись на грани в точке N₁. Пусть углы падения и преломления в точке N₁ равны соответственно i₂ и i΄₂. Необходи­мо определить угол ε между начальным направлением луча SN и новым направлением луча N₁S΄, т. е, угол отклонения луча приз­мой. В треугольнике NAN₁ угол ANN₁, = i ₁- i΄₁ , а угол AN₁N = i΄₂- i₂. Угол ε — внешний угол треугольника NAN₁, он равен сумме не смежных с ним углов (i ₁- i΄₁) и (i ₁- i΄₁), т. е.

ε = i₁ - i΄₁ + i΄₂- i₂. (19)

В соответствии с законом преломления имеем

n₀ sin i₁ = n sin i΄₁ ; n₀ sin i΄₂ = n sin i_2. (20)

Так как углы падения и преломления в точках N и N₁ малы, а показатель преломления воздуха n₀ =1, то выражение (20) можно переписать в виде

i₁ = n i΄₁ ; i΄₂ = n i_2. (21)

Подставляя значения i₁ и i΄₂ из выражения (21) в (19), получаем

ε =(n-i) (i΄₁ + i₂) (22)

Угол между нормалями и гранями, пересекающимися в точке В, равен углу между гранями, т. е. α. Угол α — внешний угол тре­угольника NN₁B, поэтому α = i΄₁ + i₂. Учитывая это, запишем окон­чательно (22)

ε =(n-i) α. (23)

Как видим, угол отклонения луча призмой зависит от пока­зателя преломления материала, из которого изготовлена призма, и значения преломляющего угла. Напомним, что при прохожде­нии через призму луч разлагается на составные части спектра. Поэтому, чтобы сохранить резкость изображения предметов, рас­сматриваемых через призмы или клинья, необходимо создавать ахроматические призмы и клинья. Ахроматический клин состоит, как правило, из двух клиньев, изготовленных из разных сортов стекла и склеенных так, чтобы их преломляющие углы были обращены в противоположные стороны (рис. 7, б). Ахроматический клин отклоняет луч к основанию на угол ε, не разлагая его на составные части спектра.

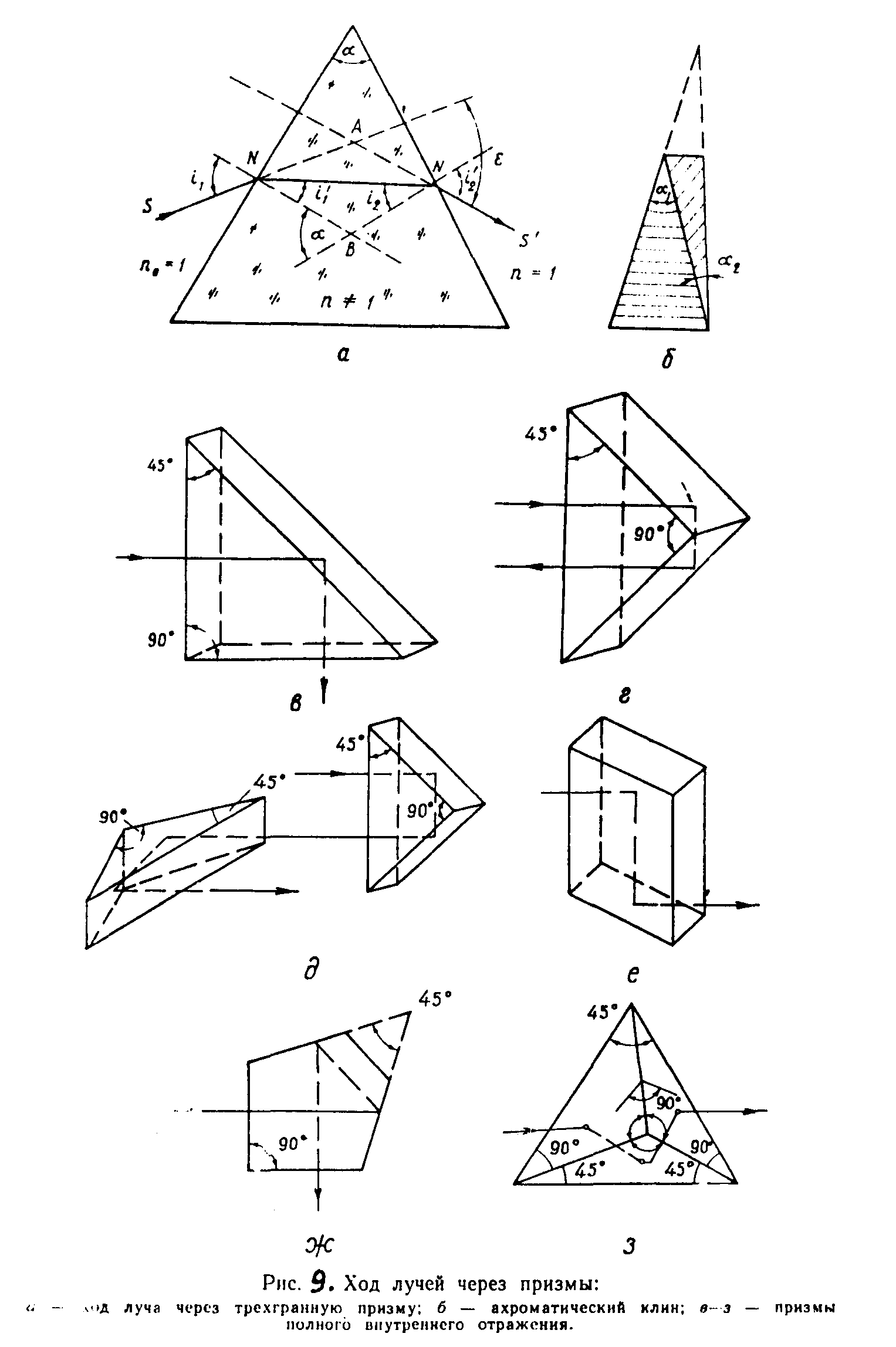
Рис.7. Ход лучей через призмы:

а – ход луча через трехгранную призму; б – ахроматический клин;

в – з – призмы полного внутреннего отражения

Рассмотрим призмы полного внутреннего отражения, для чего обратимся к рис.7, а и представим, что луч идет от точки N₁ к N. Тогда угол падения луча будет i΄₁ , а угол преломления - i₁ , причем i ₁- i΄₁, так как n₀< n . В случае постепенного увеличения угла падения i΄₁ возрастает и угол i₁, достигая при некотором критическом угле i΄₁ 90º. При этом условии, как и во всех случаях, когда угол i΄₁ больше критического, преломленный луч не наблюдается, и весь свет полностью отражается обратно в первую сре­ду. Такое явление носит название полного внутреннего отражения. Для усиления эффекта отражения отражающие грани иногда серебрят.

Наиболее распространены следующие призмы полного внут­реннего отражения:

1) трехгранная призма — дает такое же изображение как одно зеркало, если отражает гипотенузная грань (рис.7, в), если же отражение происходит от граней катетов (рис. 7, г), призма работает как система двух зеркал с углом между ними в 90°. При отражении от гипотенузной грани в случае поворота призмы на некоторый угол вокруг ребра с прямым углом, луч повернется на двойной угол (как при повороте зеркала), при отражении от гра­ней — катетов — поворот призмы не изменяет направления луча, так как происходит компенсация действия двух отражающих гра­ней;

2) система призм Поро I рода (рис. 7, д) — состоит из двух трехгранных прямоугольных призм, ребра, с прямыми углами которых взаимно перпендикулярны. Система поворачивает изоб­ражение на 180°, применяется в биноклях;

3) ромбическая призма (нормальные сечения такой призмы — ромб) (рис. 7, е) — смещает лучи, не изменяя их направление как плоскопараллельная пластинка;

4) пентапризма (рис.7, ж) — пятиугольная призма, продолже­ние двух граней которой пересекается под углом 45°. Дает эффект системы двух зеркал, установленных под углом 45°, т. е. двухзеркального экера, — изменяет направление луча на 90°;

5) крышеобразная призма (рис. 7, з) — имеет форму тетраэд­ра с углами между ребрами 90° и 45°. Дает полное обращение изображения, т. е. поворачивает его на 180°. Используется в оп­тических микроскопах, компенсаторах нивелиров, оптических ка­либровочных линиях светодальномеров и т. п.