§2. Основные сведения из геометрической оптики

2.1. Плоские зеркала

Тела из прозрачного или непрозрачного материала с гладкой шлифованной поверхностью называют зеркалами.

Одна из наиболее простых оптических систем — плоское зеркало, способное строить стигматическое изображение точки, как угодно расположенной в пространстве перед ним.

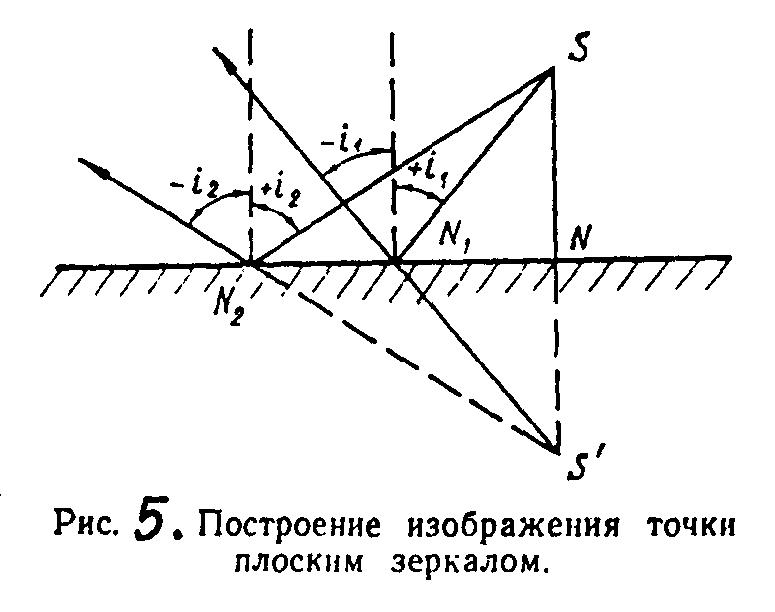
Рис.3. Построение изображения точки плоским зеркалом

Пусть на зеркало NN₁N₂ (рис. 3) падает гомоцентрический пучок лучей с центром в точке S. Так как лучи падают на зеркало под разными углами, то после отражения они удаляются один от другого. При этом глазу кажется, что они исходят из точки S' т. е. образуют новый гомоцентрический пучок с центром в точке S', расположенный на продолжении нормали SN к плоскости зеркала, причем S'N=SN. Следовательно, S' — стигматическое изо­бражение точки S. Это изображение будет лишь кажущимся — мнимым — и к тому же полуобращенным, поскольку в нем направление только одного из лучей изменится на противополож­ное.

Рассмотрим далее зависимость между поворотами зеркала и отраженного луча.

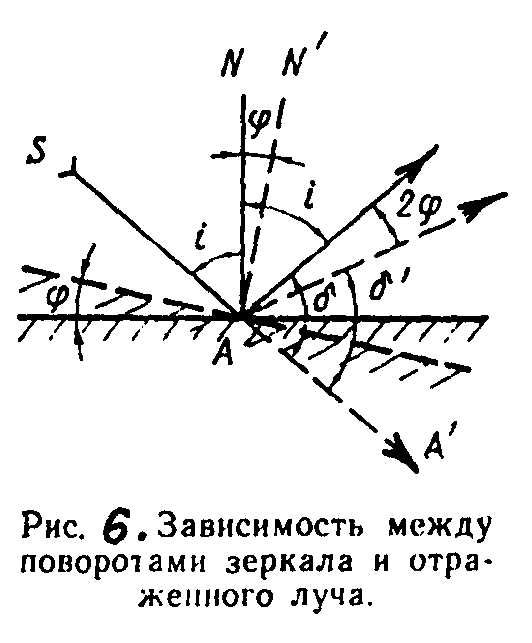
Рис.4. Зависимость между поворотами зеркала и

отраженного луча

Пусть световой луч S (рис. 4) падает на плос­кое зеркало в точке А под некоторым углом i и под таким же углом отражается. Отклонение отраженного луча от первона­чального направления (А А') составляет угол δ. На основании рис. 4 можно записать, что

δ = 180°–2i. (1)

Если повернуть зеркало вокруг точки А на произвольный угол φ, то нормаль N повернется на угол φ и займет положение N'A. От­раженный луч также повернется, причем его отклонение от перво­начального AА' составит теперь угол δ', который, согласно уравне­нию (1), запишем в виде

δ' = 180°–2(i + φ), (2)

Как видно из рис. 4, разность (δ – δ') дает искомое изменение направления отраженного .луча при повороте зеркала::

δ – δ' = (180°–2i) – [180°–2(i +φ)], (3)

δ – δ' = 2φ (4)

Следовательно, при повороте зеркала на угол φ отраженный луч повернется на угол 2φ. Это свойство плоского зеркала используется в геодезическом приборостроении, например в компенсаторах наклона.

Рассмотрим отражение луча SN от двух параллельных зеркал N и N₁ (рис.5). Нормали NE и N₁А к зеркалам параллельны и по­этому углы падения и отражения луча в точках N и N₁ будут равны i_1. В результате луч N₁S₁ будет параллелен лучу NS, но окажется смещенным на величину l = NB. Если расстояние между зеркалами N и N₁ равно h = АN₁, то из треугольника NN₁ А

N N₁ = h / cos i_1, (5)

а из треугольника NN₁ B

l = NB = NN₁ sin 2i_1. (6)

Подставляя выражение (5) в формулу (6) получим

l =2h sin i_1. (7)

Допустим, что плоскость зер­кала N₁D составляет с плоскостью ,зеркала ND угол α. Луч SN, отразившись от зеркала ND, пойдет по направлению NN₁ и составит с нормалью N₁E угол падения i_2.

После отражения от зеркала N₁D он получит направление N₁S₂ и составит с нормалью угол отражения i_2.

Из треугольника NDN₁

α = 180º - (90º- i₁) - (90º- i₂) = i_{1 +} i_2. (8)

Из треугольника NN₁C находим, что внешний угол β у точки С

β = 2(i_{1 +} i₂). (9)

Сопоставляя выражения (8) и (9), получим

β = 2α. (10)

Величина угла β зависит только от угла α и не зависит от углов i₁ и i₂. Поэтому при повороте обоих зеркал как системы угол β остается неизменным. Это свойство используется, например, в двухзеркальном эккере.

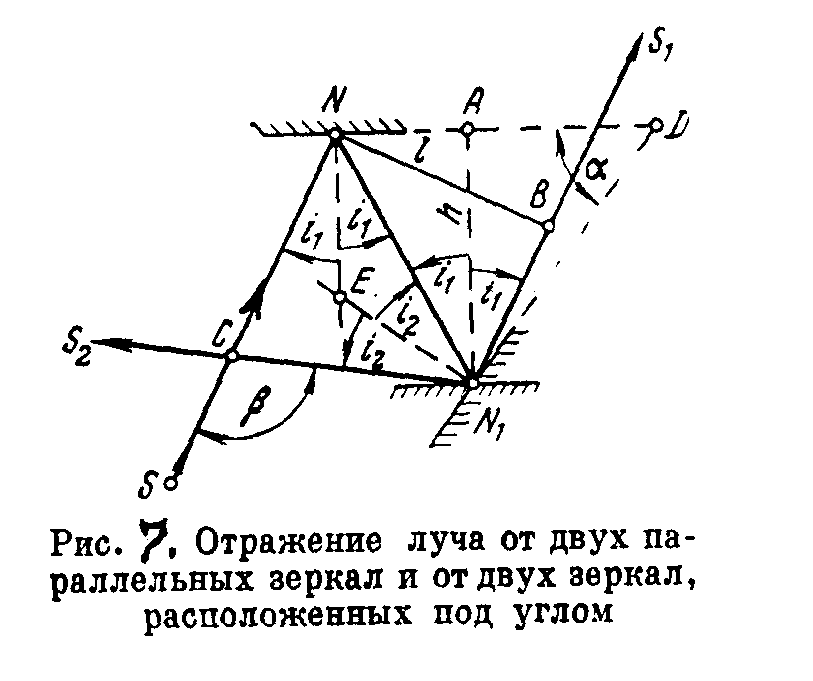
Рис. 5. Отражение луча от двух параллельных зеркал и от двух

зеркал, расположенных под углом