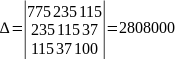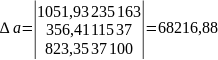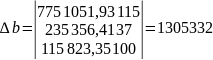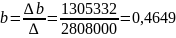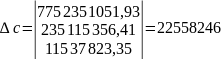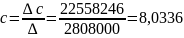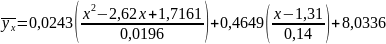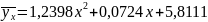Розділ іх.

Існують декілька типів залежностей між двома групами значень Х та У.

Якщо кожному значенню Х відповідає одне значення У, то між цими величинами існує функціональна залежність (тобто звичайна функція, котру вивчають ще в школі). Якщо ж кожному значенню величини Х відповідає деякий статистичний розподіл значень величини У, то між цими величинами є статистична залежність. В цьому випадку необхідно знайти середнє значення величини У для кожного значення величини Х.

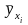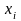Умовним середнім називається середнє значення величини У, які відповідають значенню величини Х.

.

Звісно, для кожного значення Х умовне середнє буде в загальному випадку різним, тобто умовне середнє є функцією від Х

.

В даній роботі знаходяться три регресії: лінійна, обернена та квадратична. Рівняння прямої лінії регресії має вигляд

,

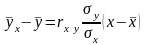y_x=3,61x+3,32

де r_xy – коефіцієнт кореляції, σ_x та σ_y – середні квадратичні відхилення, 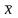та - вибіркові середні.

Рівняння оберненої лінії регресії має вигляд

,

де параметри a і b визначаються з системи рівнянь

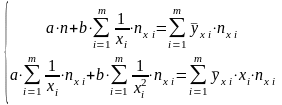
у_х1=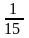 (5,45×2+6,75×5+8,05×3+9,35×3+11,95×1)=8,05

у_х2= (5,45×7+6,75×15+8,05×14+9,35×12+10,65×1+11,95×1)=7,74

у_х3= (5,45×3+6,75×1+8,05×8+9,35×6+10,65×2+11,95×3)=8,73

у_х4= (6,75×2+9,35×3+10,65×2+11,95×2)=9,64

у_х5= (9,35×1)=9,35

у_х6=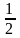 (6,75×1+11,95×1)=9,35

Х	1,17	1,31	1,45	1,59	1,73	1,87
ух	8,05	7,74	8,73	9,64	9,35	9,35
nx	15	50	23	9	1	2

x	yx	nx	nx/x	nx/x2	nx× yx	nx× yx/x
1,17	8,05	15	12,82	10,95	120,75	103,21
1,31	7,74	50	38,17	29,07	387	295,42
1,45	8,73	23	15,86	10,95	200,79	138,48
1,59	9,64	9	5,66	3,56	86,76	54,57
1,73	9,35	1	0,55	0,3	9,35	5,40
1,87	9,35	2	1,07	0,57	18,7	10
		100	74,13	55,43	823,35	607,08

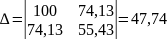
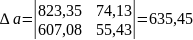
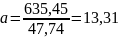
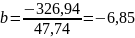
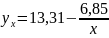
Для квадратичної регресії 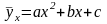аналогічна система рівнянь має такий вигляд:

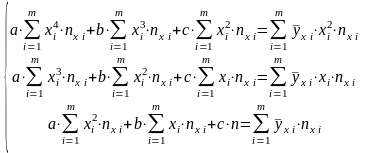
Розв’язуються рівняння будь-яким способом, наприклад, за формулами Крамера.

Якщо значення х_і незручні для обчислення, можна перейти до умовних варіант . Знайшовши рівняння квадратичної лінії регресії для величин u та y , після зворотної підстановки отримаємо шукане рівняння.

u	n		nu	nu2	nu3	nu4	n	n u	n u2
-1	15	8,05	-15	15	-15	15	120,75	-120,75	120,75
0	50	7,74	0	0	0	0	387	0	0
1	23	8,73	23	23	23	23	200,79	200,79	200,79
2	9	9,64	18	36	72	144	86,76	173,52	347,04
3	1	9,35	3	9	27	81	9,35	28,05	84,15
4	2	9,35	8	2	128	512	18,7	74,8	299,2
	100		37	115	235	775	823,35	356,41	1051,93