Розділ IV. Основні числові характеристики статистичного розподілу це:

Вибіркове середнє

, де - об’єм вибірки.

Дисперсія

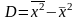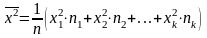, де та

Середнє квадратичне відхилення

.

Дисперсія та середнє квадратичне відхилення характеризують розсіяння значень відносно середнього.

Для зручності обчислень доцільно перейти до умовних варіант за формулою

, де h крок, якщо він є, а С – хибний нуль. В якості хибного нуля береться, як правило, значення з найбільшою частотою.

Вибіркове середнє для Х:

Х	1,17	1,31	1,45	1,59	1,73	1,87
n	15	50	23	9	1	2

1. С=1,31

2. U=X-C

U	-0,14	0	0,14	0,28	0,42	0,56
n	15	50	23	9	1	2

3. h=0,14 V=(X-C)/h

V	-1	0	1	2	3	4
n	15	50	23	9	1	2

4. = (-15+0+23+18+3+8)= =

V2	1	0	1	4	9	16
n	15	50	23	9	1	2

= (15+0+23+36+9+32)= =1,15

D_v= - ²=1,15-0,14=1,01

σ_v= _v = =1,005

В умовних варіантах ці ж самі величини знаходяться набагато простіше, а зворотній перехід відбувається за формулами

, , .

×0,14+1,31=1,36

0,02×1,01=0,02

0,14×1,005=0,141

Вибіркове середнє для Y:

Y	5,45	6,75	8,05	9,35	10,65	11,95
n	12	24	25	25	5	9

1. С=8,05

2. U= Y-C

   U	-2,6	-1,3	0	1,3	2,6	3,9
   n	12	24	25	25	5	9

3. h=1,3 V=( Y-C)/6

   V	-2	-1	0	1	2	3
   n	12	24	25	25	5	9

4. = (-24-24+0+25+10+27)= =0,14

V2	4	1	0	1	4	9
n	12	24	25	25	5	9

= (48+24+0+25+20+81)= =1,98

D_v= - ²=1,98-0,02=1,96

σ_v= _v = =1,4

В умовних варіантах ці ж самі величини знаходяться набагато простіше, а зворотній перехід відбувається за формулами

, , .

0,14×1,3+8,05=8,23

1,69×1,96=3,31

1,3×1,4=1,82

Розділ V.

Існують два основних теоретичних моменти:

Початковий момент порядку l

та

Центральний момент порядку l

.

За допомогою моментів легко обчислюються не тільки основні, а й додаткові числові характеристики.

Вибіркове середнє ,

Дисперсія ,

Коефіцієнт асиметрії ,

Екцесс .

Коефіцієнт асиметрії показує наскільки розподіл симетричне відносно свого середнього значення, а екцесс – наскільки розподіл відрізняється від нормального з такими самими характеристиками.

При переході до умовних варіант коефіцієнт асиметрії та екцесс не змінюються.

Будь-який центральний момент можливо виразити через початкові

,

,

,

.

Тому спочатку знаходять початкові моменти потрібних порядків, а потім обчислюються центральні.

Обчислювати початкові моменти зручно за допомогою таблиці

n	u	nu	nu2	nu3	nu4	n(u+1)4
15	-1	-15	15	-15	15	0
50	0	0	0	0	0	50
23	1	23	23	23	23	368
9	2	18	36	72	144	729
1	3	3	9	27	81	256
2	4	8	32	128	512	1250
Σ=100		Σ=37	Σ=115	Σ=235	Σ=775	Σ=2653

Останній стовбець знаходиться для перевірки:

Σn(u+1)⁴= Σnu⁴+4 Σnu³+6 Σnu²+4 Σnu+ Σn=775+4×235+6×115+4×37+100=2653

Початкові моменти:

М₁= =0,37

М₂= =1,15

М₃= =2,35

М₄= =7,75

Центральні моменти:

m₂ = 1,15-0,14=1,01

m₃ = 2,35-3×0,37×1,15+2×0,05= 1,17

m₄ = 7,75-4×0,37× 2,35+6×1,15×0,14+3×0,019=5,23

Коефіцієнт асиметрії:

= 1,16

Екцесс:

= 2,1304