Упражнение 1 Определение линейных размеров предметов

Измерение линейных размеров предметов осуществляется при помощи окулярного микрометра-масштаба, нанесенного на круглую стеклянную пластинку, помещенную между линзами окуляра, или перекрестия, которое может перемещаться при вращении микрометрического винта. Цена деления окулярного микрометра зависит от увеличения микроскопа и определяется при помощи объект-микрометра с известным масштабом.

Упражнение состоит в определении цены деления окулярного микрометра и измерение диаметра проволоки.

Упражнение 2 Измерение показателя преломления прозрачной пластинки

Рассмотренные ниже способы определения коэффициента преломления прозрачной пластинки с помощью микроскопа обусловлены явлением приближения предмета к наблюдателю, если предмет рассматривается через прозрачную среду (прозрачную пластинку), а, в конечном счете, явлением преломления света на границе двух сред.

Способ 1. Пусть на столике микроскопа лежит плоскопараллельная, прозрачная пластинка, например, стеклянная, толщиной , и микроскоп сфокусирован на метке или пылинке, находящейся на ее верхней поверхности в положении I. Чтобы увидеть в микроскоп нижнюю поверхность пластины следует опустить тубус микроскопа на расстояние (см. рис. 3.1) в положение II.

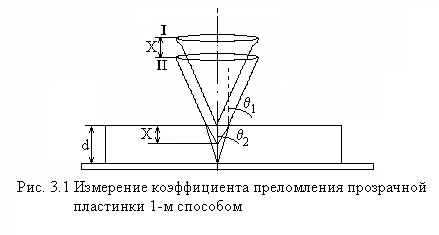
Рассмотрим ход лучей в данном случае. Из рис. 3.1 следу­ет:

. (3.2)

Из выражения 3.2, ограничиваясь малыми углами наблю­дения, получаем для коэффициента преломления исследуемой прозрачной среды:

. (3.4)

Выражение 3.3 справедливо лишь при использовании объектов с малой апертурой. Апертурой называется величина , где - угловая апертура объектива.

Способ 2. Пусть микроскоп сфокусирован на метку, которая находится на предметном стекле микроскопа – положение I. Если теперь положить на это стекло прозрачную пластину толщиной , то для фокусировки микроскопа на ту же метку, его тубус необходимо переместить вверх на некоторое расстояние (см. рис. 3.2) – положение II.

Ограничиваясь малыми углами, найдем значение . Используя соотношение (3.3), определим коэффициент преломле­ния исследуемой пластинки следующим образом:

. (3.5)

Способ 3. Если для одной и той же прозрачной пластинки поставить опыты в соответствии со способами 1 и 2, то коэффициент преломления этой пластинки можно вычислить по следующей формуле:

. (3.6)

В упражнении 3 используются пластинки с разными толщинами и показателями преломления. Для определения необходимо измерить их и в соответствии со способами 1, 2 и 3.

Контрольные вопросы и задания

1. Каковы основные причины систематических и случайных погрешностей в данной работе?

2. Почему у микроскопа, используемого в данной работе, увеличение окуляра больше увеличения объектива?

3. Как глубина резкости микроскопа влияет на точность измерений?

4. Получите формулу для определения показателя преломления при использовании объектива с большей апертурой, когда приближение (3.3) не выполняется.

ЛАБОРАТОРНАЯ РАБОТА № 4.

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ И СРЕДНЕЙ

ДИСПЕРСИИ ЖИДКОСТИ С ПОМОЩЬЮ РЕФРАКТОМЕТРА

ТИПА АББЕ (ИРФ-22)

1. Принцип работы рефрактометра типа Аббе

Рефрактометр - это прибор для измерения показателя преломления n (коэффициент рефракции) вещества в различных агрегатных состояниях. Основными методами рефрактометрии являются: 1) методы простого измерения углов преломления света при прохождении им границы раздела двух сред; 2) метод, основанный на использовании явления полного внутреннего отражения (ПВО) света или предельного угла; 3) интерференционные методы.

Рассмотрим физические принципы первых двух методов определения коэффициентов преломления. Третий метод подробно будет рассматриваться в 7-й лабораторной работе настоящего практикума по оптике.

Для измерения первым методом из исследуемого материла, находящегося в твердом состоянии, делают призму с преломляющим углом . Поворотом призмы (подбором угла падения луча на призму) добиваются минимального отклонения этого луча (угла ) от его первоначального направления. Для определения коэффициента преломления из геометрических построений и законов преломления можно записать следующее соотношение:

. (4.1)

Студентам рекомендуется самостоятельно разобраться с выводом формулы (4.1), с которой они будут встречаться при выполнении последующих работ настоящего практикума.

При использовании предельного угла преломления для измерения n исследуемого вещества (2-й метод) образец приводится в оптический контакт с эталонной призмой, обладающей высоким и точно известным коэффициентом преломления N (см. рис. 4.1). Луч, распространяющийся в исследуемом образце параллельно границе раздела, войдет в измерительную призму под предельным углом . а выйдет из нее под углом относительно нормали к поверхности ВС. Используя закон преломления и геометрию (см. рис. 4.1), можно записать следующие соотношения:

, (4.2)

где угол - угол при вершине измерительной призмы.

Студентам предлагается самостоятельно получить соотношения (4.2) и на их основе формулу:

, (4.3)

 

которая определяет связь коэффициента преломления с углами   ,  и коэффициентом преломления измерительной призмы N.

Существуют два типа рефрактометро в, которые используют метод предельного угла: это рефрактометры Пульфриха и Аббе. В настоящей работе используется рефрактометр ИРФ-22, который относится к рефрактометрам Аббе, поэтому мы подробно остановимся на основных моментах работы этого прибора.

Рефрактометр Аббе состоит из трех основных элементов: призменного блока Аббе; компенсатора дисперсии на основе двух призм Амичи; зрительной трубы. Рефрактометры этого типа имеют свои особенности: устройство измерительной ячейки; использование «белого» (дневного или искусственного) света; конструкция отсчетной шкалы, с устройством которой можно знакомиться в описании прибора.

Призменный блок Аббе состоит из двух призм: 1-я призма - измерительная, изготовленная из тяжелого флинта с преломляющим углом   ; 2-я - осветительная призма, изготовленная из любого стекла, имеет матовую поверхность А’В’ (см. рис. 4.2). Пространство между этими поверхностями (AB и A’B’) заполнено тонким слоем (0.1- 0.2 мм.) исследуемой жидкости. Поверхность А’В’ обеспечивает рассеянный свет, который через исследуемую жидкость падает на границу AB измерительной призмы. Можно считать, что на границу AB лучи свет падают под всеми углами, вплоть до максимального - . Строго говоря, из-за конечной толщины жидкости между призмами, максимальный угол падения на призму не будет равен , что приводит к определенной систематической погрешности определения по формуле (4.3).

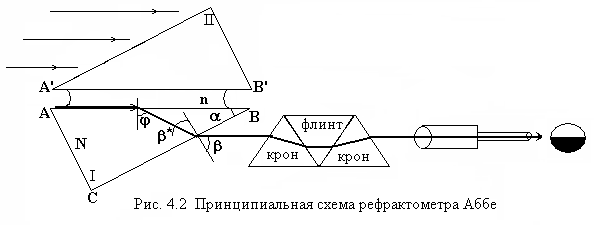
Использование призменного блока Аббе в рефрактометре позволяет производить измерения в проходящем и в отраженном свете. Это обстоятельство обуславливает возможность использования рефрактометра Аббе для исследования жидких и твердых веществ. Формула (4.3) получена в предположении, что наблюдаемые лучи входят в измерительную призму под предельным углом. В реальном приборе они входят под углами меньшими предельного, соответственно, выходя из измерительной призмы, лучи будут распространяться под углами меньшими . Для измерения угла в используется зрительная труба, в фокальной плоскости объектива которой собираются параллельные лучи, а с помощью окуляра рассматривается фокальная плоскость объектива. Поскольку при углах лучи не рассматриваются, то в соответствующей им области на фокальной плоскости будет темно, тогда как при - светло, то есть при наблюдается граница света и тени.

В рефрактометре Аббе в качестве источника освещения используют «белый» свет, что определяет появление радужных полос на границе света и тени (в области определенного угла). Это явление связано с наличием дисперсии измерительной призмы и исследуемого вещества, которая приводит к зависимости предельного угла от длины волны падающего света. Следовательно, угловая дисперсия исходящих из призменного блока Аббе граничных лучей F (голубой) и C (красный) связан с дисперсией вещества  и призмы   , здесь F, C и D (см. ниже) – фраунгоферовы линии ( , и ). Эта связь получается путем дифференцирования и комбинацией соотношений (4.2) и определяется следующим выражением:

. (4.4)

Для устранения этого явления и фактического определения дисперсии исследуемого вещества служит компенсатор дисперсии, состоящий из двух призм прямого видения - призма Амичи (рис. 4.3).

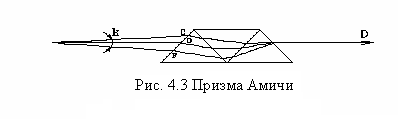
Эта призма склеена из трех: двух крайних из крона и средней из флинта. Углы и показатели преломления этих трех призм подобраны так, что лучи света определенной длины волны (обычно желтой линии D) проходили через систему без отклонения, в то время как лучи красной и фиолетовой части спектра отклоняются в противоположные стороны на различные углы в зависимости от длины волны. Если угловая дисперсия призмы Амичи подобрана такой, что она равна по значению и противоположна по знаку угловой дисперсии призменного блока Аббе с веществом, то суммарная дисперсия будет равна нулю, и размытие границы света и тени исчезает, причем положение четкой границы света и тени в этом случае совпадает с положением предельного угла для спектральной линии D, несмотря на то, что измерения производились в «белом» свете. Для расширения диапазона компенсации дисперсии используют блок из двух призм Амичи. Конструкция такого блока позволяет при повороте этих призм вокруг на угол  изменять его дисперсию от 0 до в соответствии с выражением:

. (4.5)

Найдем связь дисперсии вещества с угловой дисперсией   и некоторыми параметрами рефрактометра. В соответствии с (4.4) мы запишем соотношение:

. (4.6)

Выражая и через N и с учетом (4.5), перепишем соотношение (4.6) перепишется в следующем виде:

, (4.7)

где введены обозначения:

(4.8)

Мерой дисперсии служит поворот одной призмы компенсатора относительно другой до полного устранения окрашенности границы раздела. Отсчет производят по барабану разделенному на 120 частей. При повороте барабана на 180º (60 делений) дисперсия компенсатора пройдет все значения от нуля до двойного значения дисперсии одной призмы. Следовательно, если устранить окрашенность границы раздела и вращать компенсатор в ту же сторону до противоположного, но равного значения отсчета, то граница раздела вторично получится бесцветной.

Важной оптической характеристикой стекол является коэффициент Аббе:

. (4.9)

Для определения хроматической аберрации используется комбинация положительной и отрицательной линз. В простейшем случае, когда аберрация устраняется на краях спектра (для C и F линий), необходимо выполнить условие:

, (4.10)

где - фокусное расстояние положительной линзы, - отрицательной.

Студентам рекомендуется самостоятельно вывести формулу (4.10).

Измерив и , можно определить .