3. Порядок выполнения работы

Включите ртутную лампу (тумблер лампы ДРШ и кнопка «пуск» на блоке ЭПС-II, если ртутная лампа входит в комплект УМ-2). Установить ширину входной щели 0.05 мм и добейтесь четкого изображения желтого дублета, при этом регулировкой окуляра зрительной трубы добиться четкого изображения индекса (указателя в виде острия).

Упражнение 1 Способ измерения с помощью монохроматора

Вращая измерительный оцифрованный барабан и наблюдая в окуляр трубы, совместите измеряемую спектральную линию с остриём указателя, устанавливая его на середину изображения линии. По шкале измерительного барабана произведите отсчёт значения. Следует отметить, что при переходе к более коротким длинам волн необходимо подстраивать изменять положение объектива коллиматора, чтобы изображение осветительной шкалы оставалось чётким. Пройдя от желтой линии до фиолетовой, повторите измерения для тех же линий, но в обратном порядке, то есть от фиолетовой до жёлтой.

Упражнение 2 Построение градуировочной кривой

Для построения градуировочной кривой применяется интерполяционная формула Гартмана (10.5). С целью облегчения обработки результатов специально для этой лабораторной работы была написана не сложная программа, которая для трех пар значений вычисляет константы , строит график зависимости и определяет отклонения значений , вычисленных с помощью (10.5), от табличных. Последнее важно, так как позволит расставить «опорные» точки таким образо, чтобы обклонения были минимальными.

Особенностью программы является то, что следует подставлять в угловых градусах (непосредственно считываются по шкале барабана), а длину волны – в ангстремах (10 =1 нм).

По заданию преподавателя каждому студенту указывается неизвестная спектральная линия, для которой он должен определить длину волны, используя градуировочный график . Для решения этой задачи можно использовать ЭВМ или (10.5) с известными константами.

Воспользовавшись программой, определите для обоснованной выбранных трёх точек. Посторойте график зависимости , где - угол поворота призмы Аббе (в радианах). При построении следует иметь в виду, что поворот барабана на 2º (цена деления барабана) соответствует повороту призмы Аббе на 20˝.

Упражнение 3 Определение угловой дисперсии призмы

Используя результаты полученные в упражнении 2, найдем для различных длин волн. Построить график зависимости .

Контрольные вопросы и задания

1. Получите формулу (10.4) для дисперсии стеклянной призмы.

2. Пользуясь зависимостью найдите зависимость , полагая .

3. Из (10.4) оцените величину призмы, считая, что она изготовлена из оптического стекла марки ТФ-1. Оптические свойства стекла приведены в приложении Г.

4. В чём состоит преимущество интерполяционной формулы Гартмана перед другими?

5. Почему при переходе от одной спектральной линии к другой нужно каждый раз фокусировать коллиматор?

ЛАБОРАТОРНАЯ РАБОТА № 11

ИЗУЧЕНИЕ ВРАЩЕНИЯ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ И ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ САХАРНЫХ РАСТВОРОВ С ПОМОЩЬЮ САХАРИМЕТРА

1. Теория явления вращения плоскости поляризации

Феноменологическая теория вращения плоскости поляризации

Впервые в начале IXI столетия, это явление наблюдал Араго, исследуя прохождение линей­но поляризованного света вдоль оптической оси кварцевой пластинки (см. рис. 11.1). Эксперимен­тально установлено, что угол поворота плоскости поляризации зависит от толщины кварцевой пластинки следующим обра­зом:

, (11.1)

где - удельная вращательная способность кварца, зави­сящая от длины волны.

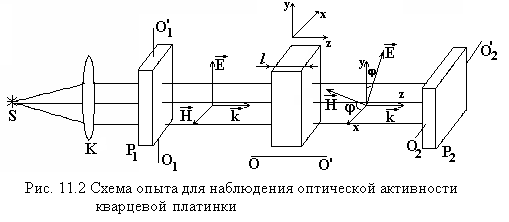
На рис. 11.1 приведены следующие обозначения: S - точечный источник, K - конденсор, Р₁ - поляризатор, Р₂ - анализатор, OO'- оптическая ось образца .

Исследование этого явления в кварце показывает, что удельная вращательная способность этого кристалла сильно зависит от спектральной области (так для красной области видимого спектра = 15 град/мм, для зеленой - ~ 27 град/мм, для фиолетовой - ~ 51 град/мм). Кроме этого установлено, что для пластинок, вырезанных из правого кварца, поворот плоскости поляризации происходит по часовой стрелке, а для пластин из левого кварца - против часовой стрелки. Угол поворота измеряется со стороны наблюдателя.

Позднее это явления было обнаружено в других кристаллических, аморфных, жидких и газообразных веществах (скипидар, раствор сахара, патока, камфара, никотин, теллур, селен, хлорид натрия и другие). Исследования данного явления в растворах, приведенных физиком Био, показали, что

, (11.2)

, (11.3)

где - удельная оптическая активность однопроцентного раствора, С - концентрация (в процентах) содержания вещества в растворе.

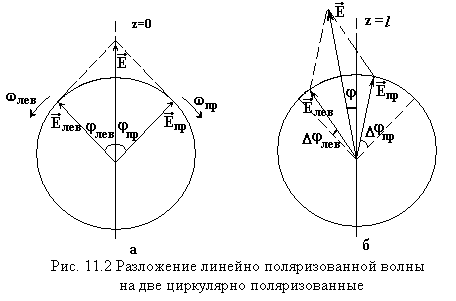
Объяснение оптической активности впервые было дано Френелем (1827). Согласно Френелю всякое линейное колебание можно разложить на два круговых колебания с правым и левым вращением, то есть линейнополяризованная волна является суперпозицией право – левоциркулярно поляризованных волн с , . В этом случае, если скорость циркулярно поляризованной волны зависит от направления вращения вектора , то плоскость поляризации поворачивается (см. рис. 11.2-б). Это явление называется круговым двойным лучепреломлением.

Найдем связь между углами поворота плоскости поляризации и , где - показатели преломления право- и левоциркулярно поляризованных волн.

Пусть в точке , , так что (см. рис. 11.2 а). В этот же момент времени в точке (ближе к наблюдателю):

,

(11.4)

.

Учитывая знаки углов и рис. 11.2-б из (11.4) получим:

. (11.5)

Поскольку , , где - длина волны в вакууме, то

. (11.6)

Из рис. 11.2 и формулы (11.6) следует, что плоскость поляризации поворачивается в туже сторону, в какую вращается вектор циркулярно поляризованной волн, распространяющейся с большей скоростью ( ).

Воспользовавшись тем, что , преобразуем к виду:

. (11.7)

Феноменологическая теория Френеля показывает наличие поворота плоскости поляризации при распространении линейно поляризованной волны в среде, в которой , но не объясняет причину этого явления.